Olikhet med absolutbelopp
Hej! Jag har problem med den här uppgiften:
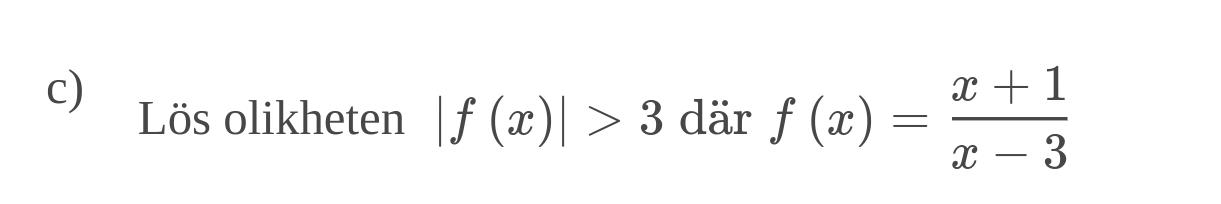
Jag tänkte såhär:

Men facit säger att rätt svar är 2<x<3 eller 3<x<5. 3 kommer ju ifrån att funktionen har en asymptot som är x = 3, men jag fattar inte varför jag får att x<2 istället för x>2. Det är ju lite konstigt att x<5 och x<2 samtidigt, så jag har ju gjort något fel, men jag fattar inte vad.
I fall 1 kommer du fram till att x<5. Detta under förutsättningen att absolutbeloppet är onödigt och uttrycket innanför tecknen blir positivt. Då kan du undersöka för vilka x som absolutbeloppstecknen är onödiga, för att se vilka ytterligare begränsningar på x som gäller i fall 1.
Samma resonemang på fall 2: vilka x gör så att absolutbeloppstecknen är nödvändiga?
Skulle man kunna rita lösningen?
| x+1 | är avståndet från x till -1 på tallinjen
| x-3 | är avståndet från x till 3 på tallinjen
För vilka tal x gäller då att | x+1 | är tre gånger så stort som | x-3 | ?
etc
Notera att om du har olikheten (x+1)/(x-3) > 3, så implicerar det att x+1 > 3(x-3) i det fall att x > 3 och att x+1 < 3(x-3) i det fall att x < 3.
Liknande resonemang gäller olikheten (x+1)/(x-3) < -3.
Följande axiom gäller för olikheter.
a < b och 0 < c implicerar att ac < bc.
En följd av detta är att a < b och c < 0 implicerar att bc < ac, eller om man så vill att ac > bc.
PATENTERAMERA skrev:Notera att om du har olikheten (x+1)/(x-3) > 3, så implicerar det att x+1 > 3(x-3) i det fall att x > 3 och att x+1 < 3(x-3) i det fall att x < 3.
Liknande resonemang gäller olikheten (x+1)/(x-3) < -3.
Följande axiom gäller för olikheter.
a < b och 0 < c implicerar att ac < bc.
En följd av detta är att a < b och c < 0 implicerar att bc < ac, eller om man så vill att ac > bc.
Okej, det förstår jag. Men hur kan jag använda mig av det nu?
För varje fall i din första lösning måste du dela upp två delfall: ett då x > 3 och ett då x < 3.
PATENTERAMERA skrev:För varje fall i din första lösning måste du dela upp två delfall: ett då x > 3 och ett då x < 3.
Jag är fattar inte riktigt hur jag gör det dock. Ska jag testa att sätta in olika värden?
Notera att om du har olikheten (x+1)/(x-3) > 3, så implicerar det att x+1 > 3(x-3) i det fall att x > 3 och att x+1 < 3(x-3) i det fall att x < 3.
Hänger inte med på hur man får fram x<3 heller. Gissar att det är på grund av asymptoten?
Du har olikheten (x+1)/(x-3) > 3. Du multiplicerar båda sidor med (x-3) och får x+1 > 3(x-3) . Notera nu att detta är sant bara om x-3 är större än noll, dvs om x > 3.
Om x-3 är mindre än noll (x < 3) så måste du vända på olikheten när du multiplicerar med x-3, dvs du skall då beakta olikheten x+1 < 3(x-3). Se #4.
Du måste således lösa olika olikheter beroende på om x > 3 eller x < 3.
När det gäller olikheten (x+1)/(x-3) < -3 så måste du på liknande sätt skilja på om x > 3 eller x< 3.
Klart?
Nu börjar det falla på plats! Jag gjorde så här:

(Vänster är (x+1)/(x-3) > 3 och höger är (x+1)/(x-3) < -3)
Då får jag ju både de rätta och de felaktiga svaren. Finns det något smart sätt att visa att de inte är relevanta, eller räcker det typ om man testar olika värden?
Notera att x kan inte vara mindre än 3 och samtidigt större än 5, så den andra olikheten från vänster uppfylls inte av något x. Ingen giltig lösning.
Samma sak gäller tredje olikheten. x kan inte vara samtidigt större än 3 och mindre än 2. Ingen giltig lösning.
Första och sista olikheten ger giltiga lösningar. 3 < x < 5 eller 2 < x < 3.
Just det, tack så mycket! :)
Ett alternativt sätt du kan göra det på är med en enkel omskrivning:
...
Enkelt sätt att slippa massa "fall" på. Intervallet du får blir då , men eftersom 3 inte är inkluderat måste du såklart dela upp det i två intervall:



