Onödig mängd geometri i gymnasiet/högstadiet?

Fysik och praktisk problemlösning. Att kunna se mönster i problem man ställs inför som ingenjör. 

Det finns väldigt mycket kunskap som vi lär oss under vår tid i utbildningsväsendet som vi aldrig använder praktiskt. Att sen säga att det inte varit till någon nytta är inte rättvist, för det har onekligen tränat upp våra förmågor och ger oss en bred förståelse för världen omkring oss. 

För de som ska bestämma vad vi ska och inte ska lära oss är det en hopplös uppgift att göra en kursplan som precis bara lär ut det just du behöver under livet och inget annat. Vi måste inse att utbildningen ska vara till nytta för de flesta som går i skolan, ingen kommer att använda all kunskap, men all kunskap används av någon. Allt beror ju på vad vi gör med den kunskap som vi har. 

Jag kan utan vidare räkna upp massor med kurser och kunskaper från min utbildning till civilingenjör som jag aldrig använt yrkesmässigt, men att hävda att kunskapen och kurserna är onödiga, för mig eller alla andra, som gått samma linje är inte korrekt. De har tillsammans skapat en bred kunskapsbas som man står ganska tryggt på när man upptäcker att utvecklingen går fort framåt och man hela tiden måste lära sig nya saker för att hänga med. Vem kunde tro att kursen i maskinskrivning som var obligatorisk i min skola (1963) när jag var 13 år skulle visa sig ytterst värdefull för en framtida ingenjör?

Skulle vi göra skolåren smalare med avseende på kursinnehåll skulle vi tvingas välja yrkesinriktning mycket tidigare i livet, vilket inte är lätt, dessutom skulle vi ganska snart upptäcka att utvecklingen springer ifrån oss.

Jag vet inte om du missade min sista mening där men mja.

Min avsikt är inte att hata på mitt favoritämne här men det finns en hel del viktigare saker man inte hinner med i matteundervisningen upp till gymnasiet, jag ser då hellre att man tar bort dessa geometridelar och satsar på det som är viktigt på riktigt.

Man hinner tex inte alls med så mycket differentialekvationer upp till matte 4 (det finns i ma5 men är frivilligt), och ingenting om linjär algebra utom i matte specialisering vilket ännu färre har gått än matte5.

Sen var min fråga mer om någon faktiskt känner till en tillämpning av dessa satser, och om du nu insinuerar att någon kan ha användning av dessa så kan du gärna nämna vilka. Jag är alltså ganska säker på att man inte hör talas om dessa igen även om man går ett kandidatprogram i matematik.

Detta är off topic men jag är i övrigt emot idén om att motivera innehållsmässigt onödiga mattekurser med att man kan "träna logiskt/abstrakt/systematiskt tänkande". Jag gillar matte men ser på det pragmatiskt. Envariabelanalys på KTH är tex en kurs som alla civilingenjörsprogram läser, men som sett till innehållet inte är 100% relevant (kanske ~70%). Förmågorna man lär sig av högre matematik kan man likväl träna upp med hjälp av något annat ämne eller åtminstone nån annan mer relevant mattegren.

Vissa mattekurser tillhörande vissa program ges "in-house" dvs inte centralt av KTH:s matteinstitution utan av deras egna (biotekniks kurs i differentialekvaitoner ges av en biofysiker), den idén gillar jag starkt. Föreläsaren har möjlighet att specialgjuta kursen till studenternas behov, ge mycket mer relevanta exempel och levandegöra hela kalaset.

Tja, flera av dessa, framförallt de trigonometriska satserna, använder man redan i Fysik 2. Sedan kan det ju vara så att man använder saker som bygger på dessa satser.

Det är ju det som är matematikens problem, det är verktyget som vi använder för att förstå annat. Det är ju svårt att veta exakt vad du kommer att behöva i resten av din utbildning.

AndersW skrev:

Tja, flera av dessa, framförallt de trigonometriska satserna, använder man redan i Fysik 2.

Exempel?

Sedan kan det ju vara så att man använder saker som bygger på dessa satser.

Exempel?

Det är en intressant fråga vad som är relevant i undervisningen idag. Särskilt när vi ser att AI gör större och större framsteg. Jag utbildade mig till elkraftsingenjör på den då fyraåriga gymnasielinjen och fick en bra grund att stå på. Vi blev bra på att söka kunskap vid behov och att kunna använda färdiga formler. Ett litet förakt för civilingenjörer fanns på arbetsplatserna under min yrkestid. De ansågs opraktiska och hade ingen förståelse för de praktiska konsekvenserna var en ganska spridd åsikt inom pappersindustrin under senare hälften av 1900-talet. Att de var de och högt utbildade personer som lagt och lade grunden till hela vår tillvaro var något som många inte förstod.
Det blir väldigt tydligt för mig nu när jag börjat att lära mig lite grand om matematiken och fysiken på högskolenivån. Förståelsen av alla dessa formler vi lärde oss att använda i gymnasiet och som vi sedan använde i arbetslivet, kommer först på högskolenivån. De två böcker jag köpt Adams "Calculus" och Hallidays "Fundementals of Physics", två riktiga tegelstenar, som innehåller så mycket av det jag har förstått genom åren att jag saknat i min utbildning. Kanske framförallt efter 1980 då teknikutvecklingen inom industrin var enorm. Jag tänker då på all datateknik, motor och ventilstyrning. En helt ny värld som alla byggde på civilingenjörers och forskares kunskaper.
De sista åren i mitt arbetsliv anställdes en hel del ungdomar som hjälpte oss med stora ombyggnader av vår pappersfabrik. De gamla suckade och sa att de förstår ju inget av en industri som vår, men det visade sig vara helt fel. Tvärtom så blev de vår räddning och utan deras kunskaper vågar jag påstå att vi inte haft någon pappersfabrik kvar i Hallstavik idag. Naturligtvis behövdes vi gamlingar också, men utan ungdomarnas kunskaper hade vi inte klarat det.
Så i dagens industrier behövs nog många gånger de grundkunskaper vi får i gymnasiet och har vi även grunderna från högskolan så tror jag att vi kan höja ribban ytterligare på våra industrier.
Att utbildningen behöver moderniseras det är nog sant, men frågan är hur. Att ha en bra och bred grund att stå på är bra för de som arbetar i projekt inom den moderna industrin.

Cosinussatsen använde jag i Fysik 2. Minns inte exakt vad det handlade om, elektriska fält eller något liknande? Men det var självklart ingenting man använde hela tiden.Var kanske en enda uppgift. Utanför matte 3/4 så har jag nog inte använt någon av metoderna Q nämner. Det som varit mest användbart är likformighet, Pythagoras, trigonometri (sin,cos,tan.... osv) och sådant. Jag trodde dock Cosinussatsen var anvämdbar i fysik men kanske inte?

Men jag vet inte om jag tycker att man slösar mycket tid på att lära sig dessa satser. Jag tyckte inte man lade ner mycket tid på dessa alls men det kanske beror på lärosätt?

Sedan brukar ju geometri anses som väldigt elegant inom matematik så det kanske är en faktor? ;)

En gång i tiden gick man igenom Euklides' Elementa i matteundervisningen.

Laguna skrev:

En gång i tiden gick man igenom Euklides' Elementa i matteundervisningen.

Är inte det som när jag skojar med barn och barnbarn. "När jag gick i skolan var 7 x 8 = 56, men det kanske inte gäller nu längre?"
Lite så är det väl med Euklides Elementa också? En stor del är väl sanning än idag?

På gymnasiet används Sinus- och Cosinussatserna i fysik- och teknikämnen (som t.ex. hållfasthetslära, ellära) bland annat för att beräkna längder av krafter, hastigheter, rörelsemängder, strömmar och spänningar.

Exempel

En partikel har från början rörelsemängden $\mathbf{p}_1$. Efter en kollision uppmäts rörelsemängden $\mathbf{p}_2$. Bestäm förändringen (impulsen) $\Delta \mathbf{p}$  till storlek och riktning.

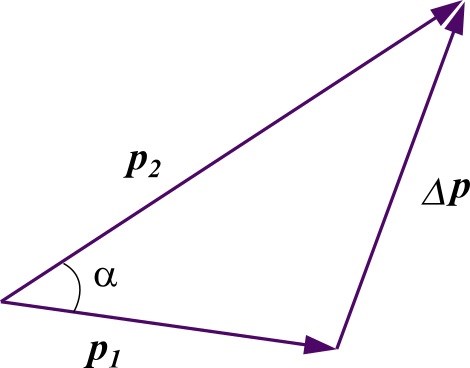
Ska jag vara ärlig stör jag mig mer på att jag var tvungen att lära mig att virka och sticka under syslöjden. Det har jag aldrig använt, varken under fortsatta studier, i mitt yrkesliv eller privat.

Däremot vann jag en gång en pubquiz genom att blixtsnabbt kunna svara på utslagsfrågan "Vad är knyppling". Så jag fick iaf gratis öl tack vare syslöjden.

Du kan göra stickning eller virkning till en hobby när som helst.

Jag har haft användning av sinussatsen och cosinussatsen många gånger när jag räknat mekanik, EMF samt inom fasta tillståndets fysik när vissa geometriska samband hos enhetsceller, gitter, dislokationer osv. ska härledas. 

Jag tycker det låter märkligt att du inte skulle gjort det då så många av Apazidis uppgifter bygger på sinussatsen och cosinussatsen. Alla punkter på din lista lär du dig för att de förenklar geometrisk analys. Du måste inte använda dem men cosinussatsen till exempel är mycket användbar och sparar tid istället för att gå en längre väg med ren trigonometri + pythagoras.

Hur gjorde du när du räknade mekanik på en uppgift som denna, exempelvis:

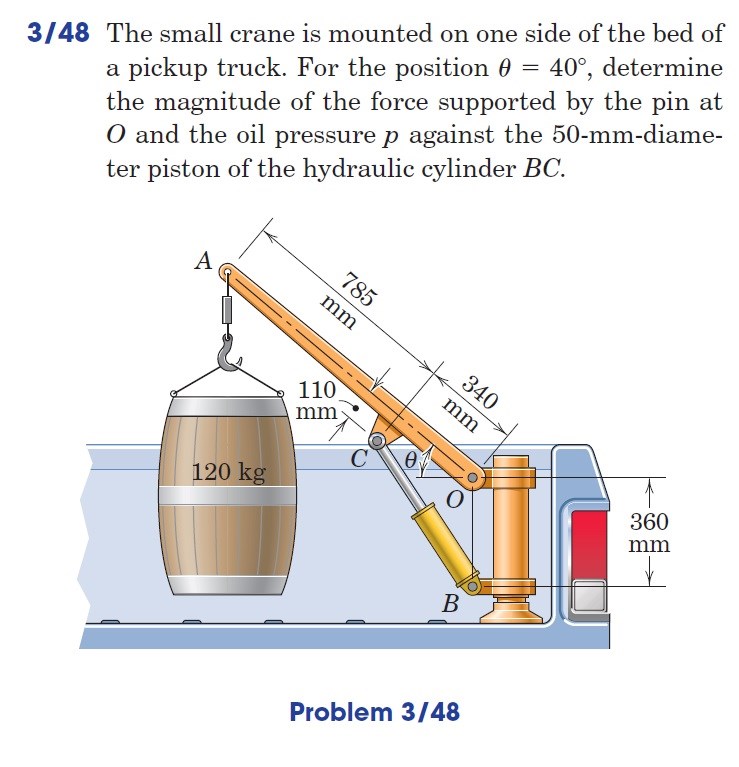
Man kan använda vektorer framgångsrikt men resultatet från detta kommer bara säga exakt samma sak som cosinussatsen så indirekt använder du den, egentligen.

Historiska skäl. Geometri i undervisning är en rest från Euklides där det ofta användes för att öva logik och satskonstruktion - principen om att resonera från definitioner och satser är i sig viktig. Från mitt perspektiv (som lärare med fritidsintresse av geometri) så är geometrin redan väldigt marginaliserad och reducerad. Det som återstår är i praktiken orientering om form och symmetri (att känna igen det som är likbent, att spetsigt skiljer sig från trubbigt osv), (potentiellt) praktiska metoder för att mäta avstånd (likformighet och pythagoras och trigonometri), och orientering i att föra resonemang där kedjor av enkla påståenden binds samman till slutsatser. Men mycket tid lägger man inte på dessa och vid varje undervisningsreform liten som stor blir det mindre och mindre geometriskt innehåll. 

Det sagt så ser trigonometrisk geometri ganska bred tillämpning. Det är inte alltid det kraftfullaste verktyget men då och då så snubblar man över situationer där sinussatsen plötsligen är användbar och det vore olyckligt om man var blind för möjligheten när den uppenbarar sig. (Eller rättare sagt om man inte kunde förstå sina äldre nä de använder dem)

På senare år har jag jag blivit intresserad av astronomi och där är trigonometrin och geometrin går hand i hand. Det är inte för intet att astronomins fader och trigonometrins fader är samma person. (Hipparchos)

Exempelvis är vinkeln mellan solen och Venus intressant då den påverkar hur långt bort från solen venus uppträder på himlen och till första approximation kan man jobba med en liten triangel där man vet två sidors längder, den mellanliggande vinkeln, och härleder resten .^^. 

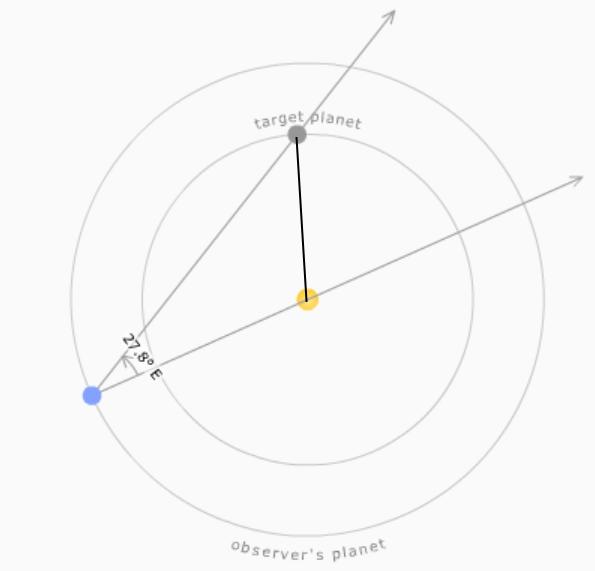
Sfärisk trigonometri, rotationsmatriser osv är kraftfullare verktyg för analys av himlarörelser men jag uppskattar att jag har koll på verktyg som tillåter mig att ofta göra en uppskattning

Jag tycker det låter märkligt att du inte skulle gjort det då så många av Apazidis uppgifter bygger på sinussatsen och cosinussatsen

Va? Nej, inget som helst minne av det? Om jag hade sett det skulle jag tyckt att det var konstigt och att han med flit gjirde det för att få oss att träna geometri. De flesta trianglar var räta.

Seriouscephalopod: jo, ja, symmetri, rotationer speglingar osv (som snuddar jättenära gruppteori) tycker jag är intressant och faktiskt användbart i alla fall för folk som ska plugga ingenjöriga program efter gymnasiet. För att få en bättre känsla och kunna tillämpa det på problem/integraler för att förenkla dem. Noethers sats tänker jag också på, symmetri i mer generell bemärkelse.

Jag är nog lite hård när jag skriver just cosinus och sinussatsen högst upp (jag skrev av från formelbladet från ma4 för jag minns inte ens vilka det var), för de är mest användbara i den listan. Ärligt talat är den enda trigonometriska formeln jag använt så mycket att jag minns är trigettan och cosiuns dubbelvinkel. Additions/subtraltionsformel skulle jag behöva kolla upp om jag behövde...

Amerikaner och deras relation till trigonometri är ännu skevare. De lär sig inte bara om alla sex trigfunktioner och har en kurs/modul tillägnad bara det, jag fattar inte det. Hur mycket finns det att lära sig om det?? Och hur den kallas en "gren" av matematiken låter så gammeldags.

Angående trianglar tycker jag det räcker att man känner till vad som ger en komplett information om den (tre sidor, tre vinklar+en sida, två sidor+en vinkel...), och det som saknas får man leta efter en formel för för den konkreta uppgiften.

Exempel? Till exempel detta från Heureka fysik2 kapitel 2:

c uppgiften kräver triangelsatserna.

Om man inte går igenom dessa blir hoppet ganska stort när man sedan börjar prata om trigonometri som periodiska funktioner och det används i stor utsträckning i Fysik, ellära osv.m Jag använder dessutom sinus och cosinussatsen för att bevisa sin (u+v) och cos (u+v). Dessa används sedan i elläran. I elläran används också komplexa tal och du förstår inte komplexa tal i polär form utan trigonometrin.

OK, jag kan hålla med om vissa satser, som randvinkelsatsen, har jag lite svårt att motivera. Det är nog mer en träning i logiskt tänkande.

Jag tycker dock att inställningen att man kan hitta en formel är inte alltid så fruktsam. Det märks på proven när eleven har desperat letat efter en formel i formelsamlingen som verkar passa de data man har. Det blir ofta inte helt rätt för att uttrycka det milt. Dessutom är detta om hitta det när man behöver det en konstig inställning, om man inte vet vad som finns vet man inte heller vad man letar efter. Jag jobbade ett tag på en skola som jobbade med PBL, problembaserat lärande. Där hade vi en gång ett projekt som krävde vissa trigonometriska samband, då bara i rätvinkliga trianglar, och tanken var ju att eleverna skull hitta denna del av matematiken. Det var inte en enda som gjorde det. Om man pekade ut det var reaktionen: Och?

Qetsiyah skrev:

[...]

[...]

Jag är nog lite hård när jag skriver just cosinus och sinussatsen högst upp (jag skrev av från formelbladet från ma4 för jag minns inte ens vilka det var), för de är mest användbara i den listan. Ärligt talat är den enda trigonometriska formeln jag använt så mycket att jag minns är trigettan och cosiuns dubbelvinkel. Additions/subtraltionsformel skulle jag behöva kolla upp om jag behövde... [...]

Trigonometri är ändå väldigt användbart som en metod för beräkning och om några av satserna kopplade trigonometri är mer användbara än andra så är det priset för att man ska ha en 

Håller egentligen endast med om att tre satser på listan är svårmotiverade.

• Kordasatsen
• Randvinkelsatsen
• Bisektrissatsen

Både som bevis och som del av geometriproblem är dessa väldigt trevliga och de används som modellexempel på bevis och som del i problemlösning -- men individuella som resultat är de för mig rätt opraktiska.

Eller rättare sagt. De är väldigt användbara för att geometriskt härleda eller motivera matematiska identiteter men de saknar direkta praktiska tillämpningar. Exempelvis kan $y = 2x$-sambandet i randvinkelsatsen tillsammans med likbenta trianglar användas för att härleda sinussatsen $\sin(2x) = 2 \sin(x) \cos(x)$ genom arean hos triangeln CDB i figuren nedan. (Randvinkelsatsen ger på liknande sätt ett extremt lätt bevis för sinussatsen.)

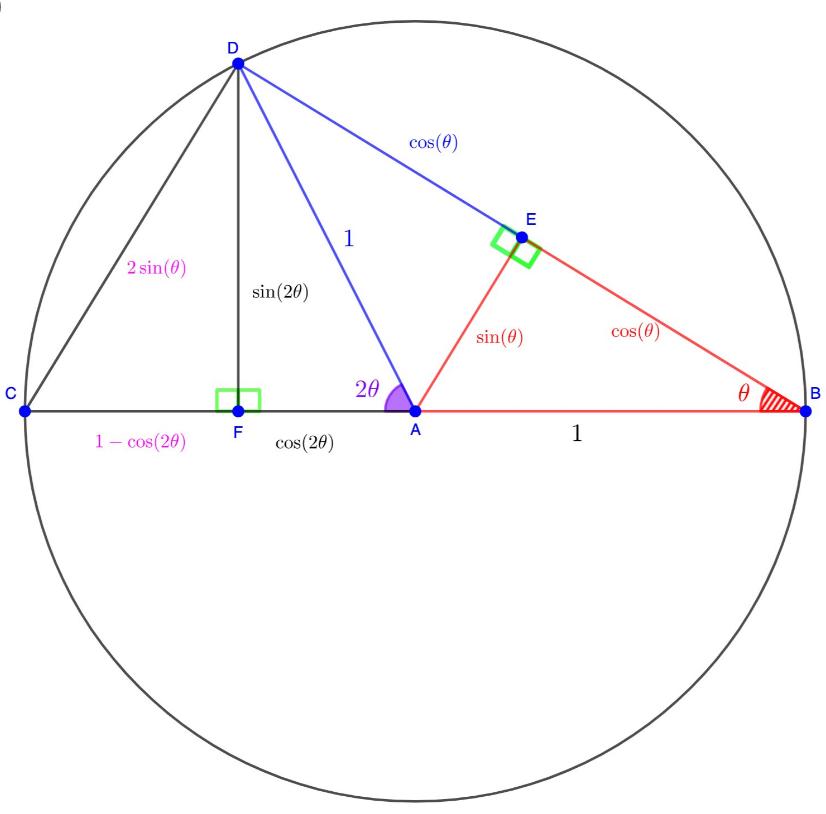
Utifall satserna faktiskt användes för att bevisa andra satser skulle de ha värde men som det är nu är de nästan en slags anakronismer. I slutändan är det rimligt att fokusera på det praktiskt tillämpbara i en allmänn skola.

Medan det finns en charm i tanken att man kan bli bättre på logiskt tänkande rent allmänt om man håller på med geometri så är det en idé jag själv övergivet. Människan är extremt kontextbunden och överför färre av sina förmågor mellan sammanhang än vad hon tror. 

Kordasatsen är skitviktig om du ritat en cirkel med passare, tappat bort mittpunkten och behöver hitta den igen!

Hej! Vad är randvinkelsatsen? :O 

/ Mvh blivande naturare

soobin skrev:

Hej! Vad är randvinkelsatsen? :O 

/ Mvh blivande naturare

Läs här:

https://www.matteboken.se/lektioner/matte-2/geometri/randvinkelsatsen

Qetsiyah skrev:

Jag har hittills i universitetet inte behövt använda

• Sinussatsen
• Cosinussatsen
• Areasatsen
• Kordasatsen
• Randvinkelsatsen
• Bisektrissatsen
• Topptriangel/transversalsatsen

Så varför slösar man tid på det? Jag har faktiskt svårt att tänka mig scenarion/studieinriktningar där de skulle behövas (utom Lantmäteriprogrammet eller nåt).

Sen vet jag att det finns en egennytta med att studera matematik oberoende om stoffet är användbart eller inte, men helst borde man väl sikta på att göra bäggedera.

Håller helt klart med till viss del, trigonometrin skulle jag dock säga är väldigt användbar i vissa situationer, men geometriska bevis är väl kanske något man inte har speciellt mycket praktisk användning för, utan är mer som en introduktion till bevismetoder. 

Visste du att ett normerat linjärt rum, t ex ett Banachrum, kan göras Euklidiskt om det uppfyller parallellogramsatsen och blir då ett Hilbertrum (i Banachfallet)? Det säger mig att vi egentligen rotar i botten på grytan med de här satserna.

Tomten skrev:

Visste du att ett normerat linjärt rum, t ex ett Banachrum, kan göras Euklidiskt om det uppfyller parallellogramsatsen och blir då ett Hilbertrum (i Banachfallet)? Det säger mig att vi egentligen rotar i botten på grytan med de här satserna.

Vad betyder det? Är det du säger att "det är viktigt med geometrin på gymnasiet"?

ConnyN skrev:

Tomten skrev:

Visste du att ett normerat linjärt rum, t ex ett Banachrum, kan göras Euklidiskt om det uppfyller parallellogramsatsen och blir då ett Hilbertrum (i Banachfallet)? Det säger mig att vi egentligen rotar i botten på grytan med de här satserna.

Vad betyder det? Är det du säger att "det är viktigt med geometrin på gymnasiet"?

Det betyder att hen är en universitetsstudent som läste en kurs i funktionalanalys nyligen. Sedan kan Tomten såklart gärna dela ut insikterna hen fick där påverkat hur hen ser på hur viktigt det är med geometri i gymnasiet.

Hur är paralellogramvillkoret relevant här Tomten? Jag nämnde inte det och jag är ganska säker på att det inte kommer i gymnasiet.

Uppfattade din lista som exempel på Euklidiska satser vars vikt du ifrågasatte och menar med mitt exempel, att det inte går att klumpa ihop dessa och fälla någon dom. De spelar naturligtvis olika roll för olika personer och i olika sammanhang.