2
svar
84
visningar
heymel är nöjd med hjälpen
ordningen av ett gruppelement

alltså när de pratar om ordning, så säger def:
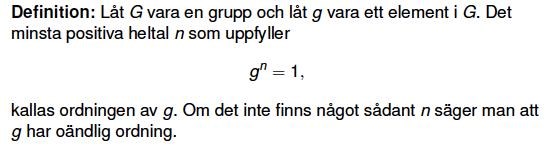
2^1 = 2 men inte = 1 men 2^4 = 16 = 1 .. hur har de "tänkt" där?
hmm.. ngn?
Gruppen kan betraktas som (utrustad med multiplikation av kongruensklasser som gruppoperation). Så när de skriver exempelvis "16", så menar de egentligen kongruensklassen .
Från tidigare i kursen kommer du säkert ihåg att , eftersom (detta föjer av att ).
På samma vis får vi att , eftersom (detta följer av att ).


