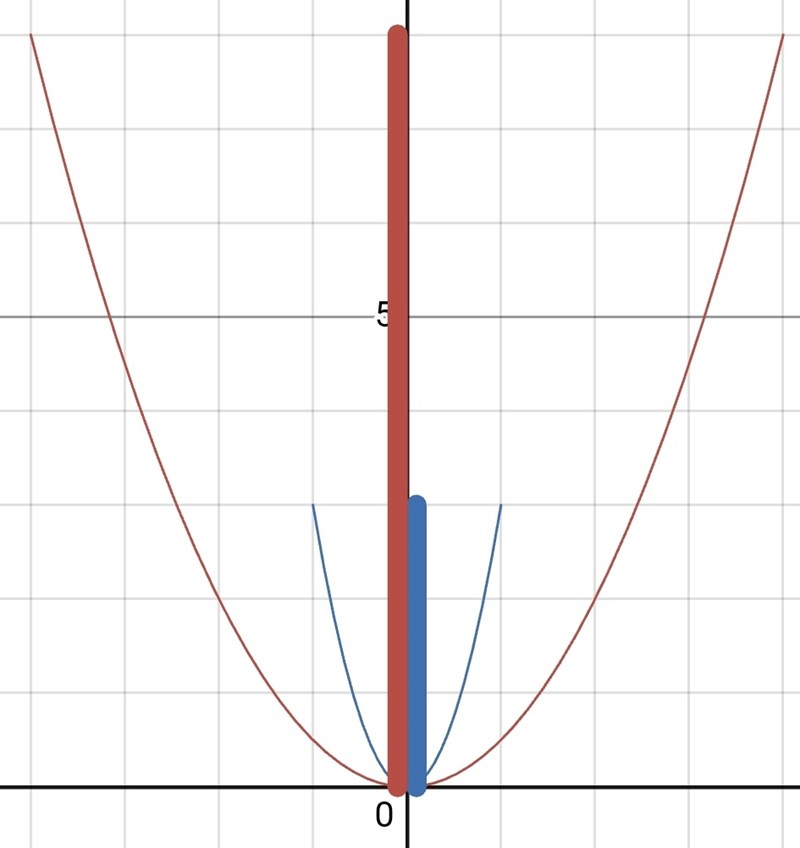
Parabler
Hej, har denna uppgift som jag är lite osäker på kring hur jag ska tänka kring.
uppgiften lyder:
A: y=0,5x2y=0,5x2 för (−4<x<4)
B: y=3x2y=3x2 för (−1<x<1)
vilken har störst värdemängd?
bara genom att se intervallet på A ser jag att det är större. Men jag tänkte att både har 0 som minsta värdemängd för att y inte kan anta ett negativt värde för det är en parabel. Men eftersom det står exempelvis x<4 att x är mindre än 4 är väl det största värdet på funktionen när x är 3 eller i alla fall 3,99 för det kan aldrig vara exakt 4. Ska jag skriva med 3.99 sådana fall och avrunda eller kör jag med 4 för i facit har de använt sig av x=4 och x=1 som högsta värdet.
Förlåt för den långa texten men det är sådant jag fastnar på och måste förstå för att gå vidare. All hjälp uppskattas!!
Hej.
Du tänker helt rätt och du kan bara svara att värdemängden är störst i A.
Men om du skulle vilja motivera ditt svar så kan du skriva att värdemängden i A är och att den i B är.
Att A har större definitionsmängd än B betyder dock inte att A har större värdemängd.
Yngve skrev:Hej.
Du tänker helt rätt och du kan bara svara att värdemängden är störst i A.
Men om du skulle vilja motivera ditt svar så kan du skriva att värdemängden i A är och att den i B är.
Yes så jag använder det största avrundade talet som 4 vilket ger 8 i värdemängden. För om jag hade typ 3.99 hade jag ändå kommit nära till 8. Så man ska tänka att talen vid olikhetstecken också är med i intervallet.
Med samma logik borde man kunna göra :
i uppgifter som y=8-x
-2<x≤4 och sedan har jag alternativ att välja mellan som skall ingå i intervallet.
för att fram det största värdemängden är det väl 8- (-2) =10 eftersom 10 var med som största alternativ.
Laguna skrev:Att A har större definitionsmängd än B betyder dock inte att A har större värdemängd.
Hur menar du
matte126 skrev:Laguna skrev:Att A har större definitionsmängd än B betyder dock inte att A har större värdemängd.
Hur menar du
Jag svarade på det här: "bara genom att se intervallet på A ser jag att det är större."
Vad menade du med det?
matte126 skrev:
Yes så jag använder det största avrundade talet som 4 vilket ger 8 i värdemängden. För om jag hade typ 3.99 hade jag ändå kommit nära till 8. Så man ska tänka att talen vid olikhetstecken också är med i intervallet.
Ja, så kan du tänka. Talen vid intervallets ändpunkter är "nästan" med i definitionsmängden, vilket innebär att motsvarande tal "nästan" är med i värdemängden.
Med samma logik borde man kunna göra :
i uppgifter som y=8-x
-2<x≤4 och sedan har jag alternativ att välja mellan som skall ingå i intervallet.
för att fram det största värdemängden är det väl 8- (-2) =10 eftersom 10 var med som största alternativ.
I det här fallet är det inte relevant att prata om "största" värdemängden eftersom det bara finns en sådan. Här är definitionsmängden och värdemängden blir då .
====
Det är ofta bra att använda något digitalt hjälpmedel för att rita graferna.
Yngve skrev:Hej.
Du tänker helt rätt och du kan bara svara att värdemängden är störst i A.
Men om du skulle vilja motivera ditt svar så kan du skriva att värdemängden i A är och att den i B är
Uppgiften är väldigt konstigt skriven och det skulle vara intressant att veta hur du tänkt när du skrev det här svaret. Hur kom du fram till y<8 och y<3?
Det är också tveksamt om vi kan bestämma att y>0. Vad jag kan se så är det inget som säger att den inte kan anta ett minusvärde. Det beror ju helt på vad parabeln illustrerar?
Detta är bara en undran från min sida.
Jag tror det är tänkt att uppgiften är något i stil med
Jag håller med om att uppgiften är underligt formulerad. Men jag är mer stressad över hur man vet vilken av de oändliga värdemängderna som är "störst". Antar dock att man ska mäta och jämföra intervallens längd på något sätt eller se det som en kuggfråga.
ConnyN skrev:
Uppgiften är väldigt konstigt skriven och det skulle vara intressant att veta hur du tänkt när du skrev det här svaret. Hur kom du fram till y<8 och y<3?
Jag "visste" hur de två graferna såg ut, att det i båda fallen var parabler med positiv koefficient framför x2-termen, dvs att båda parablerna såg ut som "glada munnar".
Då visste jag att y växer mer och mer ju längre bort man kommer från symmetrilinjen (som i båda fallen är x = 0). Då inser jag att y i A går mot 0,5*42 = 8 då x går mot 4 och mot 0,5*(-4)2 = 8 då x går mot -4.
På samma sätt inser jag att y i B går mot 3*12 = 3 då x går mot 1 och mot 3*(-1)2 = 3 då x går mot -1.
Det är också tveksamt om vi kan bestämma att y>0. Vad jag kan se så är det inget som säger att den inte kan anta ett minusvärde. Det beror ju helt på vad parabeln illustrerar?
Detta är bara en undran från min sida.
Nej, jag skrev att .
Att y inte kan vara < 0 i något av fallen inser man eftersom båda andrgradsuttryclen är av formen a*x2, där a > 0. Uttrycken saknar alltså både x-term och konstantterm.
======
Använd gärna något digitalt ritberktyg som.grafräknare, Desmos eller Geogebra för att rita graferna så ser du förhoppningsvis detta tydligt.
Yngve skrev:Använd gärna något digitalt ritberktyg som.grafräknare, Desmos eller Geogebra för att rita graferna så ser du förhoppningsvis detta tydligt.
Nja för den här uppgiften går det ganska bra med papper och penna.
Att tolka
A: y=0,5x2y=0,5x2 för (−4<x<4)
B: y=3x2y=3x2 för (−1<x<1)
är inte så lätt, men om det står A: med definitionsmängden
samt B: med definitionsmängden .
Då är min tolkning så här med papper och penna: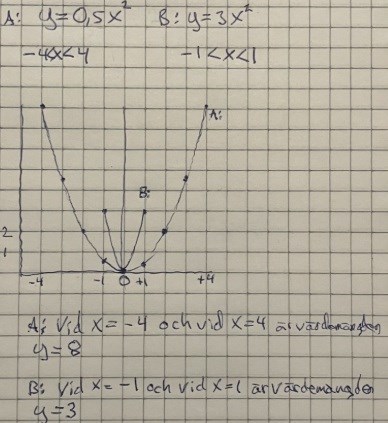
Ja, det är.så jag tolkar funktionerna.
Snygga grafer, men det du skriver på slutet stämmer inte. Dvs det är inte så att "Vid x = -4 och vid x = 4 är värdemängden y = 8". Värdemängden är en mängd, som i det här fallet innehåller (oändligt) många tal, varav 8 inte är ett.
Eftersom denna fråga är från Matte 1 så får vi säga att y närmar sig 8 mer och mer då x går mot 4 (eller mot -4). Men att y aldrig når värdet 8 eftersom x aldrig når värdet 4 (eller -4)
Om vi istället använder begreppet gränsvärde, som introduceras i senare mattekurser, så kan vi skriva .
Samma sak gäller för B, där är inte värdemängden 3.
Yngve skrev:Snygga grafer, men det du skriver på slutet stämmer inte. Dvs det är inte så att "Vid x = -4 och vid x = 4 är värdemängden y = 8". Värdemängden är en mängd, som i det här fallet innehåller (oändligt) många tal, varav 8 inte är ett.
Min tolkning är att texten "för (−4<x<4)" anger intervallet dvs. definitionsmängden, vilken beskrivs i matte 1.
I bokserien Matematik Origo matematik 1 finns denna beskrivning:
Definitionsmängden till en funktion är alla de värden som den oberoende variabeln kan anta.
Värdemängden till en funktion består av alla funktionsvärden som funktionen antar när den oberoende variabeln väljs ur definitionsmängden.
Om det är som jag tolkar det så kan inte värdemängden bestå av oändligt många tal. Om det nu är så att
(−4<x<4)" anger intervallet dvs. definitionsmängden för A: och (−1<x<1) för B:
Ja, du tolkar begreppen rätt. Men varför tycker du inte att värdemängderna kan bestå av oändligt många tal? Tänk på att de tal vi talar om (no pun intended) är både heltal, rationella tal (som t.ex. 5/9) och irrationella tal (som t.ex. ).
Yngve skrev:Ja, du tolkar begreppen rätt. Men varför tycker du inte att värdemängderna kan bestå av oändligt många tal? Tänk på att de tal vi talar om (no pun intended) är både heltal, rationella tal (som t.ex. 5/9) och irrationella tal (som t.ex. ).
Ja nu är jag med på vad du syftade på. Givetvis är det så. Jag är nog lite mer ringrostig än jag trodde 😊
Inget problem Conny, ringrost går.ju alltid att slipa bort.
Eftersom jag vet att du är intresserad av matematik så kan jag tipsa om ett vackert bevis av att antalet tal mellan t.ex. 0 och 1 inte bara är oändligt många, utan även att de är ouppräkneligt oändliga, dvs det går inte ens att räkna upp dem.
Vad gäller de rationella talen (som ju också är oändligt många) så är de uppräkneligt oändliga. Dvs det går (åtminstone i teorin) att göra en lista som innehåller alla rationella tal.
Men för irrationella tal så går det inte att göra en sådan lista.
Beviset är enkelt och elegant. Kika på Cantors diagonalbevis/diagonalargument
Det är enkelt att finna en bijektiv, strikt växande (ordningsbevarande) funktion mellan mängderna. Till exempel funktionen som givet ett element i mängden väljer korresponderande element i .
De två värdemängderna är därmed exakt lika stora (innehåller lika många korresponderande element). De har samma kardinalitet. Vilket alltså är det korrekta svaret på frågan.
Men förmodligen har konstruktören av frågan istället tänkt sig att man ska "mäta längden" av de halvöppna intervallen, vilket matematiskt sett är något helt annat.
Vi vet inte hur frågan var formulerad ursprungligen, men med tanke på att den kommer från Matte 1 så är det som avses säkerligen något i stil med "längden" på värdemängden som avses, dvs vilken av de vertikala staplarna som är längst.