Parametrisering i Linjeintegraler
Hej, jag har jättesvårt för att förstå parametrisering. En enkel regel jag lärt mig är att sätta x=t och därefter få allt annat beroende av t vilket fungerar ofta. Men en uppgift i Calculus får mig att höja ögonbrynen, jag förstår inte alls vad facit har gjort. 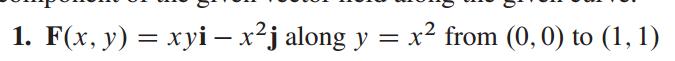
Här tänker jag att x = t, då blir y = t2. Av det blir då r(t) = (t3,-t2) (skriver vektor som (a,b,c) istället för i j k)
Här är fråga nummer 1 då, nu när uppgiften säger att man går från (0,0) till (1,1) är det ju ganska logiskt att parametriseringen går mellan 0<=t<=1. Men vad gör man om punkterna är (1,2) och (3,4)? Vad väljer man då för gränser?
Men vidare till facit som jag inte förstår då. 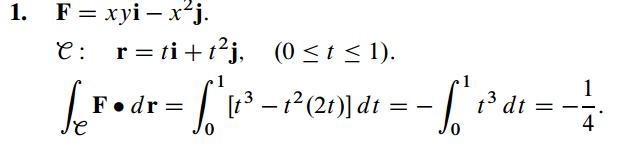
Här ser man att de har parametriserat r=(t,t^2) och det går bortom mitt förstånd hur de har gjort här. Gränserna är logiska. Formeln för en linjeintegral på ett begränsat område är
∫F·dr=∫baF(r(t))·drdtdt
och baserat på facit tror man ju då att de har satt x = t när de använder ekvationen, då de har [t3 (vilket bör motsvara x*y=t*t2 och -t2 . Men sen dyker (2t) upp från ingenstans. Om man nu ska multiplicera F där man byter ut x och y mot t/t2 och man sedan ska multiplicera med dr/dt borde dr/dt = 1 + 2t, inte som facit skrivit 2t? Dessutom bör väl det multipliceras med hela uttrycket f, inte bara -t2. Vad är det jag inte förstår?
F = (xy, -x2) = (t3, -t2).
r = (t, t2), dr = (1, 2t)dt
F∙dr = (t3, -t2)∙(1, 2t)dt = (t3 - 2t3)dt = -t3dt.
PATENTERAMERA skrev:F = (xy, -x2) = (t3, -t2).
r = (t, t2), dr = (1, 2t)dt
F∙dr = (t3, -t2)∙(1, 2t)dt = (t3 - 2t3)dt = -t3dt.
Gud vad jag är korkad, r är ju (x,y,z) fast med utbytta koordinater........


