Pascals formel
Någon som kan lösa denna?
Pascals formel säger att
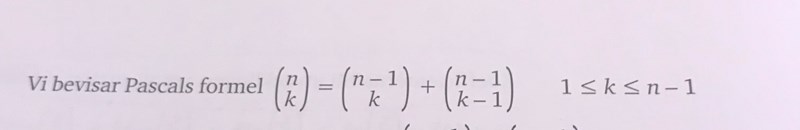
Men är det VL de vill att jag utvecklar? Förstår inte hur jag ska göra och finns ingen uppgift i boken som liknar denna..

Börja med att undersöka VL för några små värden på n, som 2, 3, 4... Ser du något mönster?
Du borde väl utveckla och skriva om till fakultet så du får bort "paranteserna"/matris.
Du har fått goda råd redan, men det lättaste sättet att lösa sådana här upogifter är med kombinatoriska resonemang
Vad gör jag för fel? Jag ser att det läggs till +1 i den övre men räknar jag fel på den nedre? Skulle vara enklare om jag kunde göra om till fakultet men förstår inte hur jag ska ställa upp det vänstra ledet i det..
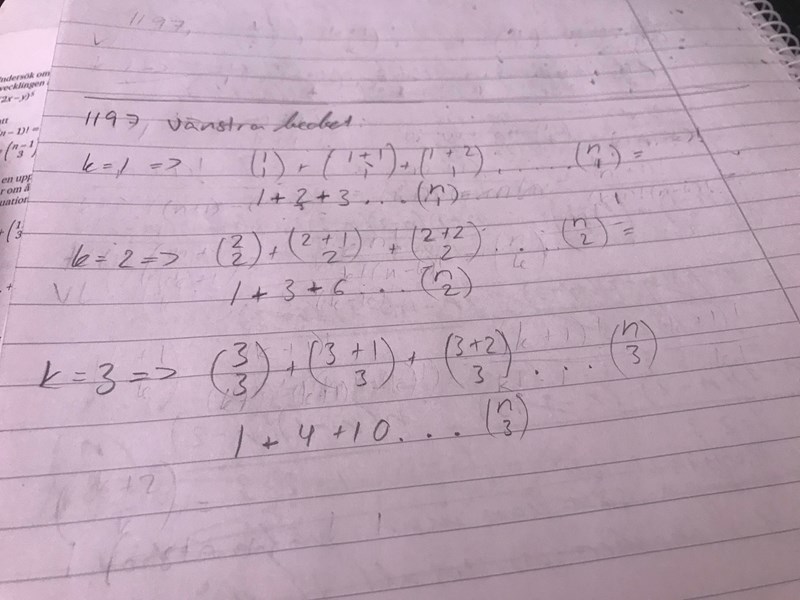
Om du byter ut k mot k+1 och n mot n+1 i den första formeln så får du nåt som du kan använda för att förenkla den andra formeln.
Jag ser inget direkt sätt att bevisa detta med fakultetsdefinitionen. Jag skulle nog göra ett induktionsbevis och ta hjälp av Pascals formel i induktionsbeviset.
Hej!
Pascals formel ger att så det gäller att visa att
Pascals formel ger igen att så det gäller att visa att
Fortsätt att arbeta dig ner i summan tills det enda som återstår är Pascals formel.





