påtvingad dämpad svängningsrörelse- resonans
En fjäderpendel har fjäderkonstanten 5,0 N/m, massan 0,10 kg och dämpningskoefficienten 0,080 kg/s. Den hålls igång med en kraft som varierar sinusformigt i tiden och har toppvärdet 0,10 N. Svängningens amplitud varierar me3d den drivande kraftens vinkelhastighet på det sätt som figuren visar.
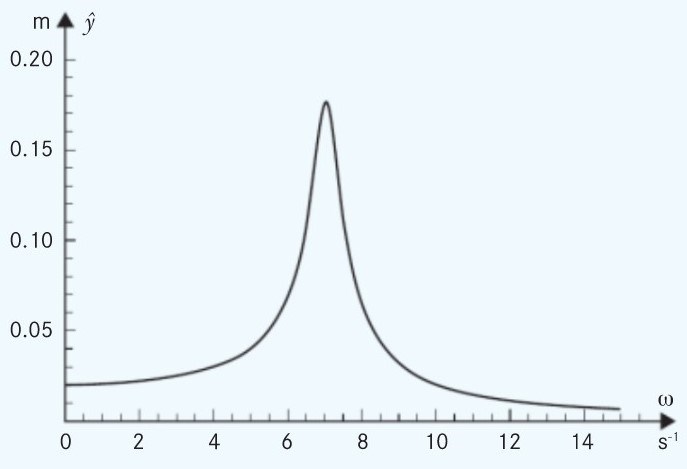
a) Teckna grafens ekvation.
b) Ange maximipunktens koordinater.
Resonansgrafens spetsighet kan anges med dess bredd, när genomsnittseffekten <P> är exakt hälften av genomsnittseffekten vid resonans.
c) Visa att detta inträffar när som innebär att .
a och b har jag löst korrekt. Men på del C har jag kört fast. Kan någon förklara vad de menar med den frågan?
Ska man förstå vad som menas med , och r? Och förmodligen refererar k till fjäderkonstanten men det framgår inte heller. Ytterst otydligt tycker jag, men det kanske är tydligare/uppenbart vad alla dessa betyder när man läser kursen? Tak, ^, brukar man kanske ha för att beteckna något tidsgenomsnitt och att då skulle vara något genomsnitt av den drivande kraften. Faktorn talar för att det kanske är något åt det hållet. Men varför använder de i så fall <P> och <PR> och inte resp ? Bortsett från alla otydligheter (för mig) så kan jag försöka ge lite tips så får vi se om du kan fortsätta själv.
De berättar att ett mått på spetsigheten av grafen är bredden när något effektvillkor är uppfyllt. Det kan man kanske förstå, att om man har en väldigt spetsig graf så är bredden vid det där okända stället mindre än om man har en vidare graf. Nu är det inte bredden som det frågas efter så det är bara en bakgrundsinformation för att öka förståelsen. Uppgiften går (i princip) ut på att bestämma för vilka som genomsnittseffekten är hälften av genomsnittseffekten vid resonans. Jag antar att genomsnittseffekt är definierad någonstans i boken annars är det troligt att man menar RMS-effekten (root mean square). Effekt är ju energi per tidsenhet (J/s) så den momentana effekten beskrivs av tidsderivatan av energin. Det betyder att om du kan sätta upp ett uttryck för den momentana energin så kan du beräkna genomsnittseffekten som funktion av . Då borde du vara nära en lösning.
Förmodligen finns det enklare lösningar som t.ex. kan utnyttja ekvationen från a).
Peter skrev:Ska man förstå vad som menas med , och r? Och förmodligen refererar k till fjäderkonstanten men det framgår inte heller. Ytterst otydligt tycker jag, men det kanske är tydligare/uppenbart vad alla dessa betyder när man läser kursen? Tak, ^, brukar man kanske ha för att beteckna något tidsgenomsnitt och att då skulle vara något genomsnitt av den drivande kraften. Faktorn talar för att det kanske är något åt det hållet. Men varför använder de i så fall <P> och <PR> och inte resp ? Bortsett från alla otydligheter (för mig) så kan jag försöka ge lite tips så får vi se om du kan fortsätta själv.
De berättar att ett mått på spetsigheten av grafen är bredden när något effektvillkor är uppfyllt. Det kan man kanske förstå, att om man har en väldigt spetsig graf så är bredden vid det där okända stället mindre än om man har en vidare graf. Nu är det inte bredden som det frågas efter så det är bara en bakgrundsinformation för att öka förståelsen. Uppgiften går (i princip) ut på att bestämma för vilka som genomsnittseffekten är hälften av genomsnittseffekten vid resonans. Jag antar att genomsnittseffekt är definierad någonstans i boken annars är det troligt att man menar RMS-effekten (root mean square). Effekt är ju energi per tidsenhet (J/s) så den momentana effekten beskrivs av tidsderivatan av energin. Det betyder att om du kan sätta upp ett uttryck för den momentana energin så kan du beräkna genomsnittseffekten som funktion av . Då borde du vara nära en lösning.
Förmodligen finns det enklare lösningar som t.ex. kan utnyttja ekvationen från a).
^-symbolen används för toppvärde i det läromedel som jag läser. Således är topphastigheten respektive kraftens maximivärde.
k är fjädernskonstant.
Grafens ekvation:
Den momentana effekten ges av kraften gånger hastigheten.
Du kan bilda <v>
Edit: uppgiftsskaparen ville visst att vi skulle gå över <v>
Jroth skrev:Den momentana effekten ges av kraften gånger hastigheten.
Du kan bilda <P>
det bör ge villkoret
Ska det inte stå sin i stället för cos i det första uttrycket? I så fall, blir då den genomsnittseffekten: , eller?
Undrar hur ska man få fram ett uttryck för genomsnittseffekten vid resonans?
Jroth skrev:Den momentana effekten ges av kraften gånger hastigheten.
Du kan bilda <v>
Edit: uppgiftsskaparen ville visst att vi skulle gå över <v>
Nu hänger jag inte med! Kan du förklara vad du menar?
Läser man uppgiftstexten verkar det som att uppgiftsskaparen vill att du ska utgå från följande
Sätter du in samt använder det uttryck du tog fram för den allmänna i uppgift a) ser du att uttrycket stämmer.
Beräknar du <P>= samt <P> = ser du att det blir halva beloppet.
Nu använder jag kanske inte exakt samma beteckningar som du gjort av den enkla anledningen att jag inte har sett vad du kallar dina parametrar men jag hoppas du kan förstå fysiken ändå.
.
Svag dämpning =>



