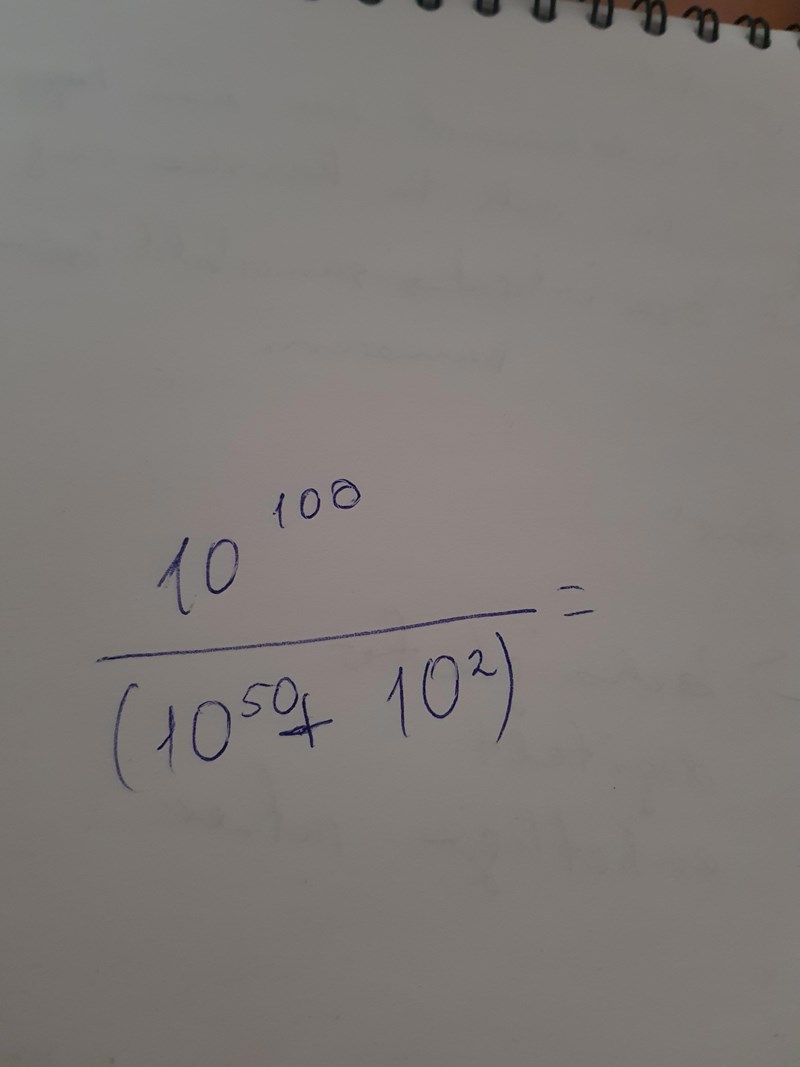Vad händer när du dividerar täljare och nämnare med ?
Hej
Kommer uppgiften ifrån en bok eller har du kommit på den själv?
Ser inget konkret förenkling utan av att bryta ut: , men det ger inget vidare. Har du testat och slagit det på t.ex. Wolframalpha?
Sedan kan man tillämpa att:
när (små värden på )
Affe Jkpg skrev:Sedan kan man tillämpa att:
när (små värden på )
Aha trevlig lösning. Tänkte mer på hur en åk 8 ska kunna lösa det ;).
jonis10 skrev:Hej
Kommer uppgiften ifrån en bok eller har du kommit på den själv?
Ser inget konkret förenkling utan av att bryta ut: , men det ger inget vidare. Har du testat och slagit det på t.ex. Wolframalpha?
Hej Jonis! Ja. Uppgiften är från boken Matte direkt 8. Tyvärr finns det inte fasit. Blir svaret då 10 upphöjd 50, om jag bortser +1
Affe Jkpg skrev:Sedan kan man tillämpa att:
när (små värden på )
Tack Affe, men det ser lite avancerad ut. Vi har inte lärt oss detta än :)
hjääälp skrev:Affe Jkpg skrev:Sedan kan man tillämpa att:
när (små värden på )
Tack Affe, men det ser lite avancerad ut. Vi har inte lärt oss detta än :)
Läste du min första ledtråd?
Affe Jkpg skrev:hjääälp skrev:Affe Jkpg skrev:Sedan kan man tillämpa att:
när (små värden på )
Tack Affe, men det ser lite avancerad ut. Vi har inte lärt oss detta än :)
Läste du min första ledtråd?
Affe Jkpg skrev:Affe Jkpg skrev:hjääälp skrev:Affe Jkpg skrev:Sedan kan man tillämpa att:
när (små värden på )
Tack Affe, men det ser lite avancerad ut. Vi har inte lärt oss detta än :)
Läste du min första ledtråd?
Tack snälla! Det här ser betydligt enklare ut!
Affe Jkpg skrev:Sedan kan man tillämpa att:
när (små värden på )
Jag lär mig (i princip) inte denna typ av approximationer utantill, för det finns ganska många men med små variationer. Jag lär mig i stället ett sätt att tänka, för att komma på aktuell formel. I detta fall börjar jag med att tänka:
Sedan kan man pröva något enkelt exempel på kalkylatorn. Som i detta fall:
Sedan är det inte så svårt att inse hur formeln för approximationen ska se ut.
Hej! Jag tänker så här:
är ett oerhört stort tal 10 000 000 ... ... ... Alltså 100 nollor efter 10.
är också ett stort tal, men ändå femtio nollor mindre.
är bara 100 och är försumbart litet i det här sammanhanget, så lösningen blir nästan exakt.
Jämför med astronomi där det kända universum är m då förstår man att 100 m är mycket mindre än en felmätning eller hur?