Potential

För ett konservativt fält gäller att gradienten av potentialen är lika med vektorfältet. Om du tar gradienten av U kommer du se att den skiljer sig från vektorfältet G. U är då inte en potential till fältet G.

G är alltså inte ett konservativt fält och saknar en potential.

Hur bestämde du potentialen U?

Jag adderar F med det som är givet och sen integrerar jag första delen av G med avseende på x och andra delen (efter kommatecknet) med avseende på y och sen får jag en potential av att "sätta ihop" de integrerade funktioner jag får. $\nabla U=(U_x\text{'}, U_y\text{'}) är vad jag lärt mig, och t.ex U_x\text{'} = x{y}^2 för F$

Nu spekulerar jag lite men vad du har hittat kanske är en potential för vissa värden. Potentialen ska ju fungera för alla kurvor där vektorfältet är definerad. Det kanske är så att potentialen du har bestämt stämmer för ett fåtal kurvor i R3. 

z-komponenten för fältet G och gradienten av U är samma.

x-komponenten är samma om xy - ysin(x) = 0.

y-komponenten är samma om $\frac{1}{2}{x}^2-x^{2}y-\frac{1}{2}xy-2\cos \left(x\right)-\cos \left(z\right)=0.$

Villkoren för x-komponenten och y-komponenten bildar tillsammans ett ekvationssystem som möjligtvis har en lösning. Då är det möjligt att potentialen stämmer för vissa kurvor i rummet. Och då har man väl på något sätt bestämt en potential till vektorfältet G, men det verkar ju konstigt att de efterfrågar en potential. Själv har jag i flervarren bara sett begreppet användas när man talar om konservativa fält.

Har du lyckats hitta något facit och sett hur de resonerar där?

Varför skulle det vara konstigt att de efterfrågar en potential till $G$? En potentialfunktion $U$ till ett vektorfält $G$ existerar om och endast om $G$ är konservativt. Så det innebär ju helt enkelt att $G$ är konservativt, om en potentialfunktion existerar.

Men när man räknar på fältet G får man att det inte är konservativt. 

Då saknar G en potential som är giltig över hela definitionsmängden.

Tyvärr inget facit är hittat, men Lasse har säkerligen rätt om att det troligtvis måste ha en potential över ett specifikt område i Df för att enligt definition om konservativa fält så är G inte konservativt för att Jakobimatrisen inte är symmetrisk. 

Jag känner inte till det där om jakobianen sedan tidigare. Skulle du kunna visa? Annars kan man kolla på fältets rotation eller curl som det heter och se om den är lika med noll.

Ett annat test man kan göra är att kolla om de olika partiella derivatorna i $\textbf{G}$ är lika med varandra. Exempelvis måste det gälla att:

$\displaystyle \frac{\partial (xy^2)}{\partial y}=\frac{\partial (x^2/2+\cos x)}{\partial x}$

Vilket inte stämmer. Så fältet kan inte vara konservativt och har därför ingen potentialfunktion. Spännande fråga...

(Det var säkert det du menade, Lasse)

Nu när jag kollar curl G får jag att curl G = (-sin(z))i + (x - 2xy - sin(x))k. Så curl G = 0 om -sin(z) = 0 och x - 2xy - sin(x) = 0. Då spottar wolfram ut följande lösning: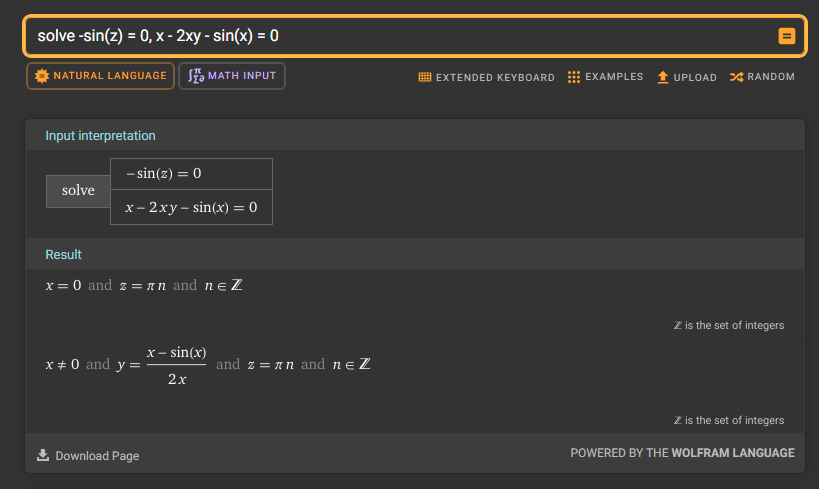

Du skulle kunna prova att beräkna en kurvintegral över någon kurva som utgörs av lösningen och se om du kan använda potentialen då.

naytte skrev:

Ett annat test man kan göra är att kolla om de olika partiella derivatorna i $\textbf{G}$ är lika med varandra. Exempelvis måste det gälla att:

$\displaystyle \frac{\partial (xy^2)}{\partial y}=\frac{\partial (x^2/2+\cos x)}{\partial x}$

Vilket inte stämmer. Så fältet kan inte vara konservativt och har därför ingen potentialfunktion. Spännande fråga...

---

(Det var säkert det du menade, Lasse)

Yes precis så.

Om Jakobianen av ett vektorfält är symmetrisk, betyder det att fältets komposanter uppfyller villkoren för att vara ett gradientfält, vilket innebär att fältet är konservativt + bevis om att området är enkelt sammanhängande. Min föreläsare tog upp detta, har fungerat bra för mig..

Jag undrar verkligen vad svaret är, men en generell fråga, vad borde hända om området inte är konservativt och jag försöker ta fram en potential. Hur kommer det se ut? Kommer jag nå något "olagligt" uttryck eller att t.ex 1=-1 som är olösbart? Hur kan jag känneteckna att potentialen inte finns?

Skulle tippa på att du helt enkelt får ett olösligt ekvationssystem. Men generellt gäller det att $\textbf{G}:=M\left(x,y,z\right)\hat{i}+N\left(x,y,z\right)\hat{j}+P\left(x,y,z\right)\hat{k}$ är ett konservativt vektorfält om och endast om:

$\displaystyle \frac{\partial M}{\partial y}=\frac{\partial N}{\partial x},\frac{\partial N}{\partial z}=\frac{\partial P}{\partial y},\frac{\partial M}{\partial z}=\frac{\partial P}{\partial x}$

Du behöver inte kolla mer än så. Här visar det sig redan i den första likheten att $\textbf{G}$ är icke-konservativt.

Vet inte riktigt. Jag tänker att det kan uttrycka sig i att du får olika svar när du löser kurvintegralen mha vanlig integrering vs användning av potentialer. Det var ett tag sedan jag bestämde potentialer så jag minns inte hur det bör se ut när man hittar en.

Den som kopierat uppgiften har skrivit fel. I originalet är F:s andra komponent 

x^2 + cos(z) 

Blir båda fälten konservativa då?

jamolettin skrev:

Den som kopierat uppgiften har skrivit fel. I originalet är F:s andra komponent 

x^2 + cos(z) 

 

Det du skickade med verkar inte komma upp, får jag fråga var du hittade uppgiften?

Uppgiften är från en gammal tenta på KTH. Det är möjligt att det är fler felskrivningar. 

Tanken är att F INTE är konservativ, men att G är konservativ. 

Felskrivning är rimligaste förklaringen. Är ju en tråkig uppgift om man kommer fram till att båda fälten inte är konservativa och slutar där haha.

jamolettin skrev:

Uppgiften är från en gammal tenta på KTH. Det är möjligt att det är fler felskrivningar. 

Tanken är att F INTE är konservativ, men att G är konservativ. 

Var kan jag komma åt den?

Om du känner någon som pluggar där så har väl de tillgång till gamla tentor? 

hur hittade du den? Har inte tillgång till detta..

Jag har konto och då hittade jag den. Vill dock inte publicera tentan här. 

Försökte skicka bild på uppgiften men det verkar inte funka.