Potentialfält
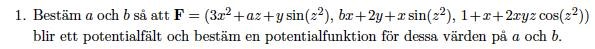
Om jag väljer att integrerar den första på x, sedan ska jag derivera den map y OCH z. Eller får man välja en utav dom ? Eller måste båda med?
Hej!
Du ska finna de tal och som gör att vektorfältets rotation försvinner,
Vet du hur man beräknar rotationen för ett vektorfält? (i rektangulära koordinater)
albibla skrev:Hej!
Du ska finna de tal och som gör att vektorfältets rotation försvinner,
Vet du hur man beräknar rotationen för ett vektorfält? (i rektangulära koordinater)
Yes.
Eftersom F=$(P,Q,R)$ är av klass $C^1$ i hela rummet så finns det en potentailfunktion omm rotF=0. Och eftersom vi har $(0,a-1,b)$ måste $a=1, b=0$.
Om $U$ är den potentialfunktionen vi söker så får vi med våra $a$ och $b$ att
Så integrarar map $x$ och får
Och så deriverar vi på $y$ ger Så Och
Men varför skall man derivera map z också?
mrlill_ludde skrev:albibla skrev:Hej!
Du ska finna de tal och som gör att vektorfältets rotation försvinner,
Vet du hur man beräknar rotationen för ett vektorfält? (i rektangulära koordinater)
Yes.
Eftersom F=$(P,Q,R)$ är av klass $C^1$ i hela rummet så finns det en potentailfunktion omm rotF=0. Och eftersom vi har $(0,a-1,b)$ måste $a=1, b=0$.Om $U$ är den potentialfunktionen vi söker så får vi med våra $a$ och $b$ att
Så integrarar map $x$ och får
Och så deriverar vi på $y$ ger Så Och
Men varför skall man derivera map z också?
För att bestämma den där psi(z).
Laguna skrev:mrlill_ludde skrev:albibla skrev:Hej!
Du ska finna de tal och som gör att vektorfältets rotation försvinner,
Vet du hur man beräknar rotationen för ett vektorfält? (i rektangulära koordinater)
Yes.
Eftersom F=$(P,Q,R)$ är av klass $C^1$ i hela rummet så finns det en potentailfunktion omm rotF=0. Och eftersom vi har $(0,a-1,b)$ måste $a=1, b=0$.Om $U$ är den potentialfunktionen vi söker så får vi med våra $a$ och $b$ att
Så integrarar map $x$ och får
Och så deriverar vi på $y$ ger Så Och
Men varför skall man derivera map z också?
För att bestämma den där psi(z).
Ahhh juste hehe
mrlill_ludde skrev:albibla skrev:Hej!
Du ska finna de tal och som gör att vektorfältets rotation försvinner,
Vet du hur man beräknar rotationen för ett vektorfält? (i rektangulära koordinater)
Yes.
Eftersom F=$(P,Q,R)$ är av klass $C^1$ i hela rummet så finns det en potentailfunktion omm rotF=0. Och eftersom vi har $(0,a-1,b)$ måste $a=1, b=0$.Om $U$ är den potentialfunktionen vi söker så får vi med våra $a$ och $b$ att
Så integrarar map $x$ och får
Och så deriverar vi på $y$ ger Så Och
Men varför skall man derivera map z också?
Det där är väl inte din egen text? Du har klippt och klistrat, eller hur?
Vad menar du till exempel med "Och eftersom vi har (0,a-1,b) måste a=1, b=0"?
För att förenkla beräkningarna av rotationen kan man dela upp vektorfältet i två komponenter där
och
Vektorfältets rotation blir en summa av två rotationer
där rotationen för det komplicerade vektorfältet visar sig vara noll.
Det gäller alltså att
och rotationen för det okomplicerade vektorfältet är lätt att beräkna.
albibla skrev:För att förenkla beräkningarna av rotationen kan man dela upp vektorfältet i två komponenter där
och
Vektorfältets rotation blir en summa av två rotationer
där rotationen för det komplicerade vektorfältet visar sig vara noll.
Det gäller alltså att
och rotationen för det okomplicerade vektorfältet är lätt att beräkna.
TacK =) ska kolla, på återseende :)


