Potentiell energi
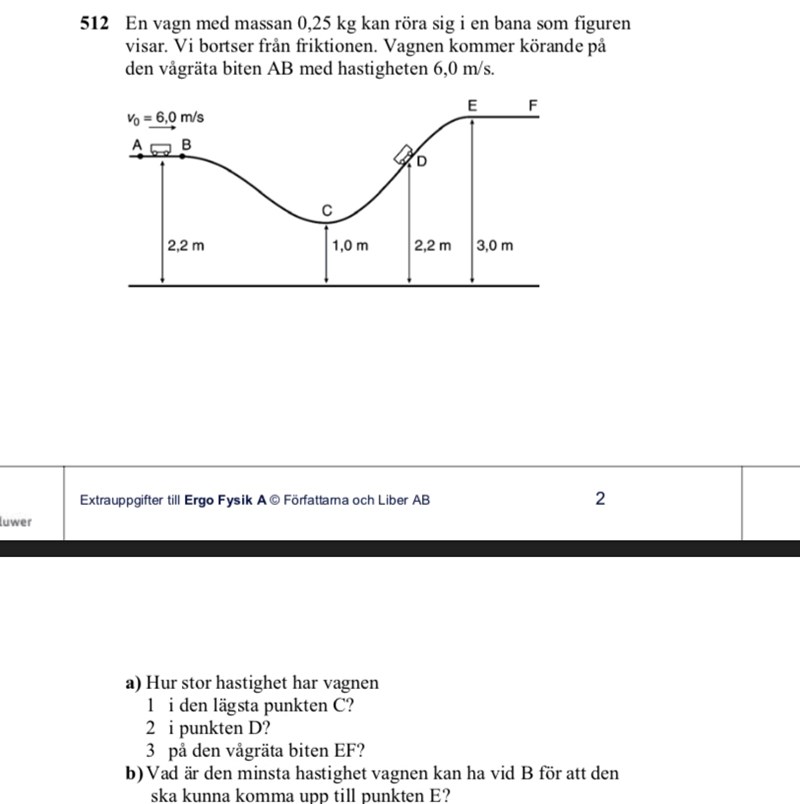
Hur löses denna uppgift? Jag försökte göra såhär:
mgh = mv^2/2
jag förkortade bort m och subratherade 2,2-1,0 för jag tror att man måste använda skillnaden i starthöjden och sluthöjden.
Jag får: 1,2 * 9,82 = V^2/2
2*11,784 = V^2
rotenur 23,568 = v
V = 4,9 m/s
försöker du göra 1) eller 2) ?
Qetsiyah skrev:försöker du göra 1) eller 2) ?
1!
Som du säger kan man förkorta bort m, men hur är det med starthastigheten? Den har du inte använt.
Laguna skrev:Som du säger kan man förkorta bort m, men hur är det med starthastigheten? Den har du inte använt.
Hur använder jag den? Kan du förklara hur jag löser den första uppgiften på rätt sätt.
Börja med att beräkna hur stor rörelseenergi och lägesenergi vagnen har i läge A.
Smaragdalena skrev:Börja med att beräkna hur stor rörelseenergi och lägesenergi vagnen har i läge A.
mgh = 2,2*9,82*0,25 = 5,401
mv^2/2 = 0,25^2/2 = 0,03125
Hur gör jag sedan?
I punkten C är summan av rörelseenergi och läges energi lika stor som vi punkten A.
Hur stor är lägesenergin? Hur stor är alltså rörelseenergin? Hur stor är hastigheten?
Smaragdalena skrev:I punkten C är summan av rörelseenergi och läges energi lika stor som vi punkten A.
Hur stor är lägesenergin? Hur stor är alltså rörelseenergin? Hur stor är hastigheten?
Hastigheten i A är ju 6,0 m/s. Jag tror att lägesenergin är 5,401 och rörelseenergin är 4,5. Detta fick jag åtminstone fram från min uträckning. Tänker jag rätt eller fel?
Vad har du använt för hastighet när du har beräknat rörelseenergin i punkten A?
EDIT: Såg att du har räknat om det, det hade du inte när jag började skriva.
Utgå från att summan av mekanisk energi är konstant, och fortsätt som jag beskriv i mitt förra inlägg.
Smaragdalena skrev:Vad har du använt för hastighet när du har beräknat rörelseenergin i punkten A?
EDIT: Såg att du har räknat om det, det hade du inte när jag började skriva.
Utgå från att summan av mekanisk energi är konstant, och fortsätt som jag beskriv i mitt förra inlägg.
Alltså ska jag ta den potentiella energin och addera med den kinetiska energin? Eller tänker jag helt fel nu?
Ja, du tänker helt fel. Du skall beräkna den potentiella energin i punkt C och subtrahera den från summan av potentiell och kinetisk energi i punkten A.
Smaragdalena skrev:Ja, du tänker helt fel. Du skall beräkna den potentiella energin i punkt C och subtrahera den från summan av potentiell och kinetisk energi i punkten A.
Jaha okej! Jag får svaret till 7,5 men i facit står det 7.7. Handlar det om avrundningsfel? För jag räknade ut den potentiella energin i C= mgh= 0,25*9,82*1,0= 2,455
5,401+4,5=9,901
9,901-2,455=7,446
Det ser ut som om du har beräknat rörelseenergin, men hur stor är hastigheten? Om du ser till att alltid ha koll på enheterna slipper du den sortens fel.
Smaragdalena skrev:Det ser ut som om du har beräknat rörelseenergin, men hur stor är hastigheten? Om du ser till att alltid ha koll på enheterna slipper du den sortens fel.
Oj jag vet inte. Tar jag min uträkning subtraherat med 6? Jag hänger inte riktigt med.
Hur beräknar du hastigheten, om du vet rörelseenergin? Tips: .
Smaragdalena skrev:Hur beräknar du hastigheten, om du vet rörelseenergin? Tips: .
Jag får ta rörelseenergin = mv^2/2 och lägga in siffrorna jag vet för att sedan lösa ut V. Är rörelseenergin 7,446 eller?
Student02 skrev:Smaragdalena skrev:Hur beräknar du hastigheten, om du vet rörelseenergin? Tips: .
Jag får ta rörelseenergin = mv^2/2 och lägga in siffrorna jag vet för att sedan lösa ut V. Är rörelseenergin 7,446 eller?
Behöver fortfarande hjälp med denna uppgift!
Vänta minst 24 timmar efter att trådens senaste inlägg publicerats innan du bumpar tråden. /Smutstvätt, moderator
Student02 skrev:Student02 skrev:Smaragdalena skrev:Hur beräknar du hastigheten, om du vet rörelseenergin? Tips: .
Jag får ta rörelseenergin = mv^2/2 och lägga in siffrorna jag vet för att sedan lösa ut V. Är rörelseenergin 7,446 eller?
Behöver fortfarande hjälp med denna uppgift!
Det är förståeligt. Läs vad t.ex. Smaragdalena skrev. Du verkar inte riktigt förstå vad du ska göra, och hens förslag om energiprincipen är korrekt. Du kan inte bara sitta och vänta på att någon ska lösa det åt dig. Försök sätta dig in i vad som sägs.
Eftersom detta är ett "standardproblem" så hjälper jag dig med att steg för steg lösa första uppgiften samtidigt som jag försöker förklara hur man kan tänka:
Hastigheten i punkt A (och B) är given, nämligen m/s. Det betyder att rörelseenergin i punkt A är J.
Höjden i punkt A är given, nämligen 2,2 m. Det betyder att lägesenergin i punkt A är J.
Den totala mekaniska energin i punkt A är alltså J.
När vagnen når punkt C (på höjd 1,0 m) så har den förlorat en del av sin lägesenergi eftersom lägesenergin nu endast är J.
Vagnen har samtidigt ökat hastigheten från 6,0 m/s till m/s och har då fått rörelseenergin J. Den totala mekaniska energin i punkt C är alltså J.
Eftersom vi försummar friktionen så omvandlas ingen energi till friktionsvärme. Detta betyder att den totala mekaniska energin i punkt A är lika stor som den totala mekaniska energin i punkt C.
OBS läs sista meningen igen och försök verkligen förstå, för det är denna princip som i stort sett alla liknande problem bygger på.
Det ger dig ekvationen .
Nu vill vi ta reda på vilket värde har, så vi löser ut ur ekvationen:
Börja med att dividera med på båda sidor:
Subtrahera g från båda sidor:
Multiplicera båda sidor med 2:
Dra roten ur båda sidor, den negativa roten är inte relevant:
Nu kan du stoppa in lämpligt närmevärde på g och beräkna hastigheten i C.
Hängde du med på hur man kan tänka och ställa upp det? Det handlar alltså om att införa okända storheter och ställa upp ekvationer utifrån principen att den totala mekaniska energin alltid är konstant (om man bortser från friktionen)
I så fall kan du använda samma typ av resonemang på övriga uppgifter.
(Och även på denna uppgift som du jobbade med tidigare.)
Yngve skrev:Eftersom detta är ett "standardproblem" så hjälper jag dig med att steg för steg lösa första uppgiften samtidigt som jag försöker förklara hur man kan tänka:
Hastigheten i punkt A (och B) är given, nämligen m/s. Det betyder att rörelseenergin i punkt A är J.
Höjden i punkt A är given, nämligen 2,2 m. Det betyder att lägesenergin i punkt A är J.
Den totala mekaniska energin i punkt A är alltså J.
När vagnen når punkt C (på höjd 1,0 m) så har den förlorat en del av sin lägesenergi eftersom lägesenergin nu endast är J.
Vagnen har samtidigt ökat hastigheten från 6,0 m/s till m/s och har då fått rörelseenergin J. Den totala mekaniska energin i punkt C är alltså J.
Eftersom vi försummar friktionen så omvandlas ingen energi till friktionsvärme. Detta betyder att den totala mekaniska energin i punkt A är lika stor som den totala mekaniska energin i punkt C.
OBS läs sista meningen igen och försök verkligen förstå, för det är denna princip som i stort sett alla liknande problem bygger på.
Det ger dig ekvationen .
Nu vill vi ta reda på vilket värde har, så vi löser ut ur ekvationen:
Börja med att dividera med på båda sidor:
Subtrahera g från båda sidor:
Multiplicera båda sidor med 2:
Dra roten ur båda sidor, den negativa roten är inte relevant:
Nu kan du stoppa in lämpligt närmevärde på g och beräkna hastigheten i C.
Hängde du med på hur man kan tänka och ställa upp det? Det handlar alltså om att införa okända storheter och ställa upp ekvationer utifrån principen att den totala mekaniska energin alltid är konstant (om man bortser från friktionen)
I så fall kan du använda samma typ av resonemang på övriga uppgifter.
Tack så mycket för detta! Jag ska verkligen analysera hur du löste denna uppgift så att jag kan lösa resterande själv!
Student02 skrev:
Tack så mycket för detta! Jag ska verkligen analysera hur du löste denna uppgift så att jag kan lösa resterande själv!
Bra. Gör det och ställ massor av frågor här kring det som du inte förstår. Då försöker vi förklara bättre.
När du sedan förstår principerna så kan du gå tillbaka och läsa t.ex. Smaragdalenas andra och tredje svar i denna tråd. Där står precis samma princip beskriven, fast med färre ord 😀.
Och efter det kan du gå tillbaka och titta på denna uppgift igen. Då blir den förhoppningsvis väldigt enkel att lösa.
Yngve skrev:Student02 skrev:Tack så mycket för detta! Jag ska verkligen analysera hur du löste denna uppgift så att jag kan lösa resterande själv!
Bra. Gör det och ställ massor av frågor här kring det som du inte förstår. Då försöker vi förklara bättre.
När du sedan förstår principerna så kan du gå tillbaka och läsa t.ex. Smaragdalenas andra och tredje svar i denna tråd. Där står precis samma princip beskriven, fast med färre ord 😀.
Och efter det kan du gå tillbaka och titta på denna uppgift igen. Då blir den förhoppningsvis väldigt enkel att lösa.
Tack så mycket! En grej nu när jag läser uppgiften noga är att du skrev ”subtrahera g från båda sidor” men du har ej subtraherat g på sidan där det står 18+2,2g? Istället står det 18+1,2g på nästa rad. Förstår inte riktigt. När jag löser ekvationen så får jag dock rätt svar! Är den mekaniska energin detsamma i D och EF?
Yngve skrev:Student02 skrev:Tack så mycket för detta! Jag ska verkligen analysera hur du löste denna uppgift så att jag kan lösa resterande själv!
Bra. Gör det och ställ massor av frågor här kring det som du inte förstår. Då försöker vi förklara bättre.
När du sedan förstår principerna så kan du gå tillbaka och läsa t.ex. Smaragdalenas andra och tredje svar i denna tråd. Där står precis samma princip beskriven, fast med färre ord 😀.
Och efter det kan du gå tillbaka och titta på denna uppgift igen. Då blir den förhoppningsvis väldigt enkel att lösa.

Nu när jag löser 2:an så får jag inte rätt svar :/
Student02 skrev:
Tack så mycket! En grej nu när jag läser uppgiften noga är att du skrev ”subtrahera g från båda sidor” men du har ej subtraherat g på sidan där det står 18+2,2g? Istället står det 18+1,2g på nästa rad. Förstår inte riktigt. När jag löser ekvationen så får jag dock rätt svar! Är den mekaniska energin detsamma i D och EF?
Om subtraktionen av : Jag hoppade över ett steg i uträkningarna. Om jag istället skriver ut alla steg blir det:
Subtrahera g från båda sidor:
Förenkla vänster- och högerled:
Och så vidare.
----
Om den mekaniska energin: Ja, den totala mekaniska energin (dvs summan av lägesenergi och rörelseenergi) är lika stor i alla punkter.
Student02 skrev:
Nu när jag löser 2:an så får jag inte rätt svar :/
Du ställer upp ekvationen rätt men sen blir det fel när du löser den.
Det är rätt fram till steget
Men sen blir det tokigt.
Subtrahera istället från båda sidor så får du
Förenkla och fortsätt.
Yngve skrev:Student02 skrev:
Nu när jag löser 2:an så får jag inte rätt svar :/
Du ställer upp ekvationen rätt men sen blir det fel när du löser den.
Det är rätt fram till steget
Men sen blir det tokigt.
Subtrahera istället från båda sidor så får du
Förenkla och fortsätt.
Jahaaa tack så himla mycket!
Yngve skrev:Student02 skrev:Tack så mycket! En grej nu när jag läser uppgiften noga är att du skrev ”subtrahera g från båda sidor” men du har ej subtraherat g på sidan där det står 18+2,2g? Istället står det 18+1,2g på nästa rad. Förstår inte riktigt. När jag löser ekvationen så får jag dock rätt svar! Är den mekaniska energin detsamma i D och EF?
Om subtraktionen av : Jag hoppade över ett steg i uträkningarna. Om jag istället skriver ut alla steg blir det:
Subtrahera g från båda sidor:
Förenkla vänster- och högerled:
Och så vidare.
----
Om den mekaniska energin: Ja, den totala mekaniska energin (dvs summan av lägesenergi och rörelseenergi) är lika stor i alla punkter.
Förstår inte riktigt uträkningen här. Du tar minus g på båda sidorna men låter forfarande g vara kvar i vänsterled? Hur får du 2,2g till 1,2g?
Student02 skrev:
Förstår inte riktigt uträkningen här. Du tar minus g på båda sidorna men låter forfarande g vara kvar i vänsterled? Hur får du 2,2g till 1,2g?
I vänsterled finns 2,2*g. Jag subtraherar g (dvs 1*g) därifrån och får då kvar 1,2*g:
Yngve skrev:Student02 skrev:Förstår inte riktigt uträkningen här. Du tar minus g på båda sidorna men låter forfarande g vara kvar i vänsterled? Hur får du 2,2g till 1,2g?
Jahaaa nu är jag med! Tack så mycket för all hjälp verkligen! En sista fråga, du sa innan att summan av Ep + Ek är lika stor i alla punkter, gäller dett alltid? Om jag hade fått en annan uppgift som liknande detta hade det gällt då? Eller beror det på typen av uppgift?
Student02 skrev:
Jahaaa nu är jag med! Tack så mycket för all hjälp verkligen! En sista fråga, du sa innan att summan av Ep + Ek är lika stor i alla punkter, gäller dett alltid? Om jag hade fått en annan uppgift som liknande detta hade det gällt då? Eller beror det på typen av uppgift?
Ja det gäller alltid under en viss förutsättning, nämligen att friktionen kan försummas, dvs att friktionen är väldigt väldigt liten i sammanhanget. Det betyder nämligen att ingen energi omvandlas till friktionsvärme under tiden och att alltså all förlust av lägesenergi blir till rörelseenergi och tvärtom.
I verkliga fall så kommer luftfriktion och rullfriktion att "stjäla" lite av den totala mekaniska energin när vagnen rullar. Den energi som på detta sätt "stjäls" från vagnen omvandlas till värme. Det är alltså fortfarande så att energin inte försvinner, den bara omvandlas till andra former.
Men håll utkik efter formuleringar som "rullar friktionsfritt", "friktionen kan försummas" eller som här "vi bortser från friktionen" i dina uppgifter. Om det står sådana saker så kan du räkna med att den totala mekaniska energin är lika stor i alla punkter.
Yngve skrev:Student02 skrev:Jahaaa nu är jag med! Tack så mycket för all hjälp verkligen! En sista fråga, du sa innan att summan av Ep + Ek är lika stor i alla punkter, gäller dett alltid? Om jag hade fått en annan uppgift som liknande detta hade det gällt då? Eller beror det på typen av uppgift?
Ja det gäller alltid under en viss förutsättning, nämligen att friktionen kan försummas, dvs att friktionen är väldigt väldigt liten i sammanhanget. Det betyder nämligen att ingen energi omvandlas till friktionsvärme under tiden och att alltså all förlust av lägesenergi blir till rörelseenergi och tvärtom.
I verkliga fall så kommer luftfriktion och rullfriktion att "stjäla" lite av den totala mekaniska energin när vagnen rullar. Den energi som på detta sätt "stjäls" från vagnen omvandlas till värme. Det är alltså fortfarande så att energin inte försvinner, den bara omvandlas till andra former.
Men håll utkik efter formuleringar som "rullar friktionsfritt", "friktionen kan försummas" eller som här "vi bortser från friktionen" i dina uppgifter. Om det står sådana saker så kan du räkna med att den totala mekaniska energin är lika stor i alla punkter.
Tack verkligen för all hjälp! På a) D nu när jag tittar i mitt häfte så har jag tydligen fått fel svar. Jag vet inte vad jag har gjort för fel, skulle du kunna hjälpa mig? 
Student02 skrev:
Tack verkligen för all hjälp! På a) D nu när jag tittar i mitt häfte så har jag tydligen fått fel svar. Jag vet inte vad jag har gjort för fel, skulle du kunna hjälpa mig?
Hej. Även nu ställer du upp ekvationen rätt men gör fel när du löser den.
Du förenklar högerledet och multiplicerar med 2 på en gång och då glömmer du att även multiplicera termen 0,8g med 2 (rödmarkerat i figuren här under).
Gör ett steg i taget så minskar risken för slarvfel.
Dvs förenkla först och multiplicera sedan.
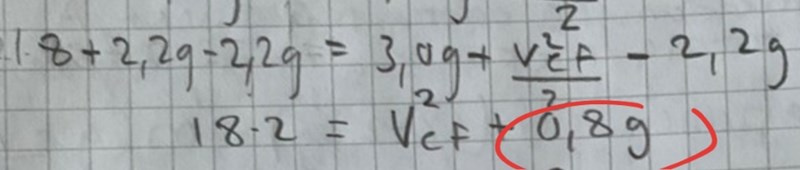
Yngve skrev:Student02 skrev:Tack verkligen för all hjälp! På a) D nu när jag tittar i mitt häfte så har jag tydligen fått fel svar. Jag vet inte vad jag har gjort för fel, skulle du kunna hjälpa mig?
Hej. Även nu ställer du upp ekvationen rätt men gör fel när du löser den.
Du förenklar högerledet och multiplicerar med 2 på en gång och då glömmer du att även multiplicera termen 0,8g med 2 (rödmarkerat i figuren här under).
Gör ett steg i taget så minskar risken för slarvfel.
Dvs förenkla först och multiplicera sedan.
Ahaa juste! Tack för att du tog din tid och förklarade allt detta för mig!
Hade jag kunnat få hjälp med B också? Hur går jag tillväga med den uppgiften. Är det samma princip eller?
Försök själv, så skall vi hjälpa dig om du kör fast.
Vilken rörelseenergi behöver vagnen ha vid E för att inte åka tillbaka?
Smaragdalena skrev:Försök själv, så skall vi hjälpa dig om du kör fast.
Vilken rörelseenergi behöver vagnen ha vid E för att inte åka tillbaka?
Den har ung 2,53 J. Detta fick jag åtminstone fram genom: mv^2/2 = 0,25*(4,5^2)/2 = 2,53
Nu är du fortfarande kvar på fråga a, verkar det som. Den hastigheten är inte aktuell längre. Nu frågar man vilken hastighet vagnen behöver ha vid B för att orka upp vid E.
Smaragdalena skrev:Nu är du fortfarande kvar på fråga a, verkar det som. Den hastigheten är inte aktuell längre. Nu frågar man vilken hastighet vagnen behöver ha vid B för att orka upp vid E.
Oj! Hur beräknar jag det? Förstår inte riktigt.
Student02 skrev:Smaragdalena skrev:Nu är du fortfarande kvar på fråga a, verkar det som. Den hastigheten är inte aktuell längre. Nu frågar man vilken hastighet vagnen behöver ha vid B för att orka upp vid E.
Oj! Hur beräknar jag det? Förstår inte riktigt.
Tänk så här: Vilken är den minsta hastigheten vagnen måste ha vid E för att nätt och jämnt nå dit?
Yngve skrev:Student02 skrev:Smaragdalena skrev:Nu är du fortfarande kvar på fråga a, verkar det som. Den hastigheten är inte aktuell längre. Nu frågar man vilken hastighet vagnen behöver ha vid B för att orka upp vid E.
Oj! Hur beräknar jag det? Förstår inte riktigt.
Tänk så här: Vilken är den minsta hastigheten vagnen måste ha vid E för att nätt och jämnt nå dit?
Är det 4,5 m/s? Alltså svaret på d i a) eller 6,0 m/s?
Student02 skrev:
Är det 4,5 m/s? Alltså svaret på d i a) eller 6,0 m/s?
Nej om den har hastigheten 4,5 m/s vid E så fortsätter den ju åt höger eftersom den har kvar rörelseenergi. Den hade i så fall kunnat ta sig upp för backen med lägre totalenergi att börja med.
Tänk istället att den bara har så mycket totalenergi att den nätt och jämnt orkar upp för backen. Vilken hastighet tror du då att den har vid E?
Yngve skrev:Student02 skrev:Är det 4,5 m/s? Alltså svaret på d i a) eller 6,0 m/s?
Nej om den har hastigheten 4,5 m/s vid E så fortsätter den ju åt höger eftersom den har kvar rörelseenergi. Den hade i så fall kunnat ta sig upp för backen med lägre totalenergi att börja med.
Tänk istället att den bara har så mycket totalenergi att den nätt och jämnt orkar upp för backen. Vilken hastighet tror du då att den har vid E?
Då måste det vara mindre än 4,5 m/s. Kanske 4,0 m/s?
Student02 skrev:Yngve skrev:Student02 skrev:Är det 4,5 m/s? Alltså svaret på d i a) eller 6,0 m/s?
Nej om den har hastigheten 4,5 m/s vid E så fortsätter den ju åt höger eftersom den har kvar rörelseenergi. Den hade i så fall kunnat ta sig upp för backen med lägre totalenergi att börja med.
Tänk istället att den bara har så mycket totalenergi att den nätt och jämnt orkar upp för backen. Vilken hastighet tror du då att den har vid E?
Då måste det vara mindre än 4,5 m/s. Kanske 4,0 m/s?
Ännu mindre. Om den har hastigheten 4,0 m/s så fortsätter den också till höger efter att den har kommit upp. Den har alltså en massa extra rörelseenergi över även efter att den klättrat uppför backen.
Vi prövar att istället tänka så här: Om vagnen nätt och jämnt tar sig upp för backen så kommer all dess rörelseenergi att gå åt till klättringen och helt och hållet gå över till lägesenergi. Den orkar alltså precis komma upp till E, sen orkar den inget mer.
Försök att se det framför dig. Vagnen rullar mödosamt uppför backen, långsammare och långsammare ...
Yngve skrev:Student02 skrev:Yngve skrev:Student02 skrev:Är det 4,5 m/s? Alltså svaret på d i a) eller 6,0 m/s?
Nej om den har hastigheten 4,5 m/s vid E så fortsätter den ju åt höger eftersom den har kvar rörelseenergi. Den hade i så fall kunnat ta sig upp för backen med lägre totalenergi att börja med.
Tänk istället att den bara har så mycket totalenergi att den nätt och jämnt orkar upp för backen. Vilken hastighet tror du då att den har vid E?
Då måste det vara mindre än 4,5 m/s. Kanske 4,0 m/s?
Ännu mindre. Om den har hastigheten 4,0 m/s så fortsätter den också till höger efter att den har kommit upp. Den har alltså en massa extra rörelseenergi över även efter att den klättrat uppför backen.
Vi prövar att istället tänka så här: Om vagnen nätt och jämnt tar sig upp för backen så kommer all dess rörelseenergi att gå åt till klättringen och helt och hållet gå över till lägesenergi. Den orkar alltså precis komma upp till E, sen orkar den inget mer.
Försök att se det framför dig. Vagnen rullar mödosamt uppför backen, långsammare och långsammare ...
Hmm... 2,0 m/s? Eller nu chansar jag bara! Finns det någon formel som vi måste utgå ifrån?
Student02 skrev:
Hmm... 2,0 m/s? Eller nu chansar jag bara! Finns det någon formel som vi måste utgå ifrån?
Ja nu chansar du bara.
Försök igen att se det hela framför dig. Låtsas nu att backen fortsätter uppåt efter punkten E.
Du står vid A och skjuter iväg vagnen med en viss hastighet.
Du ser att vagnen ökar hastigheten i nerförsbacken och att den sedan minskar hastigheten i uppförsbacken.
Den rullar långsammare och långsammare i uppförsbacken ju högre den kommer, eller hur?
Nu ser du att vagnen närmar sig punkten E. Spännande!
Du ser att vagnen precis når punkten E innan den vänder och rullar ner igen.
Ser du det hela framför dig?
Vilken hastighet har vagnen i punkten E, dvs precis när den vänder?
Yngve skrev:Student02 skrev:Hmm... 2,0 m/s? Eller nu chansar jag bara! Finns det någon formel som vi måste utgå ifrån?
Ja nu chansar du bara.
Försök igen att se det hela framför dig. Låtsas nu att backen fortsätter uppåt efter punkten E.
Du står vid A och skjuter iväg vagnen med en viss hastighet.
Du ser att vagnen ökar hastigheten i nerförsbacken och att den sedan minskar hastigheten i uppförsbacken.
Den rullar långsammare och långsammare i uppförsbacken ju högre den kommer, eller hur?
Nu ser du att vagnen närmar sig punkten E. Spännande!
Du ser att vagnen precis når punkten E innan den vänder och rullar ner igen.
Ser du det hela framför dig?
Vilken hastighet har vagnen i punkten E, dvs precis när den vänder?
Ja jag ser det hela framför mig! Hm... Tycker att det är så klurigt för vet inte riktigt hur jag ska sätta allt på plats. Vet inte riktigt vad den skulle kunna ha för hastighet innan den vänder men den måste väl vara hög, och sedan minskar den?
Student02 skrev:
Ja jag ser det hela framför mig! Hm... Tycker att det är så klurigt för vet inte riktigt hur jag ska sätta allt på plats. Vet inte riktigt vad den skulle kunna ha för hastighet innan den vänder men den måste väl vara hög, och sedan minskar den?
Ja hastigheten minskar på väg upp. Den minskar ner mot 0. Precis innan den vänder har den en väldigt väldigt låg hastighet, men den är fortfarande större än 0. Precis efter att den har vänt så har den också en väldigt väldigt låg hastighet, men denna hastighet är negativ, dvs mindre än 0.
Kan du då klura ut vilken hastighet vagnen har precis i vändpunkten, dvs i punkt E?
Tips: Så här ser v/t-diagrammet ut för vagnen i detta fallet då backen fortsätter uppåt:
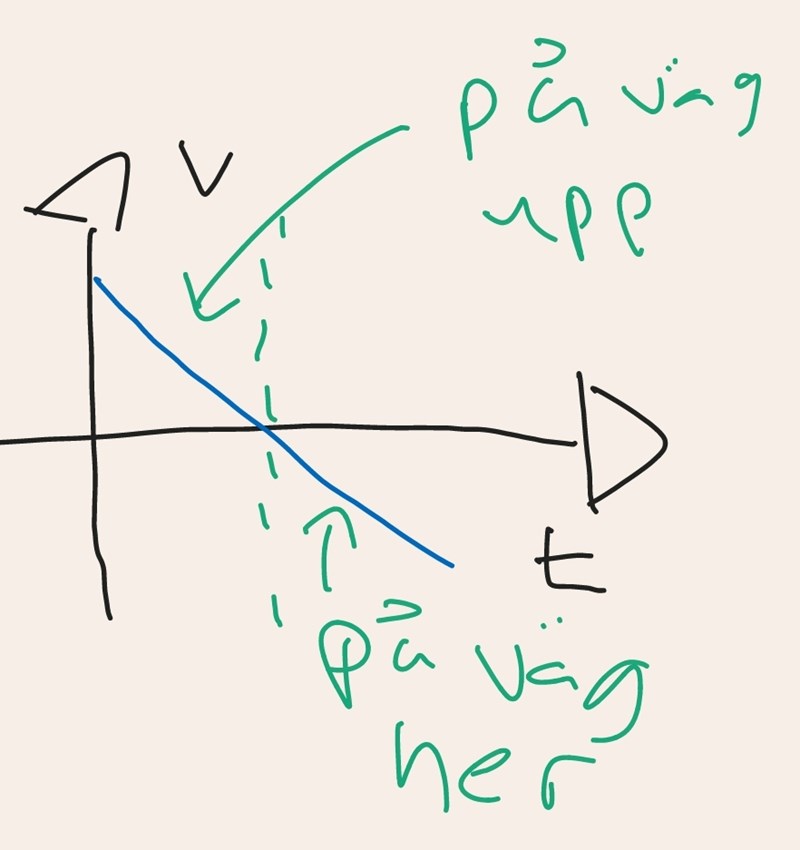
--------
Kommentar:
Det är precis samma sak som händer om du kastar en boll rakt upp i luften. På väg upp har bollen en hastighet, men den bromsas av gravitationen och stiger därför långsammare och långsammare. Vid en viss punkt så har bollen tappat hela sin hastighet och den vänder då neråt. Vad har bollen för hastighet i vändpunkten?
Om farten är för låg, kommer inte vagnen att orka uppför backen, utan den åker halvvägs upp, vänder och åker ner igen. Om farten är för hög, kommer vagnen att fortsätta åt höger. Vi söker den hastighet som gör att vagnen mätt och jämt orkar uppför backen, alltså kommer ända upp innan den vänder och åker ner igen.
Yngve skrev:Student02 skrev:Ja jag ser det hela framför mig! Hm... Tycker att det är så klurigt för vet inte riktigt hur jag ska sätta allt på plats. Vet inte riktigt vad den skulle kunna ha för hastighet innan den vänder men den måste väl vara hög, och sedan minskar den?
Ja hastigheten minskar på väg upp. Den minskar ner mot 0. Precis innan den vänder har den en väldigt väldigt låg hastighet, men den är fortfarande större än 0. Precis efter att den har vänt så har den också en väldigt väldigt låg hastighet, men denna hastighet är negativ, dvs mindre än 0.
Kan du då klura ut vilken hastighet vagnen har precis i vändpunkten, dvs i punkt E?
Tips: Så här ser v/t-diagrammet ut för vagnen i detta fallet då backen fortsätter uppåt:
--------
Kommentar:
Det är precis samma sak som händer om du kastar en boll rakt upp i luften. På väg upp har bollen en hastighet, men den bromsas av gravitationen och stiger därför långsammare och långsammare. Vid en viss punkt så har bollen tappat hela sin hastighet och den vänder då neråt. Vad har bollen för hastighet i vändpunkten?
Om hastigheten är - så tolkar jag det som att det måste vara minus den farten som det tar för vagnen att komma upp på E. Alltså -4,5? Känns helt fel men utifrån Vt-diagrammet så ser linjen ut att vara på samma siffror.
Smaragdalena skrev:Om farten är för låg, kommer inte vagnen att orka uppför backen, utan den åker halvvägs upp, vänder och åker ner igen. Om farten är för hög, kommer vagnen att fortsätta åt höger. Vi söker den hastighet som gör att vagnen mätt och jämt orkar uppför backen, alltså kommer ända upp innan den vänder och åker ner igen.
Ja men det känns som om det kan vara vad som helst. Är tanken att man chansar fram en fart? För jag tänkte först 4,0 sen 2,0 etc. Detta tänkte jag bara somsagt, räknade inte ut det genom någon formel vilket känns fel att inte göra.
Student02 skrev:
Ja men det känns som om det kan vara vad som helst. Är tanken att man chansar fram en fart? För jag tänkte först 4,0 sen 2,0 etc.
Vilken hastighet är det du gissar på?
Vi frågar efter hastigheten i punkt E, dvs i vändpunkten.
Sluta nu att gissa och svara istället på följande frågor:
- Om hastigheten i punkt E är större än 0 så kommer vagnen att fortsätta uppför backen, är du med på det?
- Då skulle inte vändpunkten vara vid punkten E utan den skulle då vara högre upp i backen, är du med på det?
Yngve skrev:Student02 skrev:Ja men det känns som om det kan vara vad som helst. Är tanken att man chansar fram en fart? För jag tänkte först 4,0 sen 2,0 etc.
Vilken hastighet är det du gissar på?
Vi frågar efter hastigheten i punkt E, dvs i vändpunkten.
Sluta nu att gissa och svara istället på följande frågor:
- Om hastigheten i punkt E är större än 0 så kommer vagnen att fortsätta uppför backen, är du med på det?
- Då skulle inte vändpunkten vara vid punkten E utan den skulle då vara högre upp i backen, är du med på det?
Jag är med på båda frågor, precis som du beskrev i ett föregående svar så åker ju vagnen upp men sedan ner igen.
Student02 skrev:Yngve skrev:
Vilken hastighet är det du gissar på?
Vi frågar efter hastigheten i punkt E, dvs i vändpunkten.
Sluta nu att gissa och svara istället på följande frågor:
- Om hastigheten i punkt E är större än 0 så kommer vagnen att fortsätta uppför backen, är du med på det?
- Då skulle inte vändpunkten vara vid punkten E utan den skulle då vara högre upp i backen, är du med på det?
Jag är med på båda frågor, precis som du beskrev i ett föregående svar så åker ju vagnen upp men sedan ner igen.
Bra. Och då kommer fråga 3:
3. Vilken hastighet har vagnen i vändpunkten E, dvs där den vänder och åker ner igen?
Yngve skrev:Student02 skrev:Yngve skrev:Vilken hastighet är det du gissar på?
Vi frågar efter hastigheten i punkt E, dvs i vändpunkten.
Sluta nu att gissa och svara istället på följande frågor:
- Om hastigheten i punkt E är större än 0 så kommer vagnen att fortsätta uppför backen, är du med på det?
- Då skulle inte vändpunkten vara vid punkten E utan den skulle då vara högre upp i backen, är du med på det?
Jag är med på båda frågor, precis som du beskrev i ett föregående svar så åker ju vagnen upp men sedan ner igen.
Bra. Och då kommer fråga 3:
3. Vilken hastighet har vagnen i vändpunkten E, dvs där den vänder och åker ner igen?
4,0 m/s? Jag tänker det eftersom på fråga a) så var svaret 4,5 m/s och då så känns det som om att - 0,5 m/s hade varit perfekt för att detta ska kunna ske. Om svaret ska vara minus så borde det i sådana fall vara -4,0.
Ta ett papper och knöla ihop det till en boll. Kasta den rakt uppåt, men inte så hårt att den slår i taket. Observera hur pappersbollen bromsar in, vänder och börjar falla neråt igen, med ökande hastighet. Vilken hastighet har pappersbollen precis i vändläget?
Smaragdalena skrev:Ta ett papper och knöla ihop det till en boll. Kasta den rakt uppåt, men inte så hårt att den slår i taket. Observera hur pappersbollen bromsar in, vänder och börjar falla neråt igen, med ökande hastighet. Vilken hastighet har pappersbollen precis i vändläget?
0? Tycker detta är så svårt :/
Student02 skrev:
4,0 m/s? Jag tänker det eftersom på fråga a) så var svaret 4,5 m/s och då så känns det som om att - 0,5 m/s hade varit perfekt för att detta ska kunna ske. Om svaret ska vara minus så borde det i sådana fall vara -4,0.
Menar du alltså att vagnen har hastigheten 4,0 m/s i punkt E?
Du har ju själv nyss skrivit att du förstod att vagnen i så fall skulle fortsätta upp för backen och att vändpunkten då onte alls ligher i E utan högre ipp i backen?
Alltså kan vagnen inte ha en hastighet större än 0 vid punkt E.
Strunta i vad svaret på fråga a var nu.
Glöm vagnen för en stund så prövar vi något annat.
---------
Titta istället på bollen du kastar rakt upp i luften.
Vi undrar vilken hastighet bollen har i det ögonblick då den når vändpunkten, dvs vid sin högsta punkt.
Om det är svårt att komma fram till det så kan du tänka så här. På väg upp genpm luften så minskar bollens rörelseenergi samtidigt som dess lägesenergi ökar.
När den når vändpunkten har all dess rörelseenergi övergått till lägesenergi .
Den har då ingen rörelseenergi kvar alls, dvs . Eftersom så måste det betyda att hastigheten är lika med ... ja vad då tror du?
-------
EDIT - ser nu att du redan kommit fram till rätt svar på hastigheten vid vändläget.
Yngve skrev:Student02 skrev:
4,0 m/s? Jag tänker det eftersom på fråga a) så var svaret 4,5 m/s och då så känns det som om att - 0,5 m/s hade varit perfekt för att detta ska kunna ske. Om svaret ska vara minus så borde det i sådana fall vara -4,0.
Menar du alltså att vagnen har hastigheten 4,0 m/s i punkt E?
Du har ju själv nyss skrivit att du förstod att vagnen i så fall skulle fortsätta upp för backen och att vändpunkten då onte alls ligher i E utan högre ipp i backen?
Alltså kan vagnen inte ha en hastighet större än 0 vid punkt E.
Strunta i vad svaret på fråga a var nu.
Glöm vagnen för en stund så prövar vi något annat.
---------
Titta istället på bollen du kastar rakt upp i luften.
Vi undrar vilken hastighet bollen har i det ögonblick då den når vändpunkten, dvs vid sin högsta punkt.
Om det är svårt att komma fram till det så kan du tänka så här. På väg upp genpm luften så minskar bollens rörelseenergi samtidigt som dess lägesenergi ökar.
När den når vändpunkten har all dess rörelseenergi övergått till lägesenergi .
Den har då ingen rörelseenergi kvar alls, dvs . Eftersom så måste det betyda att hastigheten är lika med ... ja vad då tror du?
-------
EDIT - ser nu att du redan kommit fram till rätt svar på hastigheten vid vändläget.
Åh okej så svaret är 0 bara? Tack så mycket för denna förklaring!
Svaret på vilken hastighet vagnen skall ha i vändläget E är 0, men det man frågar efter är vilken hastighet vagnen skall ha i läge B för att ha hastigheten 0 i vändläget E. Har du någon aning om hur du skall komma fram till detta?
Student02 skrev:Åh okej så svaret är 0 bara? Tack så mycket för denna förklaring!
Nej svaret är inte 0.
Du vill att hastigheten vid punkten E ska vara 0 m/s, för då når vagnen nätt och jämnt upp dit.
Allt detta resonemang om vändpunkter, positiva och negativa hastigheter, bollar som kastas hit och dit var alltså bara för att komma fram till vilken hastighet som vagnen ska ha vid punkt E så att den nätt och jämnt orkar upp dit.
Nu kan du starta om och lösa uppgiften.
Du har alltså att
- Höjden vid punkt B är 2,2 m.
- Hastigheten vid punkt B är v m/s. Det är den du ska ta reda på.
- Höjden vid punkten E är 3,0 m.
- Hastigheten vid punkten E är 0 m/s.
Använd nu samma typ av resonemang som du gjorde på de tidigare uppgifterna, dvs summan av den mekaniska energin är lila stor vid B som vid E.
Och ta reda på vad v då blir.
Klarade du av uppgiften efter vår hjälp?
Yngve skrev:Klarade du av uppgiften efter vår hjälp?
Hej! Hann inte titta på det igår eftersom jag var tvungen att sova inför skolan och har ej hunnit idag pga skola. Ska titta på det såfort jag kommer hem och återkommer om jag har frågor! Tack så hemskt mycket för all den hjälpen jag har fått dock.






