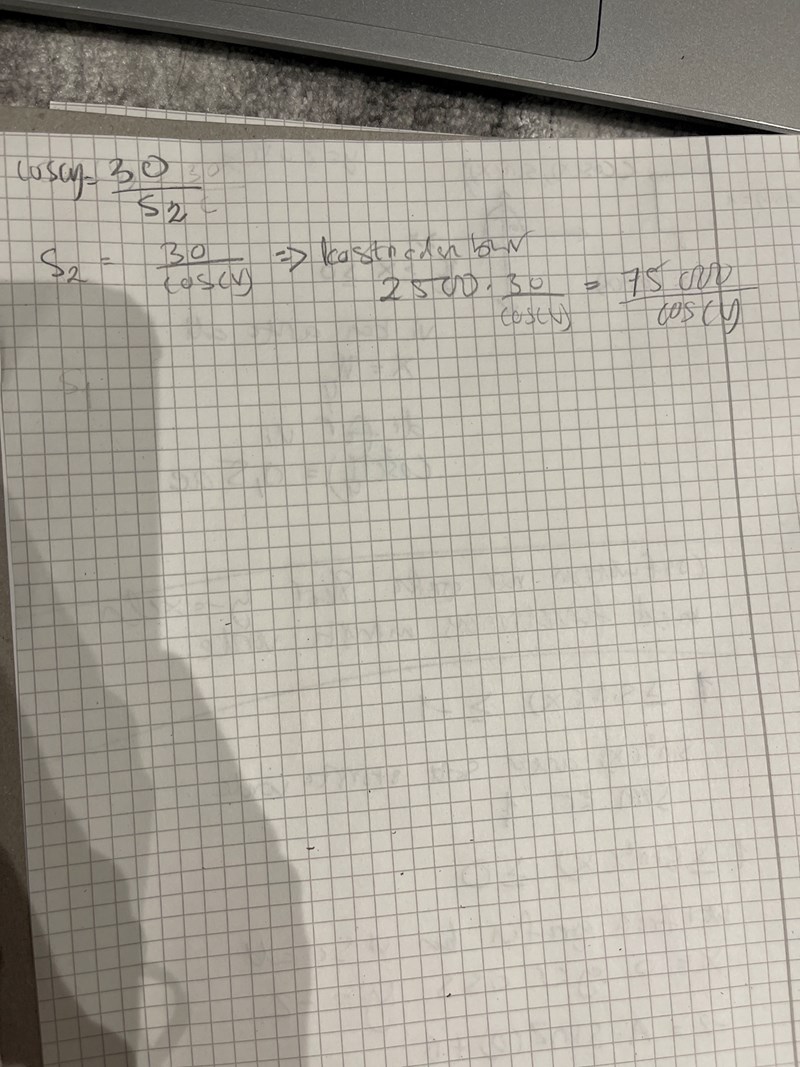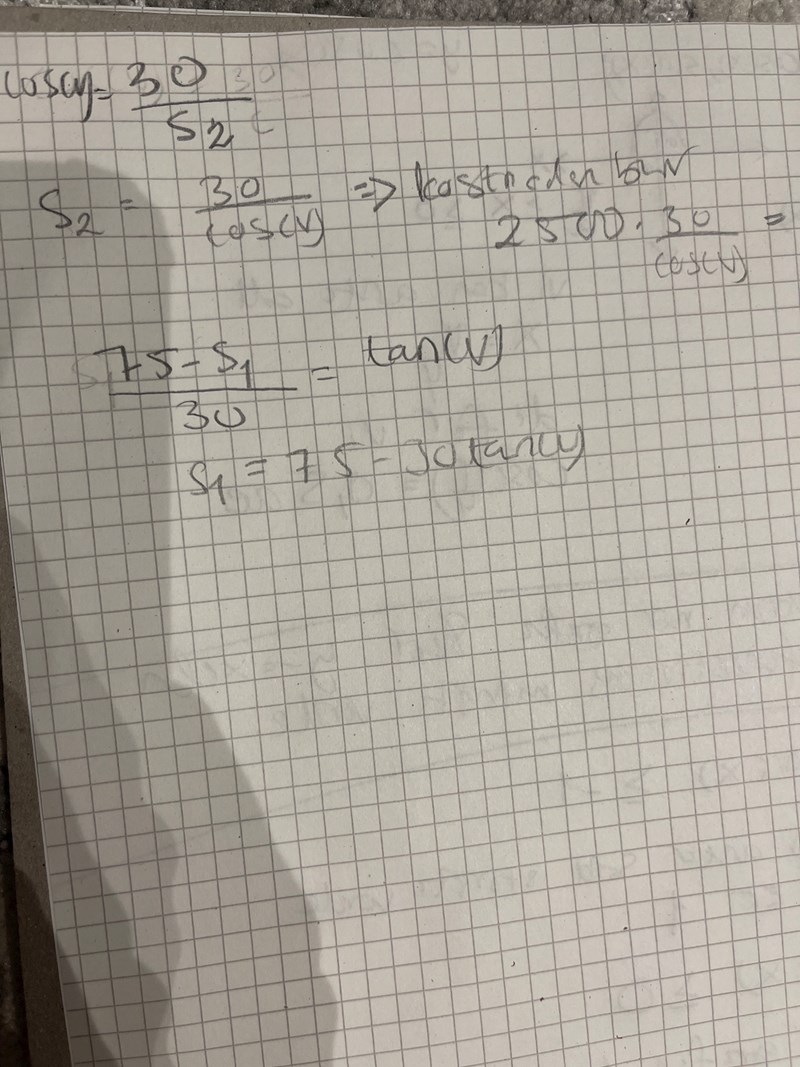Problemlösning trigonometri (bestäm vinkeln v)
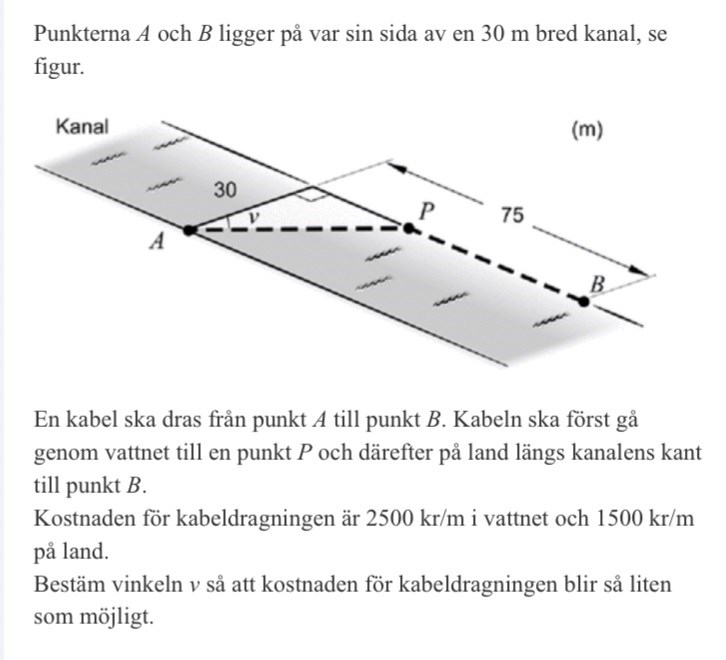En av de svåraste uppgifterna jag stött på hittills. Jag vet inte ens vart jag ska börja eller vad det är jag ska göra…? Hur ska man tänka?
Oftast när det gäller att hitta minsta "någonting" eller största "någonting" så gäller det att
- sätta upp ett funktionsuttryck som ska minimeras eller maximera
- derivera detta uttryck
- sätta derivatan lika med 0
- lösa den ekvationen
Derivatans nollställen ger oss då funktionens stationära punkter och vi kan då ta reda på om dessa punkter är min-, max- eller terrasspunkter på lite olika sätt.
I det här fallet ska du alltså försöka sätta upp ett uttryck för kostnaden K som beror av vinkeln v, dvs du ska bestämma K(v). Sedan kan du derivera till K'(v) och så vidare.
Börja med att bestämma uttryck för de båda sträckorna som beror av vinkeln v.
Förstår du då vad du ska göra?
Det enda jag har lyckats skriva upp är att cos(v)=30/C
Vad är C?
C är hypotenusan i triangeln
Ja, bra, då har du att C, dvs sträckan AP, är lika med 30/cos(v).
Försök nu att hitta ett uttryck för sträckan PB
Jag antar att S1 är sträckan PB och att S2 är sträckan AP.
Då stämmer dina uttryck.
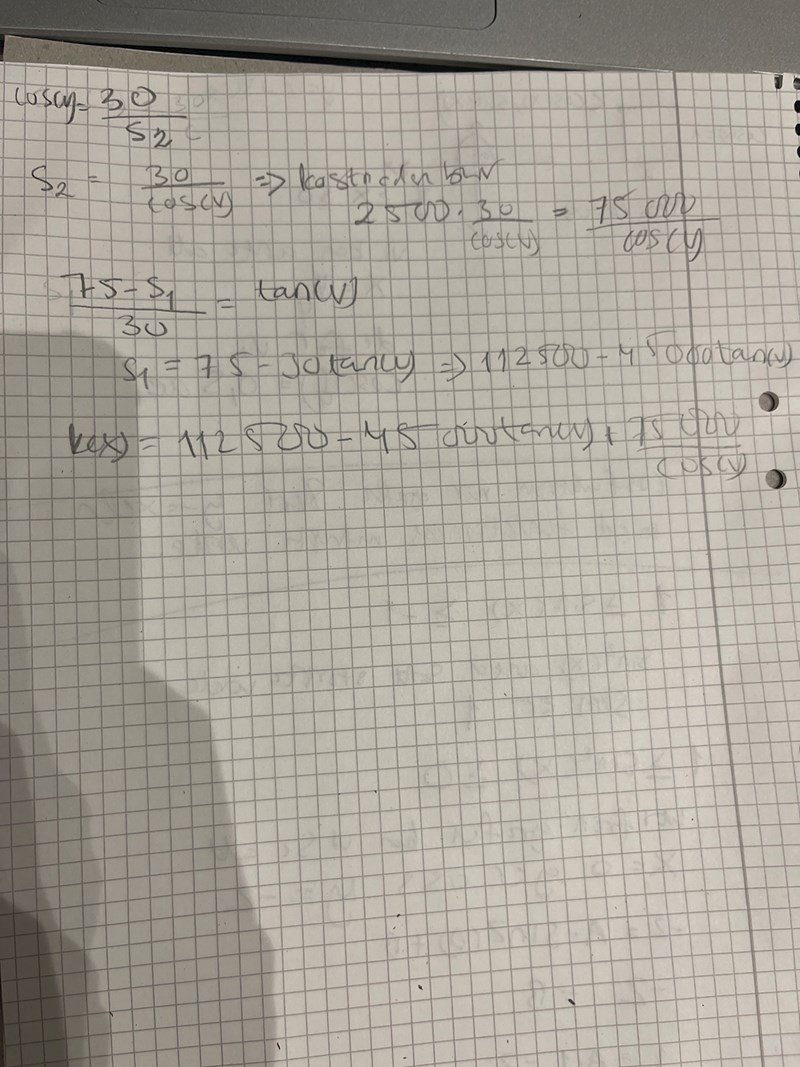Ska jag lösa det algebraiskt eller grafiskt?
Pröva algebraiskt. Kontrollera din lösning med hjälp av grafräknaren.
Vad är det jag ska göra? Derivera sen sätta y värdet till noll?
Ja, som jag skrev i det här svaret.
Hur deriverar man tan(v)?och 75 000/tan(v)?
Titta i din formelsamlung eller skriv tan(x) som sin(x)/cos(x) och använd formeln för derivatan av en kvot
Menar du kvotregeln
