Produktregel bevis.

Hej

Tänkte på ett bevis av produktregeln med hjälp av derivatans definition, det verkar som att man bestämmer sig för att addera f(x) g(x+h)- f(x) g(x+h) för att göra beviset möjligt. Varför gör man så? Om man måste "lägga till" någonting till derivatans definition..då känns det lite som att det egentligen inte gäller, typ. Isf kan man ju lägga till och klippa och klistra som man vill så man får det resultat man är ute efter, så länge man håller sig inom reglerna dvs..

Fast kanske är så det går till.

Du adderar egentligen ingenting. Det som sker är att du adderar något, och direkt subtraherar det.

Man kan lägga till 2-2 till ett uttryck. Eftersom 2-2=0 ändras inget. I vissa fall kan ett visst uttryck hjälpa till för att komma fram i mål och då kan man helt enkelt introducera uttrycket genom att addera och subtrahera det!

Jo.

Men det går alltså inte att komma fram till rätt svar utan att genomföra det här momentet?

Ja, om det ska härledas via definitionen.

Det är det klassiska sättet att göra det på. Jag kan inte komma på något annat snyggt sätt att göra det på med derivatans definition.

Leibniz tänkte i termer av infinitesimaler och tänkte ungefär så här:

$\displaystyle \mathrm{d}(xy)=(x+\mathrm{d}x)(y+\mathrm{d}y)-xy=x\mathrm{d}y+y\mathrm{d}x+\mathrm{d}x\mathrm{d}y$

Sedan insåg han att $\mathrm{d}x\mathrm{d}y$ är oändligt mycket mindre än resten av termerna, och således försumbar*:

$\displaystyle \mathrm{d}(xy)=x\mathrm{d}y+y\mathrm{d}x$

vilket är den klassiska produktreglen skriven på differentialform. Låt säga att både $x$ och $y$ är beroende av en oberoende variabel $t$ . Om vi delar med $\mathrm{d}t$ har vi:

$\displaystyle \frac{\mathrm{d}(xy)}{\mathrm{d}t}=x\frac{\mathrm{d}y}{\mathrm{d}t}+y\frac{\mathrm{d}x}{\mathrm{d}t}$

vilket är produktregeln så som vi är vana vid att se den.

*Det här med att produkten av två differentialer är försumbar är lite besvärligt. Det är naturligtvis lite nonsensaktigt att påstå att man bara kan "ta bort" en term. Faktum är att Leibniz arbetade med en utvidgad likhetsrelation, så han påstod aldrig att det var ett direkt likhetstecken, utan i hans värld var det något utvidgat likhetstecken. Men jag är inte så väl inläst på exakt hur han tänkte kring den biten, jag vet bara att folk hatar för mycket på honom för detta.

Men liksom om du sitter med det här för första gången och ska bevisa regeln utan att det har gjorts tidigare, då kommer man bara på då att ja, men jag adderar och subtraherar det här så får jag regeln att stämma?

Så först räknar man derivatan manuellt av ex (x^2)(x^3), och ser då att det inte är så enkelt som att bara multiplicera dem, sedan leker man med definitionen ända tills man ser att det fungerar?

Dkcre skrev:
Men liksom om du sitter med det här för första gången och ska bevisa regeln utan att det har gjorts tidigare, då kommer man bara på då att ja, men jag adderar och subtraherar det här så får jag regeln att stämma?

Så först räknar man derivatan manuellt av ex (x^2)(x^3), och ser då att det inte är så enkelt som att bara multiplicera dem, sedan leker man med definitionen ända tills man ser att det fungerar?

Det kan vara ganska svårt att hitta sådana här knep för att lösa uppgifter. Jag, som älskar integraler, ser liknande saker ganska ofta. Att addera och subtrahera samma sak kan vara otroligt användbart (kan återkomma med ett exempel när min huvudvärk gått över).

Oftast kan motivationen vara att man ser någon förenkling ifall man hade ett visst uttryck. Då kan man helt enkelt introducera det genom att bara addera och subtrahera det.

Jag tror att vi har diskuterat denna fråga tidigare, men det kokar tyvärr ned till "man måste bara se det". Den här typen av mekanisk matematik har mycket med igenkänning att göra; ju fler situationer man har varit i, desto bättre blir ens igenkänningsförmåga.

Det är lite som schack, om du har spelat det. Visserligen kan talang och andra medfödda förutsättningar göra det lättare, men i grunden måste alla nöta. Det finns inga knep eller genvägar. Nöta, nöta, nöta!

Jo. När man blir tillräckligt duktig och erfaren inom någonting så kan man använda sig av det på ett annat sätt. Ganska tillfredsställande.

Men tänker att om det inte fanns någon särskild regel och man själv skulle få lov att hitta på den, då vet man ju inte nödvändigtvis hur produktregeln ser ut. Man vet inte hur slutresultatet ska se ut eller vad som fungerar. Tänker att man först mekaniskt måste räkna ut det och sedan hitta ett mönster därefter. Fast ganska självklart kanske, svårt att komma med en lösning på ett problem som inte existerar ^^

Jo. Har spelat schack, ganska roligt men har ingen fallenhet för det. Det fastnar inte riktigt. Men känner till att det är viktigt med igenkänning där, exempelvis det som ska ha särskilt utmärkt Kasparov ska ha varit hans exceptionella minne och alla mönster han kunde. Sen är väl mannen naturligtvis halvt begåvad i övrigt också men.

AlexMu skrev:
Kan återkomma med ett exempel när min huvudvärk gått över

Okej, jag kommer med två exempel här. Mitt första exempel är inte något som egentligen visar hur användbart det är, kanske bara ett lite trevligt fall just här. Dock är det andra exemplet lite över matte 4 nivå och kan vara lite svårare att hänga med på. Däremot tycker jag det tydligt visar användbarheten!

Exempel 1

Visa spoiler

Om man vill ta derivatan av

\frac{x}{1+x}

är min första tanke hur mycket jag ogillar att använda kvot/produktregeln. I detta fall behöver man faktiskt inte göra det! Om man adderar och subtraherar

1

får man lite trevlig förenkling:

\displaystyle \frac{x}{1+x} = \frac{x + {\color{blue} 1-1}}{1+x}=\frac{x+{\color{blue}1}}{x+1}-\frac{{\color{blue}1}}{1+x} = 1- \frac{1}{1+x}

Nu kan vi ta derivatan genom att bara använda kedjeregeln!

Som jag sa, detta exempel är inte super-representativt. Detta gör algebran lite lättare om man ser detta, men man kan fortfarande lösa problemet med en annan regel (och att tänka ut detta tar nog, för många, längre tid än att använda de andra deriveringsreglerna).

Exempel 2

Visa spoiler

En ganska intressant integral är

$\displaystyle I = \int\limits_0^{\pi/2}{\frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}}\mathrm dx}$

Nu kan man tänka sig: Om vi hade en $\sqrt{\cos x}$ -term i täljaren så skulle allt ta ut varandra och vi skulle få kvar $1$ . Så vi testar att introducera denna term:

$\displaystyle I = \int\limits_0^{\pi/2}{\frac{\sqrt{\sin x}+{\color{blue}\sqrt{\cos x}-\sqrt{\cos x}}}{\sqrt{\sin x}+\sqrt{\cos x}}\mathrm dx}=\int\limits_0^{\pi/2}{\left(\frac{\sqrt{\sin x}+{\color{blue}\sqrt{\cos x}}}{\sqrt{\sin x}+\sqrt{\cos x}}-\frac{\color{blue}\sqrt{\cos x}}{\sqrt{\sin x}+\sqrt{\cos x}}\right)\mathrm dx}$
$\displaystyle = \int\limits_0^{\pi/2}{\left(1-\frac{\sqrt{\cos x}}{\sqrt{\sin x}+\sqrt{\cos x}}\right)\mathrm dx}$

Nu kan vi dela upp denna i två integraler:

$\displaystyle I = \int\limits_0^{\pi/2}1\mathrm dx-\int\limits_0^{\pi/2}{\frac{\sqrt{\cos x}}{\sqrt{\sin x}+\sqrt{\cos x}}\mathrm dx}$

Den första integralen kan vi beräkna genom att hitta antiderivatan, eller att bara uppfatta den som arean under $y=1$ från $0$ till $\pi/2$ , vilket då är $\pi/2$ .

$\displaystyle I = \frac{\pi}2-\int\limits_0^{\pi/2}{\frac{\sqrt{\cos x}}{\sqrt{\sin x}+\sqrt{\cos x}}\mathrm dx}$

Slutligen kan man visa (ingår ej i ma4, men man kan tänka sig fram till varför det måste stämma utan integrationsteknikerna som annars används för att visa det) att

$\displaystyle \int\limits_0^{\pi/2}{\frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}}\mathrm dx} = \int\limits_0^{\pi/2}{\frac{\sqrt{\cos x}}{\sqrt{\cos x}+\sqrt{\cos x}}\mathrm dx}$

Det kanske blir tydligt om man kollar på en graf av funktionerna: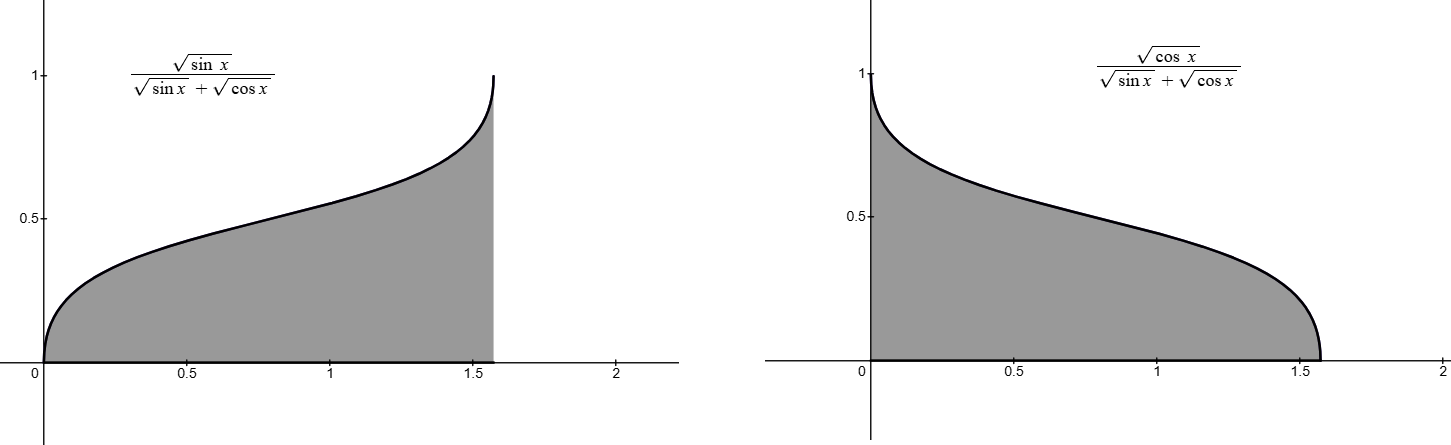
Eftersom vi hade från början att

$\displaystyle I =\int\limits_0^{\pi/2}{\frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}}\mathrm dx}$ får vi automatiskt att

$\displaystyle I = \int\limits_0^{\pi/2}{\frac{\sqrt{\cos x}}{\sqrt{\sin x}+\sqrt{\cos x}}\mathrm dx}$ också!

Men om vi kollar igen på det vi kom fram till tidigare,

$\displaystyle I = \frac{\pi}2-\underbrace{\int\limits_0^{\pi/2}{\frac{\sqrt{\cos x}}{\sqrt{\sin x}+\sqrt{\cos x}}\mathrm dx}}_{I}$

Så har vi att integralen i HL är $I$ . Alltså gäller det att

$\displaystyle I = \frac{\pi}2 - I$

Så $\displaystyle 2I = \frac{\pi}2$

Vilket ger oss

$\displaystyle I = \frac{\pi}{4}$

Alltså är

$\displaystyle \int\limits_0^{\pi/2}{\frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}}\mathrm dx} = \frac{\pi}4$

Vilket vi kom fram till med detta "knep" UTAN att ens beräkna antiderivatan (det kommer inte gå särskilt bra om man försöker det).

Mathematica ger att antiderivatan är:

Inte särskilt trevligt (och förmodligen inte särskilt hjälpsamt eftersom EllipticPi är en speciell funktion som definieras av en integral ändå (kan fortfarande vara hjälpsamt, men det är definitivt svårare att hitta denna antiderivata än att lösa integralen som vi gjorde)).

Tack för exemplen. Integralen kan jag inte avläsa alls än men förstår den första 😊

Svara

Visa senaste svar