Punkt P roteras 90° moturs runt punkten Q
Uppgiften lyder:
Det finns två punkter, punkten P =(c, d) och punkten Q =(a, b). Punkten P roteras 90° moturs runt punkten Q, vilka koordinater har punkten P efter rotationen?
Jag fick fram svaret P=(-c, d) såhär:
k1* k2 = -1
k1=
då måste ju k2 =
då drar jag slutsatsen att de nya koordinaterna för P är (d, -c)
min fråga är nu om detta resonemanget stämmer eller om jag har tänkt fel någonstans.
Tack!
Nej, tänk t.ex att (a,b) = (0,0) och (c,d) = (1,0). (c,d) skulle då roteras till (0,1), men din formel säger (-1,0).
Har du ritat?
Pröva!
Låt P vara origo och Q vara punkten (1, 0).
Fungerar din teori då?
Dr. G skrev:Nej, tänk t.ex att (a,b) = (0,0) och (c,d) = (1,0). (c,d) skulle då roteras till (0,1), men din formel säger (-1,0).
Har du ritat?
Nej, försökte lösa det rent logiskt, men insåg nu att det inte stämmer. Ska prova att rita.
Dr. G skrev:Nej, tänk t.ex att (a,b) = (0,0) och (c,d) = (1,0). (c,d) skulle då roteras till (0,1), men din formel säger (-1,0).
Har du ritat?
Efter lite eftertanke och en graf har jag kommit fram till att om (a, b) = (0, 0), och (c, d) = (1, 0), så skulle den nya punkten kunna beskrivas med (a, c). Stämmer detta eller är det också fel?
Nja.
Men det är en bra idé att börja med att Q är origo.
Låt P ligga någonstans i första kvadranten. Då bör punkten efter rotation hamna i andra kvadranten, eller hur? Och var?
Dr. G skrev:Nja.
Men det är en bra idé att börja med att Q är origo.
Låt P ligga någonstans i första kvadranten. Då bör punkten efter rotation hamna i andra kvadranten, eller hur? Och var?
Om vi säger att punkt P ligger i första kvadranten med koordinaterna (1, 0), då blir väl de nya koordinaterna efter en rotation på 90° (0, 1)? (0, 1) ligger väl inte i andra kvadranten?
Oklart om en punkt på positiv y-axel ligger i någon kvadrant, eller mellan två kvadranter. Antingen så ligger den mellan första och andra kvadranterna, eller så ligger den i både första och andra kvadranterna. Jag vet inte vilken definition som är den vanliga.
Dr. G skrev:Nja.
Men det är en bra idé att börja med att Q är origo.
Låt P ligga någonstans i första kvadranten. Då bör punkten efter rotation hamna i andra kvadranten, eller hur? Och var?
Jag har tänkt en stund nu och har verkligen ingen aning. Jag kan få fram k-värdet på linjen som skär Q och P, samt Q och P efter vridningen, men hur jag ska komma fram till vilken punkt P får efter rotationen vet jag inte.
Det ser ut ungefär så här.
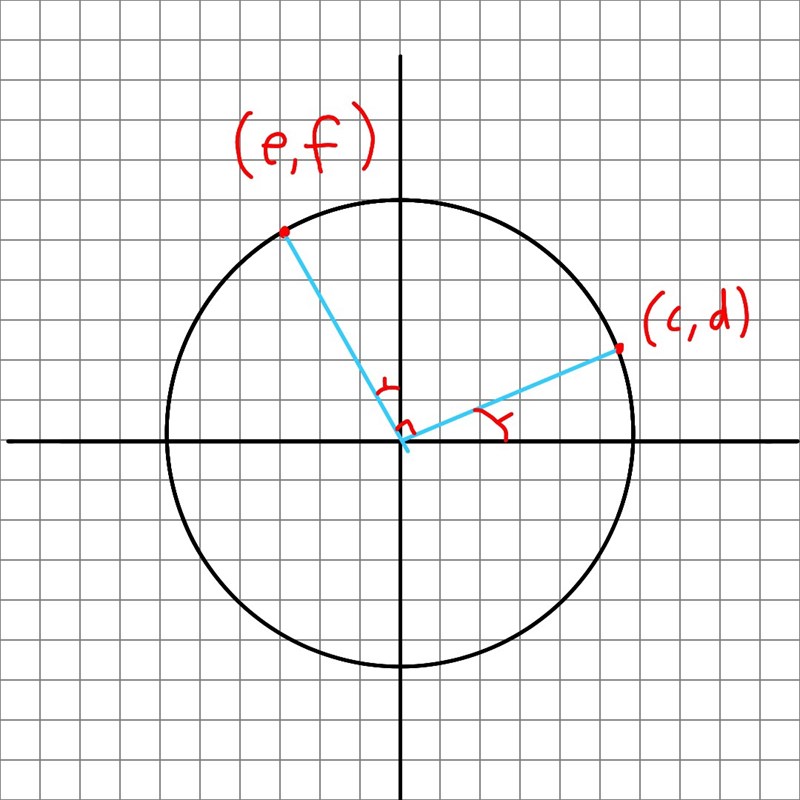
Du vet koordinaterna (c,d) och vill hitta koordinaterna efter rotation (e,f). Se om du hittar två likformiga (t.o.m kongruenta) trianglar i figuren.




