Punkten (3.y) ligger lika långt från origo som från punkten (2,4). Bestäm y.
Ser ut som att du har ställt upp det lite konstigt. Testa att sätta upp ett uttryck för avståndet mellan origo och (2,4), och ett uttryck mellan origo och (3,y). Sätt sen dessa uttryck lika med varandra
Toffelfabriken skrev:Ser ut som att du har ställt upp det lite konstigt. Testa att sätta upp ett uttryck för avståndet mellan origo och (2,4), och ett uttryck mellan origo och (3,y). Sätt sen dessa uttryck lika med varandra
Inte riktigt. Testa att rita upp det och se hur du kan få ut avståndet mellan origo och (2,4).
Toffelfabriken skrev:Ser ut som att du har ställt upp det lite konstigt. Testa att sätta upp ett uttryck för avståndet mellan origo och (2,4), och ett uttryck mellan origo och (3,y). Sätt sen dessa uttryck lika med varandra
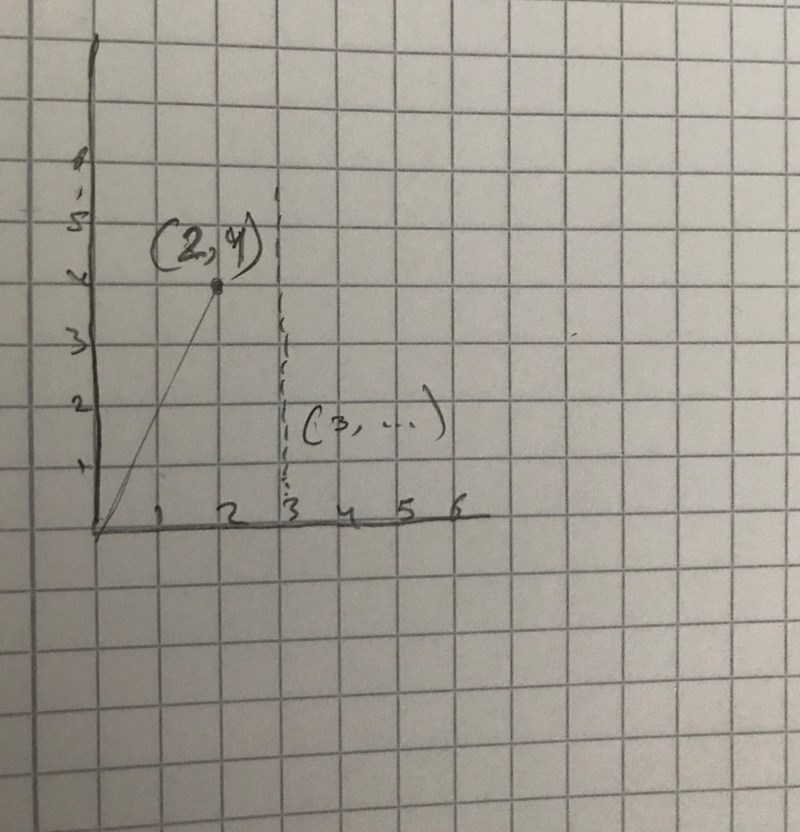 jag förstår bra den av uppgiften på koordinatsystemet.
jag förstår bra den av uppgiften på koordinatsystemet.
Men det är de båda avstånden (2,4)-(3,y) och (0,0)-(3,y) som ska vara lika.
Laguna skrev:Men det är de båda avstånden (2,4)-(3,y) och (0,0)-(3,y) som ska vara lika.
Så, om jag drar en linje från punkten (2,4) till punkten 3 på x-axeln y blir =0 och punkten blir (3,0).??
Hur stora är avstånden då?
Laguna skrev:Hur stora är avstånden då?
sedan vet inte
Freedom skrev:Laguna skrev:Men det är de båda avstånden (2,4)-(3,y) och (0,0)-(3,y) som ska vara lika.
Så, om jag drar en linje från punkten (2,4) till punkten 3 på x-axeln y blir =0 och punkten blir (3,0).??
Varför tror du att punkten skall ligga på x-axeln?
Avståndet från origo till punkten (3,y) skall vara lika stort som avståndet från punkten /2,4) till punkten (3,y).
Hur skriver du avståndet mellan de båda första punkterna med hjälp av avståndsformeln? Hur skriver du avståndet mellan de båda sista punkterna med hjälp av avståndsformeln? Sätt dessa båda uttryck lika med varandra. Om avstånden är lika, såär ävern kvadraterna på avstånden lika. Hur ser ekvationen ut när du har kommit så långt?
Smaragdalena skrev:Freedom skrev:Laguna skrev:Men det är de båda avstånden (2,4)-(3,y) och (0,0)-(3,y) som ska vara lika.
Så, om jag drar en linje från punkten (2,4) till punkten 3 på x-axeln y blir =0 och punkten blir (3,0).??
Varför tror du att punkten skall ligga på x-axeln?
Avståndet från origo till punkten (3,y) skall vara lika stort som avståndet från punkten /2,4) till punkten (3,y).
Hur skriver du avståndet mellan de båda första punkterna med hjälp av avståndsformeln? Hur skriver du avståndet mellan de båda sista punkterna med hjälp av avståndsformeln? Sätt dessa båda uttryck lika med varandra. Om avstånden är lika, såär ävern kvadraterna på avstånden lika. Hur ser ekvationen ut när du har kommit så långt?
Okej. om jag förstår bra det bör vara så
Svara på frågorna en i taget, eller skriv åtminstone vad det är du gör, så att vi kan förstå hur du tänker. Jag har t ex inte en aning om vad det är fför underlighet med 2 likhetstecken i som du skriver på första raden.
Smaragdalena skrev:Freedom skrev:Laguna skrev:Men det är de båda avstånden (2,4)-(3,y) och (0,0)-(3,y) som ska vara lika.
Så, om jag drar en linje från punkten (2,4) till punkten 3 på x-axeln y blir =0 och punkten blir (3,0).??
Varför tror du att punkten skall ligga på x-axeln?
Avståndet från origo till punkten (3,y) skall vara lika stort som avståndet från punkten /2,4) till punkten (3,y).
Hur skriver du avståndet mellan de båda första punkterna med hjälp av avståndsformeln? Hur skriver du avståndet mellan de båda sista punkterna med hjälp av avståndsformeln? Sätt dessa båda uttryck lika med varandra. Om avstånden är lika, såär ävern kvadraterna på avstånden lika. Hur ser ekvationen ut när du har kommit så långt?
Svar till första frågan: eftersom punkten på koordinatsystemet skriver (x,y) som (2,4) 2 är på x-axeln och 4 är på y-axeln. och därför när man säger (3,y) 3 måste vara på x- axeln och y eller vilka tal som helst ligger på y-axeln.
Nästa frågan, hur skriver jag avståndet mellan de båda första punkterna med hjälp av avståndsformeln?? det jag har redan från början visat. Tredje frågan, hur skriver jag avståndet mellan de båda sista punkterna med hjälp av avståndsformeln?? Det som jag kunde och förstått från uppgiften har redan visat, kanske saknar något men vet inte.
Du har skrivit att jag sätt de båda uttryck lika med varandra, jag har förstått på så sätt som jag har gjort här ner.
Hur ser ekvationen ut , som jag har skrivit och tänkt det ser (3-y)^2=(2-4)^2= 9-6y+y^2= 4-16+16 och sedan har förenklat.
Det är alls som jag har förstått av din info , uppgiften och min kunskap.
Du skrev en korrekt formel för avståndet mellan (3,y) och (2,4) lite högre upp. Kan du skriva en för avståndet mellan (3,y) och (0,0)?
Avståndsformeln är inget annat än Pythagoras sats.
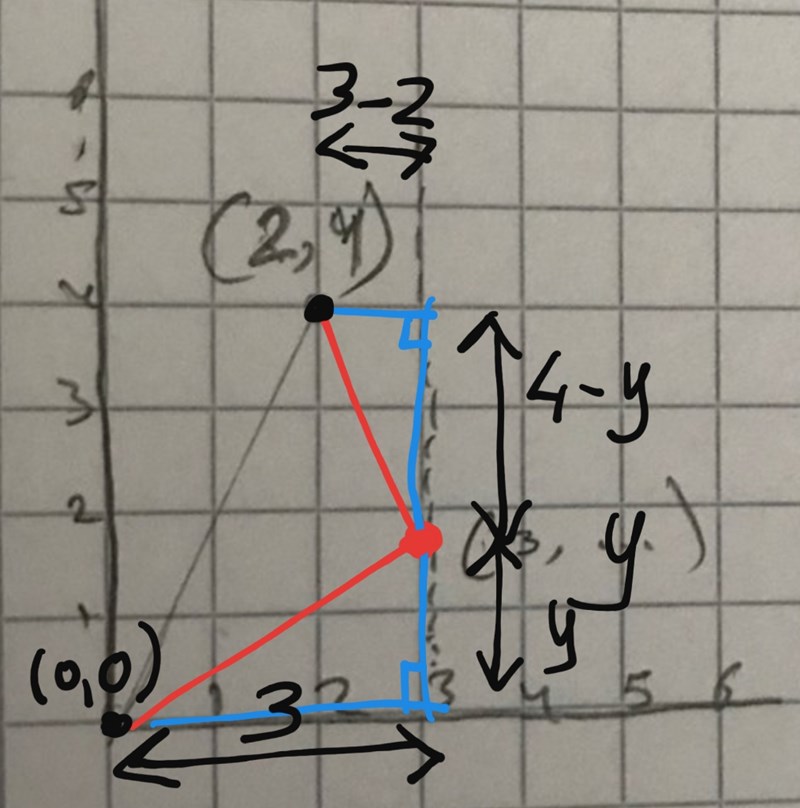
Titta på bilden.
Frågan gäller vilket vörde på y som gör att de två röda sträckorna är lika långa.
Du ser två rätvinkliga trianglar där de röda sträckorna är hypotenusor och där jag har angivit katetrarnas längder.
Kommer du vidare då?
Svar till första frågan: eftersom punkten på koordinatsystemet skriver (x,y) som (2,4) 2 är på x-axeln och 4 är på y-axeln. och därför när man säger (3,y) 3 måste vara på x- axeln och y eller vilka tal som helst ligger på y-axeln.
Punkten (3,y) ligger på x-axeln om och endast om y=0.






