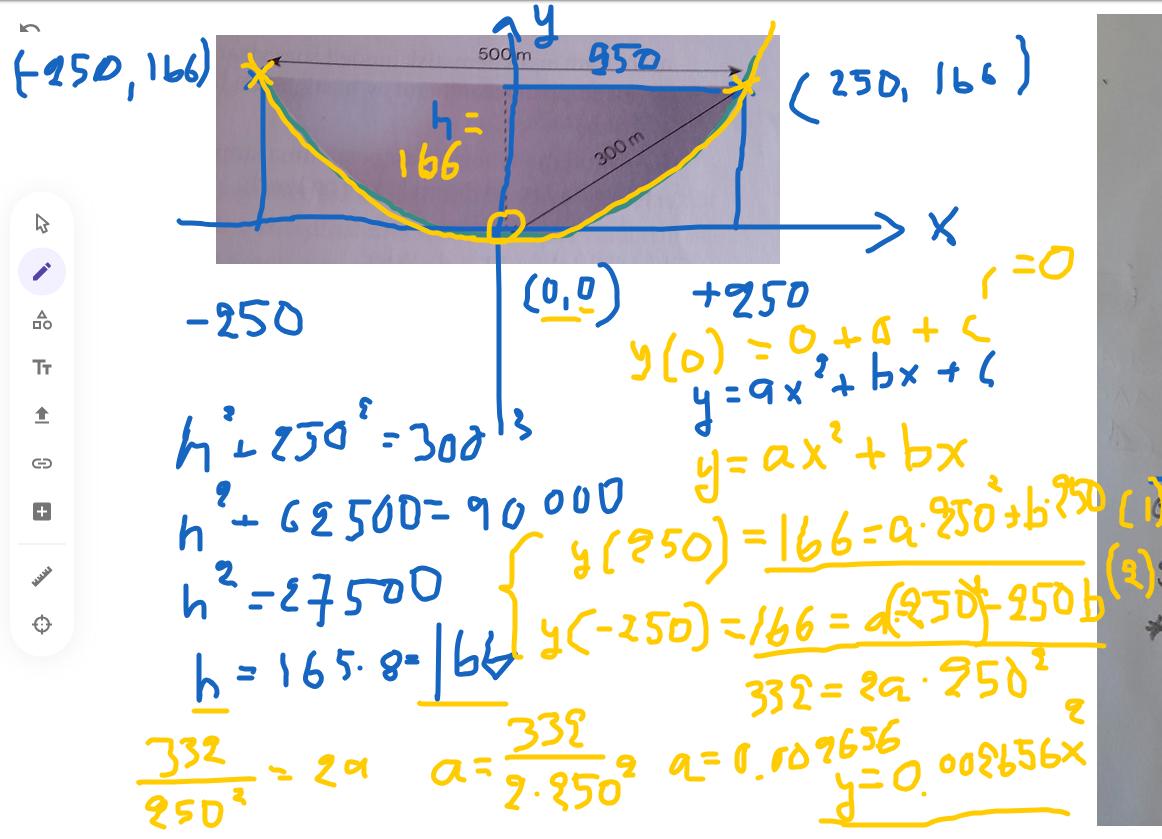
Radioskåpet FAST
kan man använda pythagoras sats ?
så här
sedan tillämpar jag k-form
k
Det låter bra, men 250 har blivit 200 i din uträkning.
Det står inte var de vill ha x-axeln, men jag skulle lägga den vid nedersta punkten, och då blir uttrycket bara kx2.
Du har rätt. Det var ett slarvfel.
Om vi lägger botten i origo;
y(x)=kx^2
y(250)=sqrt(300^2-250^2)
k 250^2=50sqrt(11)
k=sqrt(11)/1250
Alt. 1
y(x)=kx(x-500) med y(250)=-sqrt(300^2-250^2) vilket ger samma svar.
Alt. 2
y(x)=kx^2-sqrt(300^2-250^2) med y(250)=0 vilket ger samma svar.
Trinity har du en bild ?
Att "botten ligger i origo" är samma placering av koordinatsystemet som i denna din andra tråd om chipset.
Utgå från det och försök att rita en liknande bild, men i det här fallet med endast en parabel.
Visa din bild.
Yngve skrev:Att "botten ligger i origo" är samma placering av koordinatsystemet som i denna din andra tråd om chipset.
Utgå från det och försök att rita en liknande bild, men i det här fallet med endast en parabel.
Visa din bild.
Jag tolkar uppgiften så här. Men, fick fel svar

Tycker du att kurvan skär x-axeln när x = 500?
ja, eller vad är det för "fel" med det ?
är inte koordinaterna (500,250) ?
Den gula punkten uppe till höger har inte koordinaterna (500,250)
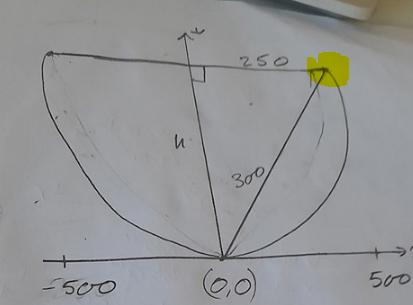
Däremot (250,h)
(500, 250) ligger på kurvan, ja, men det ligger inte på x-axeln.
Laguna skrev:(500, 250) ligger på kurvan, ja, men det ligger inte på x-axeln.
Nej, punkten (500,250) ligger långt till höger om kurvan.
Arup skrev:ja, eller vad är det för "fel" med det ?
Jag har tagit din bild och markerat x-axeln med blått.
Parabeln skär x-axeln på ett enda ställe, nämligen i origo.
Jag har markerat detta med en röd punkt.
Dessutom är dina x-koordinater fel. Som du har ritat det så har radioteleskopet en diameter på 1000 meter, inte 500 meter.

är det då en dubbelrot ?
Smaragdalena skrev:Laguna skrev:(500, 250) ligger på kurvan, ja, men det ligger inte på x-axeln.
Nej, punkten (500,250) ligger långt till höger om kurvan.
Jaha, inte ens det.
Arup skrev:Trinity har du en bild ?
De 3 olika funktionerna;
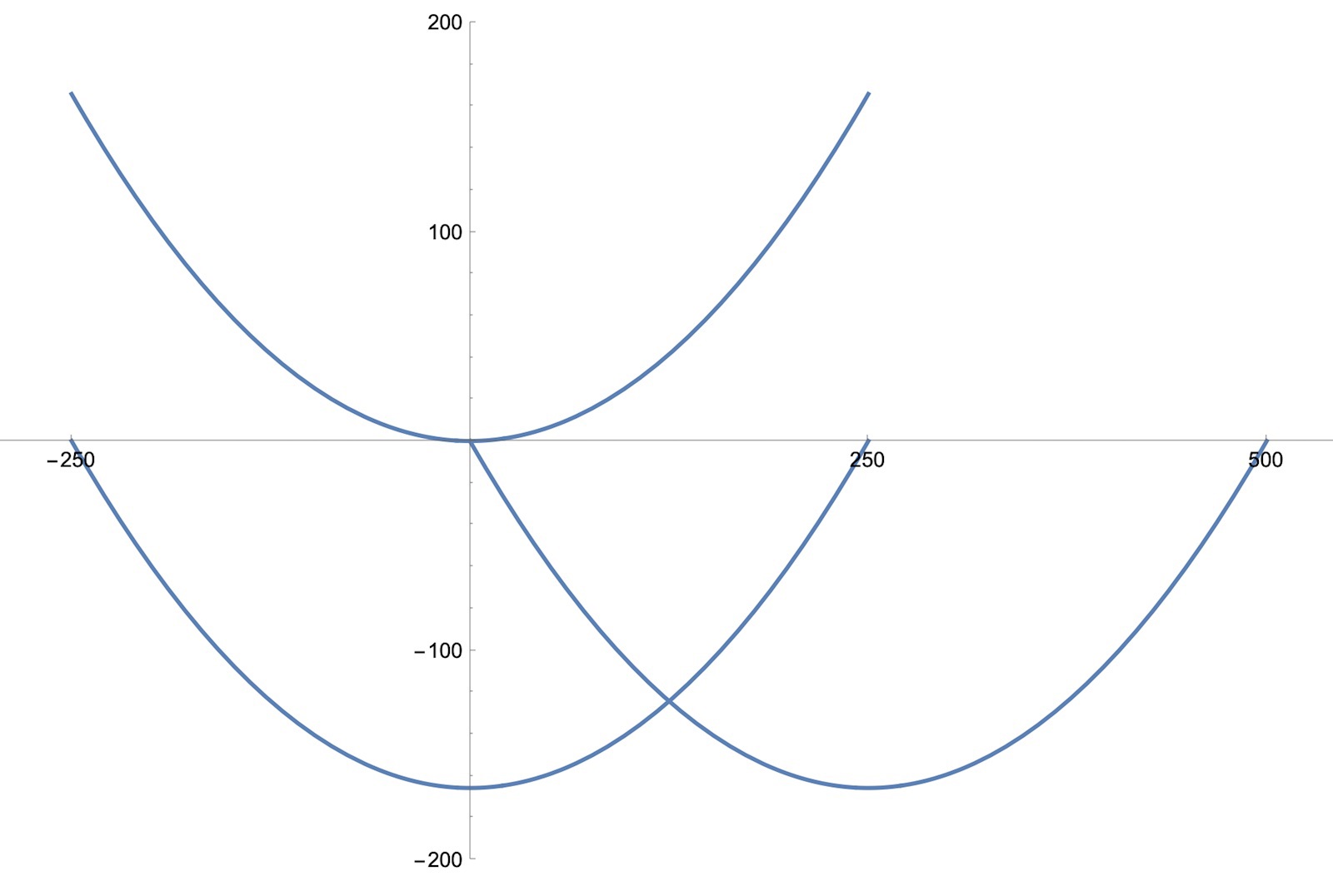
hur blir det 3 olika funktioner ?
Arup skrev:hur blir det 3 olika funktioner ?
Endast en, men jag visade 3 olika lösningar på problemet.
Arup skrev:är det då en dubbelrot ?
Låt f(x) vara den andragradsfunktion som motsvarar parabeln.
Ekvationen f(x).= 0 har då en dubbelrot vid x = 0.
Var det så du menade?
Yngve jag menar att parabeln endast skär x-axeln på ett ställe
Arup skrev:Yngve jag menar att parabeln endast skär x-axeln på ett ställe
Ja, det stämmer.
Jag gjorde ett eget försök

Bra början, snyggt och prydligt.
Men du bör alltid kontrollera dina delresultat.
Har du t.ex. kontrollerat att den gulmarkerade ansatsen stämmer?

oj det borde vara
eller ?
Du använder den faktoriserade formen y = k(x-x1)(x-x2).
Fundera på vad x1 och x2 står för i det uttrycket.
Stämmer det i ditt fall med parabeln?
nej, de borde då väl vara så här :
y=k(x+250)(x-250)
Tönk efter. Vad står x1 och x2 för i uttrycket y = k(x-x1)(x-x2)?
Yngve skrev:Tönk efter. Vad står x1 och x2 för i uttrycket y = k(x-x1)(x-x2)?
Är det inte mina nollställen ?
Arup skrev:
Är det inte mina nollställen ?
Jo, det stämmer.
Och vilka är parabelns nollställen?
Enligt min bild så är väl
Är det verkligen ett nollställe?
Ett nollställe betyder en punkt där funktionen har värdet 0, dvs där grafen skär x-axeln.
Skär grafen x-axeln vid x = -250 och vid x = 250?
ja, eftersom dess dimater är väl 500m
så borde då det bli 250-(-250) =500 eller ?
OK om vi säger så här då:
Se bild, vid vilket/vilka x-vörden skär/nuddar parabeln x-axeln? Kan du markera I bilden?

i origo
Ja, det stämmer. Där är x = 0, eller hur?
Det betyder att I detta fallet är x1 = x2 = 0.
Eller varför inte läsa om tråden från början, vi har redan gått igenom och rätat ut frågetecknen kring nollställen, dubbelrot osv en gång.
Jag förstår men det är väl kul i sig att lösa uppgiften med säkerhet
Om du menar att lösa uppgiften igen för att repetera så håller jag med dig fullständigt. Dessutom är det nyttigt.
Behöver du mer hjälp framåt här?
Kanske, men kan du kika om mina nya lösning innehåller några slarvfel.
Jag kommer troligtvis att skicka en ny lösning ikväll
Arup skrev:Kanske, men kan du kika om mina nya lösning innehåller några slarvfel.
Jag kommer troligtvis att skicka en ny lösning ikväll
OK.
Jag vet inte varför det blir fel på sista raden

Arup skrev:Jag vet inte varför det blir fel på sista raden
EDIT: Sorry. Jag läste jätte fel. På de sista raderna, ska du inte ha x=250 för att f(250) = 50*sqrt(11)?
Så blir det
k=
Arup skrev:Så blir det
k=
Nej. Om du vet att funktionen är f(x) = k(x)^2, och f(250) = 50*sqrt(11), kan du nu lösa för k? Jag antar att funktionen är med respekt till x, dvs k är en konstant?
jag kan ju bara dividera x^2 i båda leden för att isolera k
Arup skrev:jag kan ju bara dividera x^2 i båda leden för att isolera k
Det är inte det jag menar...det är ju rätt men det leder ingenstans.
om du sätter x = 250 i uttrycket k*(x^2), så får du k*(250)^2. Håller du med mig på det?
ja och ja
Så om du nu har:
50*sqrt(11) = k(250)^2, kan du nu lösa för k? Vad vi just gjorde precis var att sätta x=250 för funktionen: f(x) = k(x)^2. Du vet också att f(250) är lika med 50*sqrt(11).
ok så då har jag alltså koordinaten
Arup skrev:ok så då har jag alltså koordinaten
Ja, och det tillsammans med ger dig nu ekvationen , dvs
Är du med på det?
(Se även svar #6 av Trinity2)
jag men Yngve du sa att radioskåpet hade en dubbel rut i origo så därför var jag förvirrad i #46
Arup skrev:jag men Yngve du sa att radioskåpet hade en dubbel rut i origo så därför var jag förvirrad i #46
Ja.
- Funktionen f(x) = kx2 har endast ett nollställe, nämligen i origo.
- Ekvationen kx2 = 0 har en dubbelrot i origo.
Du har alltså satt upp funktionsuttrycket korrekt i svar #46, här:

Så har jag löst uppgiften ?
Nej, jag ser inte att du har skrivit rätt svar någonstans.
Men i svar #46 är allt rätt förutom de sista två raderna.
Är det rätt nu ?

Jag undrar dock om jag hade fått full poäng för min lösning om denna uppgift skulle förekomma på ett prov
Jag tror tyvärr inte det. Det är ett par problem med lösningen.
1. Du skriver "... där ", men sambandet gäller ju för alla i intervallet :

2. Du bör inte avrunda k-värdet, men om du ändå gör det så måste du använda istället för = här:

3. Du bör förenkla k-värdet så långt som möjligt, dvs skriva här:

Vad är det för fel med lösningen Yngve ?
jag fick 50* eftersom detta är inget närmevärde utan ett exakt svar
Arup skrev:Vad är det för fel med lösningen Yngve ?
jag fick 50* eftersom detta är inget närmevärde utan ett exakt svar
Det är inte så du formulerar ditt svar:

Varför det ?
Hur kan jag formulera mitt svar bättre?
I inlägg #25 fick Sten och jag samma svar
Arup skrev:Varför det ?
Jag förstår inte frågan.
Arup skrev:Hur kan jag formulera mitt svar bättre?
Förslag:

I inlägg #25 fick Sten och jag samma svar
En petig lärare kan mycket väl ge poängavdrag för att du anger ett närmevörde utan att skriva
Ok jag var nästan där men rent matematiskt så är våra lösningar samma. Det är bara att du skrev svaret mer ”tydligare” dvs I exakt form
Arup skrev:Ok jag var nästan där men rent matematiskt så är våra lösningar samma. Det är bara att du skrev svaret mer ”tydligare” dvs I exakt form
Javisst, du var nästan där.
Men det kan vara bra att fortsätta att be om lösningsförslag som du sedan kan härma.