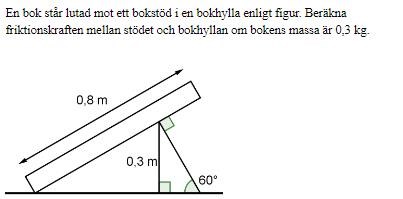
Räkneuppgift - kraft

Min lösning:

Jag har försökt lösa denna uppgift, har ingen facit. Har jag tänkt rätt?

Hur löser man annars uppgiften?

Jag tror inte att 0,3g * 0,4 = F₂ * 0,8 stämmer. Kanske är det bättre att rita alla krafter.

Var är F₂? Var är mg?

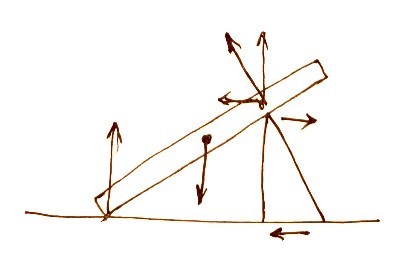
Vilken är F₂?

mg blir ju då kraften av boken alltså 0,3*g

men f₂är det lite svårt, det är ju den kraft som är vinkelrät mot momentanpunkten.

Kraften medurs måste ju vara kraften av hela boken multiplicerad med momentanarmen.

Kraften moturs är ju då den uppdelade kraften högst upp och då är det ju endast Fy som räknas

Blir det då att

0,3*g*0,4= F₂ * 0.8

där F₂ är då f*sin 30?

Jag är fortfarande inte helt säker på vad du kallar F₂. Det kan inte vara vinkelrätt mot en punkt, det är vinkelrätt mot boken. (Jag kallar det bara F, eftersom vi inte har någon F₁)

Medurs och moturs: Dessa är F_y och F_x, komponenterna i F.
Nu har jag gett ett namn till allt som räknas.

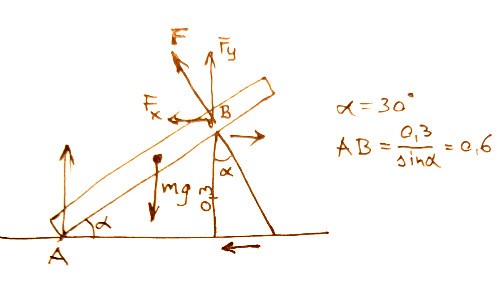
Så vi kan bestämma F_y från momentumekvationen för punkt A:

$m \cdot g \cdot 0, 4 \cdot \cos α = F_{y} \cdot 0, 6 \cdot \cos α$ (eftersom AB = 0,6)

$0, 3 \cdot g \cdot 0, 4 = F_{y} \cdot 0, 6$

F_y = 1,962N

------

$F_{x} = F_{y} \cdot t g α = 1, 133 N$

Och det är den kraft som friktionen borde ge oss.

Macilaci skrev:
Jag är fortfarande inte helt säker på vad du kallar F₂. Det kan inte vara vinkelrätt mot en punkt, det är vinkelrätt mot boken. (Jag kallar det bara F, eftersom vi inte har någon F₁)

Medurs och moturs: Dessa är F_y och F_x, komponenterna i F.
Nu har jag gett ett namn till allt som räknas.

Så vi kan bestämma F_y från momentumekvationen för punkt A:

$m \cdot g \cdot 0, 4 \cdot \cos α = F_{y} \cdot 0, 6 \cdot \cos α$ (eftersom AB = 0,6)

$0, 3 \cdot g \cdot 0, 4 = F_{y} \cdot 0, 6$

F_y = 1,962N

------

$F_{x} = F_{y} \cdot t g α = 1, 133 N$

Och det är den kraft som friktionen borde ge oss.

För helhetens skull (men utan att ha någon betydelse för svaret) så borde det finnas en horisontell friktionskraft på boken vid A också, eller hur?

Ja, det är sant. Jag borde ha ritat en kraft till, för boken är ju i vila.

Ojdå! Detta förstör själva problemet.
Varför antar vi att det finns friktion i punkt A, men inte i punkt B?
Om vi har friktion varken i punkt A eller i punkt B, så börjar boken glida ner.
Om vi har friktion i punkt B är hela beräkningen fel.

Jag var inne på samma tankegång, jag får inte riktigt ihop det...

Problemet är obestämt. Boken "står", så vi måste anta att friktion finns någonstans. Men svaret beror på hur friktionen delas mellan A och B.

Så hur ska man tänka då?

Antar att svaret inte är 1,33N.

Delar man in friktionen då i en y-komposant och en x-komposant

som sin och cos

Nej. Friktionen har bara x komponent. Men det går inte att beräkna friktionskraften mellan stödet och hyllan.

Svaret är 1,33N bara om man antar att det inte finns friktion i punkt A, men i uppgiften säger man ingenting om det.

Svara Avbryt

Visa senaste svar