Rang och spår för "engångsmatriser"

Jag tror att påståendet är fel eftersom $1\ne 2.$ 

Red.: Jag glömde att det handlar om engångsmatriser. För generella matriser tror jag att påståendet är fel.

Låt v vara en godtycklig vektor i rummet $V = R^{n \times n}$. Då ska det alltså gälla att

$A^2 v = Av$ eller ekvivalent med $A(A - I)v = 0$. Det senare är intressant eftersom detta betyder att antingen så är $(A - I)v = 0$ dvs att v är en egenvektor med egenvärde 1, eller så är $(A - I)v$ en egenvektor till Amed egenvärde 0. 

Detta antyder en induktiv process liknande Gram-Smidt  i vilket vi kan separera ut alla egenvektorer till A och se att de antingen har egenvärde 1 eller 0.

0. Definiera två mängder M och N, där M kommer vara en mängd innehållandes egenvektorer med egenvärde 1 och N vara en mängd som innehåller egenvektorer med egenvärde 0.

1. Ta en vektor v ur V. Om v är en egenvektor med egenvärde 1 så lägg den i M och tag det ortogonala komplementet av alla vektorer i V till v, dvs ta bort alla vektorers komponenter som är parallella med v. Vi uppdaterar V <- V_{v}

Om v inte är en egenvektor med egenvärde 0 så lägg (A - I)v i mängden N och projicera bort den vektorn från V. 

2. Upprepa steg 1, där varje upprepning reducerar V:s dimension med 1,  tills dess att V har reducerats till dimension 0. 

3. Eftersom processen tog n steg så har vi funnit s egenvektorer med egenvärde 1 och t egenvektorer med egenvärde 0, där s + t = n. 

(En möjlig invändning är att (A - I)v kanske inte är är oberoende av en vektor som redan placerats i M eller N och i skrivande stund kan jag inte utesluta det. Jag känner mig dock dugligt säker på saken men välkomnar ett motbevis)

Nu har vi funnit att matrisen har s egenvektorer med egenvärde 1 och t egenvektorer med egenvärde 0.

Spåret av men matris är summan av dess egenvärden vilket blir tr(A) = s och rangen av en (diagonaliserbar) matris är antalet egenvärden som inte har 0 som egenvärde vilket också är s, rang(A) = s.

Alltså

tr(A) = rang(A)

(Notera att vi faktiskt kan behöva använda matrisen (eg. A - I) upp till n-1 gånger för att få ut egenvektorerna så så en enda gång räcker inte)

Jag förstår inte din algoritm. Vad händer i steg 1 om vi inte tar en vekter med egenvärde 1?  Om vi tar en med egenvärde 1, varför finns det egenvektorer i ortogonala komplementet?

Stycke två i steg 1 borde säga att om v inte är en egenvektor med egenvärde 1 (står 0) så är (A-I)v en egenvektor med egenvärde 0. 

 Argumentet har som sagt en outforskad del gällande oberoendet mellan egenvektorerna man plockar ut och har önnu inte fixat det hela. 

Kruxet ligger egentligen i att det för mitt inte öga är uppenbart att sådana matriser är diagonaliserbar i vilket fall satsen faller ut naturligt men utan att se att sådana säg är symmetriska eller i någon diagonaliserbar klass så blir algoritmen är ett försök att komma fram till att den är diagonaliserbar.

Du kan ta en genväg genom att matrisen (eller en normal operator) är diagonaliserbar om den algebraiska multipliciteten är lika med den geometriska multipliciteten. Dimensionen för värderummet,  V(P), och dimensionssatsen garanterar att n-rang(A) är antalet "nollrader" och en reell idempotent matris är alltså alltid diagonaliserbar.

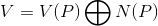
Hur bestämmer du multipliciteterna isf i detta fall?

SeriousCephalopod skrev:

Hur bestämmer du multipliciteterna isf i detta fall?

 Eftersom den karaktäristiska ekvationen är av grad n om A är en nxn-matris, så har enligt algebrans fundamentalsats A exakt n egenvärden, om man räknar med (algebraisk) multiplicitet. Vi låter dimensionen av värderummet till A vara $\rang(A)=\dim V(A)=r$.

Låt oss anta att (n-r) st av dessa egenvärden antar värdet 0. Egenvektorer hörande till dessa egenvärden ligger naturligtvis i N(A), ty $Ae_i=0e_j=0$. Resterande egenvektorer, dvs r stycken, måste då ligga i V(A), ty $Ae_ j=e_j$  och $n=\dim\,N(A)+\dim\, V(A)=(n-r)+r$ enligt dimenssionssatsen.

Förövrigt "brukar" man använda egenskaper hos minimalpolynomet för att visa att en idempotent matris är diagonaliserbar (med egenvärden 0, 1).

Men man kan också gå "direkt", om för något egenvärde den geometriska multipliciteten är strikt mindre än den algebraiska kan inte summan av egenrummens dimensioner vara lika med det karakteristiska polynomets gradtal. Om vi delar upp rummet som en direkt summa (se V ovan) följer därför att varje egenvärdes geometriska multiplicitet är lika med dess algebraiska. (jmfr spektralsatsen för normala operatorer).

--------------------------------------------------------------------------------------------------------------

Slutligen kan man kan använda determinanter också! Om determinanten $\det (A-\lambda E)$ utvecklas ser vi att

$\det (A-\lambda E)=\begin{vmatrix}a_{11}-\lambda& a_{12}&...&a_{1n}\\a_{21}&a_{22}-\lambda&...&a_{2n}\\--&--&--&--\\a_{n1}&a_{n2}&...&a_{nn}-\lambda\end{vmatrix}=$

$=(-1)^n\lambda^n+(-1)^{n-1}(a_{11}+...+a_{nn})\lambda^{n-1}+...+\det A$

Vi inser också att

$\det(A-\lambda E)=(-1)^n(\lambda-\lambda_1)...(\lambda-\lambda_n)=$

$=(-1)^n\lambda^n+(-1)^{n-1}(\lambda_1+...+\lambda_n)+...+\lambda_1...\lambda_n$

Ur vilken vi bland annat kan identifiera

$\lambda_1+\lambda_2+...+\lambda_n=a_{11}+a_{22}...+a_{nn}=Tr(A)$

Där vi använt beteckningen Tr(A) för summan av A:s diagonalelement (spåret)

I vårt fall är summan $\lambda_1+...\lambda_n=rang(A)$ och därför måste $rang(A)=Tr(A)$

Kul med all respons! Jag avvaktar tills i morgon med mitt eget förslag, men ger två kommentarer så länge.

@Albiki: Att konstatera att påståendet är orimligt för generella $n\times n$-matriser är definitivt en bra början (och kanske något jag borde ha påpekat redan i trådstarten för att få påståendet att kännas mer spektakulärt).

Nu när jag tänker efter lite mer är det ju verkligen helt absurt att det för generella matriser $A\in\mathbb{R}^{n\times n}$ skulle gälla att $\mathrm{rang}(A)=\mathrm{tr}(A)$. Vänsterledet är ju ett heltal mellan $0$ och $n$, medan $\mathrm{tr}(A)$ i allmänhet inte ens är ett heltal.

Så om påståendet gäller för engångsmatriser, så måste det vara något med egenskapen $A^2=A$ som rejält begränsar vad $\mathrm{tr}(A)$ kan vara. Och en sådan insikt kan definitivt vara en bra ingång, både för att leta motexempel eller som inspiration för ett bevis.

 @Guggle: Jag måste säga att det är lite svårt att följa dina resonemang. I princip håller jag med om det du skriver, men det är många omotiverade påståenden och infallsvinklar på en gång. Funderar främst på följande punkter:

• I ditt första inlägg konstaterar du att nollrummet för en matris $A\in\mathbb{R}^{n\times n}$ har dimensionen $$n-\mathrm{rang}(A). Hur menar du att det medför att engångsmatriser är diagonaliserbara?
• Du påstår även att $\mathbb{R}^{n\times n}$ är en direkt summa av värderummet och nollrummet, men jag tycker inte det framgår varför det skulle vara sant.
• I ditt andra inlägg konstaterar du att $A$ har $n$ stycken (komplexa) egenvärden, räknade med algebraisk multiplicitet, och du skriver sedan att du antar att $n-r$ av dessa egenvärden är 0 (där $r$ är rangen för $A$). Men för att ditt argument ska fungera måste du väl visa att detta verkligen är sant?
• I ditt tredje inlägg härleder den klassiska, trevliga likheten $\mathrm{tr}(A)=\lambda_1+\cdots+\lambda_n$. Men hur vet du att summan av egenvärdena i sin tur är lika med rangen?
• Du nämner även normala operatorer och spektralsatsen på ett par ställen. Vad är kopplingen mellan detta och engångsmatriser?

Använd rankfaktorisering. En matris A med rank R kan skrivas som en produkt av två matriser, P och Q där P har full rank i kolonnrummet och Q har full rank i radrummet. Från detta följer att P har en vänsterinvers och Q har en högerinvers och att $P^{-1}PQQ^{-1} = I$ där I är identiteten som är en R x R . Vi kan då skriva att

$A = A^2 \Rightarrow PQPQ=PQ \Rightarrow QP = I$

där vi använder oss av inverserna från vänster och höger. Från detta ser vi då att

$Tr(A) = Tr(QP) = Tr(I) = R = rank(A)$

där vi använt oss av att $Tr(PQ) = Tr(QP)$.

(Sorry att jag inte latexade allt, jag tål inte att göra det för mycket på windowsdatorer)

 @Guggle: Jag måste säga att det är lite svårt att följa dina resonemang. I princip håller jag med om det du skriver, men det är många omotiverade påståenden och infallsvinklar på en gång. Funderar främst på följande punkter:

Oj, då har jag misslyckats i min pedagogiska gärning!. Nu var mina inlägg iofs inte avsedda som formella bevis utan som tips om hur man kan gå till väga, men jag förutsätter du håller med om följande resultat från linjär algebra:

• En självadjungerad operators egenvärden är reella. (Och en unitär operators egenvärden är komplexa tal med absolutbelopp 1).
• En godtycklig operators olika egenrum är linjärt oberoende.
• Egenrummen för normala operatorer är parvis ortogonala och kan alltså uttryckas som en summa.

Nu tycker jag att SeriousCephalopod på ett framgångsrikt sätt redan visat att egenvärden till en idempotent matris antingen är 0 eller 1, men låt $\mathbf{e}_1, ..,\mathbf{e}_r$ utgöra en linjärt oberoende bas till värderummet V(A).  Låt $\mathbf{x}_i$ vara r st vektorer i värderummet för vilka

$A\mathbf{x}_i=\mathbf{e}_i$

Multiplicera med A och utnyttja $A^2=A$

$A^2\mathbf{x}_i=AA\mathbf{e}_i$

$A\mathbf{e}_i=\mathbf{e_i}$

Basen $\mathbf{e}_i$ är alltså r stycken linjärt oberoende egenvektorer till A med egenvärdet 1 som spänner V(A).

Den geometriska och algebraiska multipliciteten för egenvärdet 1 är det samma som dimensionen för värderummet V(A).

Summan av egenvärden (de andra n-r är ju 0) $\lambda_1...+\lambda_n=r$

Eftersom $rang(A)=dim\,V(A)=r$ gäller alltså $rang(A)=Tr(A)$. Är du med på det?

Baserat på punkterna ovan kan man också visa att om A verkar på det n-dimensionella rummet V så är

Och den idempotenta operatorn A är diagonaliserbar, naturligtvis gäller dimensionssatsen med dim V(A) = r att dim N(A) = n-r (egenskaper vi inte behöver men som kan hjälpa den som faktiskt vill diagonalisera A).

@Guggle: Tack för förtydligandet! Dock är jag fortfarande förvirrad över hur självadjugerade/normala operatorer och spektralsatsen kommer in i bilden?

oggih skrev:

@Guggle: Tack för förtydligandet! Dock är jag fortfarande förvirrad över hur självadjugerade/normala operatorer och spektralsatsen kommer in i bilden?

 Jag ska kanske vara lite mer tydlig med vad som är tips och ledtrådar i framtiden. Som jag visat behöver man inte diagonalisera A för att visa $rang(A)=Tr(A)$. Och man behöver  inte använda normala operatorer eller spektralsatsen för att visa det.

Det jag försökte ge  tips om var två andra möjliga sätt att visa att V kan skrivas som en direkt summa av N(A) och V(A) där dimensionen av V(A) = r och dim N(A) = n-r;  1) minimalpolynomet (vad delar vad?) eller 2) skriva om A på ett lämpligt sätt samt utnyttja spektralsatsen (en ledtråd här kan vara att börja med att studera om det finns en unitär operator U så att $A=UR$).

Jag hänger med på hur normala operatorer kommer in i bilden, det som jag som sagt inte hänger med på är vad beviset är för att operatorn är normal (även om jag såklart vet att så är fallet). 

För mina ögon dyker faktumet att matrisen är normal/diagonaliserbar plötsligen bara upp efter att Guggle kommenterat på multipliciteterna men utan att det görs en konkret hänvisning till $A^2 = A$ egenskapen som nu endast använd för att visa att egenvärdena är 0 eller 1.

Kruxet ligger som sagt i att vi endast vet att geometriska multpliciteten är mindre än den algebraiska men inte, utifrån texten, att de är lika.

Tag följande matris som vare sig är självadjungerande eller normal men som har egenvärden 0 eller 1 som ett exempel på vad som skulle kunna hända om multipliciteterna inte var lika.

$\begin{pmatrix}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0\end{pmatrix}$ 

Här gäller alltså att karaktäristiska polynomet är $\lambda^2(\lambda - 1)^2$ där det för 1-egenvärdet gäller att algebraiska multipliciteten är 2 och att geometriska multipliciteten är 2 men för 0-egenvärdet så är algebraiska multiplicteten 2** och geometriska multipliciteten 1 så vi får spår = 2 och rang = 3.

Från detta exempel kan vi generalisera oss till "Om en generell matris har egenvärden 0 eller 1 så gäller $tr(A)\leq rang(A)$"  men inte likheten.

Så hur motiverar vi, utifrån att $A^2 = A$, att geometriska multipliciteten för 0-egenvärdet är lika med den algebraiska multipliciteten för 0-egenvärdet?**

EDIT: På **-ställena är det möjigt att min användning av geometrisk multiplicitets-begreppet inte är 100 korrekt då jag är ovan med att använda det men förhoppningsvis framgår fokuset ändå. 

emmynoether skrev:

Använd rankfaktorisering. En matris A med rank R kan skrivas som en produkt av två matriser, P och Q där P har full rank i kolonnrummet och Q har full rank i radrummet. Från detta följer att P har en vänsterinvers och Q har en högerinvers och att $P^{-1}PQQ^{-1} = I$ där I är identiteten som är en R x R . Vi kan då skriva att

$A = A^2 \Rightarrow PQPQ=PQ \Rightarrow QP = I$

där vi använder oss av inverserna från vänster och höger. Från detta ser vi då att

$Tr(A) = Tr(QP) = Tr(I) = R = rank(A)$

där vi använt oss av att $Tr(PQ) = Tr(QP)$.

(Sorry att jag inte latexade allt, jag tål inte att göra det för mycket på windowsdatorer)

 Jag blir besviken på de andra deltagarna i tråden när de helt ignorerar ditt inlägg EmmyNoether.

Ditt inlägg är helt klart den mest eleganta lösningen på problemet; kort och koncist, utan en massa svada om egenvärden, geometriska multipliciteter, algebraiska multipliciteter, självadjungerade normala operatorer, karakteristika polynom och jag vet inte vad. Det finns lösningar och så finns det lösningar.

Albiki skrev:

emmynoether skrev:

Använd rankfaktorisering. En matris A med rank R kan skrivas som en produkt av två matriser, P och Q där P har full rank i kolonnrummet och Q har full rank i radrummet. Från detta följer att P har en vänsterinvers och Q har en högerinvers och att $P^{-1}PQQ^{-1} = I$ där I är identiteten som är en R x R . Vi kan då skriva att

$A = A^2 \Rightarrow PQPQ=PQ \Rightarrow QP = I$

där vi använder oss av inverserna från vänster och höger. Från detta ser vi då att

$Tr(A) = Tr(QP) = Tr(I) = R = rank(A)$

där vi använt oss av att $Tr(PQ) = Tr(QP)$.

(Sorry att jag inte latexade allt, jag tål inte att göra det för mycket på windowsdatorer)

 Jag blir besviken på de andra deltagarna i tråden när de helt ignorerar ditt inlägg EmmyNoether.

Ditt inlägg är helt klart den mest eleganta lösningen på problemet; kort och koncist, utan en massa svada om egenvärden, geometriska multipliciteter, algebraiska multipliciteter, självadjungerade normala operatorer, karakteristika polynom och jag vet inte vad. Det finns lösningar och så finns det lösningar.

Jag satt och fnissade lite för mig själv faktiskt, "jaha, jag antar att mitt bidrag inte gills då". Haha! :)

Upphör diskussionen av ett bevis för att ett annat har formulerats?

Men jovisst emmynoethers bevis var mycket bra och överaskande kompakt. 

SeriousCephalopod skrev:

Upphör diskussionen av ett bevis för att ett annat har formulerats?

Men jovisst emmynoethers bevis var mycket bra och överaskande kompakt. 

 Givetvis inte, jag tyckte mest det var roligt att mitt inlägg gled in mellan era där och passerade ganska obemärkt. Jag följer er diskussion också, även om jag inte riktigt ser hur beviset kan formas runt det. Det kanske klarnar!

@EN: Ditt bidrag gills i högsta grad! Detta var första gången jag stötte på rang-faktorisering (så jag var tvungen att fundera lite), men det är ju verkligen en riktigt fiffig typ av matrisfaktorisering, som (vilket framgår av ditt bevis!) verkligen är som klippt och skuren för det här problemet. Så tack för ett kort, tydligt och nästan maximalt lätttillgängligt bevis (man behöver i princip bara förstå vad rang och spår betyder!).

@Guggle: Tack igen! Jag ser vad du menar med minimalpolynomet (riktigt kort och koncist argument om man känner till att diagonaliserbarhet följer om minimalpolynomet kan uttryckas som en product av distinkta förstagradare), men approachen med spektralsatsen förstår jag fortfarande inte. Orkar du (eller någon annan som är med på noterna) ge fler ledtrådar eller en skiss av det bevis du har i åtanke? :)

Här kommer mitt eget lösningsförslag, som i princip är en variant av det som SC och Guggle redan har föreslagit.

Påstående. Om $A\in\mathbb{R}^{n\times n}$ uppfyller likheten $A^2=A$, så gäller att $\mathrm{rang}(A)=\mathrm{tr}(A)$.

Bevis. Precis som er andra tycker jag det skulle kännas trevligt att göra något slags basbyte, sådant att både rangen och spåret blir enkelt att läsa av (notera att både rangen och spåret är bas-oberoende egenskaper hos en linjär avbildning). Det bästa vore om man kunde diagonalisera, så låt oss göra ett försök!

Första steget är då att fundera på vad $A$ kan tänkas ha för egenvärden (om det ens finns några). Vi låter därför $v\in\mathbb{R}^n\setminus\{0\}$ vara en hypotetisk egenvektor med egenvärde $\lambda\in\mathbb{R}$, och noterarar att vi å ena sidan får

     $A^2v=A(Av)=A(\lambda v)=\lambda (Av)=\lambda^2v\,,$

och å andra sidan (eftersom $A$ är en engångsmatris) får

     $A^2v=Av=\lambda v\,.$

Detta kan bara inträffa om $\lambda^2=\lambda$, dvs. om $\lambda=0$ eller $\lambda=1$. Så detta är tydligen de enda möjliga egenvärdena för $A$.

För att lyckas diagonalisera $A$ måste vi nu koka ihop en bas för $\mathbb{R}^n$ bestående av egenvektorer ur (de möjligen triviala) egenrummen för 0 respektive 1.

En bra början kan vara att fundera på vad dessa egenrum egentligen är för något. Som vanligt är egenrummet för 0 detsamma som nollrummet:

     $V_0=\{v\in\mathbb{R}^n:Av=0v=0\}=\mathrm{null}(A)$

och eftersom $A$ är en engångsmatris är egenrummet för 1 lika med kolumnrummet (tänk på vänster- respektive högerinklusionen var för sig):

     $V_1=\{v\in\mathbb{R}^n:Av=1v=v\}=\mathrm{col}(A)\,.$

Låt oss nu ta en bas $\mathcal{B}_0=\{u_1,\ldots,u_s\}$ för $\mathrm{null}(A)$, där $s=\mathrm{dim}\,\mathrm{null}(A)$, och en bas $\mathcal{B}_1=\{v_1,\ldots,v_r\}$ för $\mathrm{col}(A)$, där $r=\mathrm{rang}(A)$. Eftersom egenrum som hör till olika egenvärden är linjärt oberoende, så kommer unionen av dessa två baser,

     $\mathcal{B}=\mathcal{B}_0\cup\mathcal{B}_1=\{u_1,\ldots,u_s,v_1,\ldots,v_r\}$

att vara en linjärt obereoende mängd. Samtidigt säger dimensionssatsen att $|\mathcal{B}|=s+r=n$. Från detta drar vi slutsatsen att $\mathcal{B}$ är en bas av egenvektorer för $\mathbb{R}^n$.

Om vi nu uttrycker $A$ i vår bas $\mathcal{B}$, så får vi följande matris:

och vi drar slutsatsen att

     $\mathrm{tr}(A)=0+\cdots+0+1+\cdots+1=r=\mathrm{rang}(A)\,.\qquad\qquad\square$

Kommentar 1. Från resonemanget ovan kan vi dra slutsatsen att alla engångsmatriser, upp till lämpligt basbyte, har samma enkla form som den projektionsmatris $P$ vi såg i trådstarten. Ett mer vedertaget namn för "engångsmatriser" är faktiskt just projektionsmatriser. Ännu vanligare är benämningen idempotenta matriser, som redan har dykt upp ett par gånger i tråden.

Kommentar 2. Vill man göra beviset mer elementärt genom att undvika användningen av egenvärden/egenvektorer (men då samtidigt göra bevisstrategin mindre intuitiv), så kan man direkt (baserat på inspiration från ovan?) välja baser $\mathcal{B}_0=\{u_1,\ldots,u_s\}$ och $\mathcal{B}_1=\{v_1,\ldots,v_r\}$ för $\mathrm{null}(A)$ respektive $\mathrm{col}(A)$. Enligt dimensionssatsen kommer unionen $\mathcal{B}=\mathcal{B}_0\cup\mathcal{B}_1$ då att ha maximalt $n$ stycken element. Samtidigt spänner $\mathcal{B}$ upp hela $\mathbb{R}^n$, eftersom varje $v\in\mathbb{R}^n$ kan skrivas som $v=(v-Av)+Av$, där $Av\in\mathrm{col}(A)$ och det faktum att $A$ är en engångsmatris ger att $v-Av\in\mathrm{null}(A)$. Vi drar därför slutsatsen att $\mathcal{B}$ är en bas för $\mathbb{R}^n$, och fortsätter sedan som ovan.

Väldigt trevligt bevis!

SeriousCephalopod skrev:

Kruxet ligger som sagt i att vi endast vet att geometriska multpliciteten är mindre än den algebraiska men inte, utifrån texten, att de är lika.

Mja, om A är idempotent är dimensionen av värderummet V(A) (dvs rang(A)) är lika med antalet linjärt oberoende egenvektorer med egenvärdet 1. Det innebär att den algebraiska- och geometriska multipliciteten för egenvärdet 1 sammanfaller (och är lika med rang(A)).

Eftersom dimensionssatsen garanterar att dimensionen av N(A) är $n-dim\, V(A)$  och multipliciteten av egenvärdet 0 är just $n-dim\, V(A)$ kan vi dra slutsatsen att de två egenrummen tillsammans kan uppbåda  n linjärt oberoende egenvektorer (varje bas till N(A) uppfyller ju $A\mathbf{e}_i=0\mathbf{e}_i$). Den idempotenta matrisen A är alltså diagonaliserbar. Ett annat sätt att formulera det är att varje egenvärdes geometriska multiplicitet är lika med dess algebraiska.

I det exempel tar du upp är A en matris där dimensionen av värderummet är 3, men där den algebraiska multipliciteten till egenvärdet 1 begränsar antalet egenvektorer till 2. Egenvektorerna till egenvärdet 1 kan inte utgöra en bas för V(A). Dessutom råder ett underskott på dimensioner (det finns bara en kvar till N(A) enligt dimensionssatsen). Vi måste alltså ge upp våra tappra försök att diagonalisera A. De två egenrummen har helt enkelt inte tillräckligt många linjärt oberoende egenvektorer.

Ett annat sätt att formulera det är att för egenvärdet 0 blev den geometriska multipliciteten strikt mindre än den algebraiska, and thats a big no-no.

Ett annat kort bevis är att hänvisa till Jordans normalform. Är matrisen skriven på Jordanform (efter ett basbyte som ju inte ändrar rang/spår) så är det uppenbart att ett Jordanblock uppfyller J^2=J omm det är en diagonalmatris med enbart ettor eller nollor. Då varje Jordanblock är diagonalt så är matrisen diagonal och vi är klara.

Annars så är ett trevligt sätt att titta på V som en direkt summa av nollrum och värderum, genom att vi sätter v=Av+(v-Av) (som varit uppe som förslag på approach tidigare).

Uppenbart så ligger Av i värderummet (där A agerar som identitet) och v-Av i nollrummet så vi skriver varje vektor som en summa av en vektor från nollrum och värderum på unikt sätt (det är trivialt att skärningen är nollvektorn). Välj en bas för vardera vektorrummen och vi är klara (igen genom att matrisen är diagonal).

JohanB skrev:

Ett annat kort bevis är att hänvisa till Jordans normalform. Är matrisen skriven på Jordanform (efter ett basbyte som ju inte ändrar rang/spår) så är det uppenbart att ett Jordanblock uppfyller J^2=J omm det är en diagonalmatris med enbart ettor eller nollor. Då varje Jordanblock är diagonalt så är matrisen diagonal och vi är klara.

Ohh, snyggt! Jag hade helt räknat bort JCF som verktyg eftersom det kräver att vi jobbar över en algebraiskt sluten kropp, och det här problemet handlar om reella matriser. Men en stunds funderande ger att detta inte är någon fara, eftersom vi enkelt kan översätta från $\mathbb{R}^n$ till $\mathbb{C}^n$ genom att komplexifiera!

Mer precist så kan vi till varje reellt vektorrum $V$ associera ett komplext vektorrum $V^\mathbb{C}$ där vektorerna består av formella summor $u+iv$, där $u,v\in V$. Man kan visa att varje $\mathbb{R}$-bas för $V$ är en $\mathbb{C}$-bas för $V^\mathbb{C}$, så $\dim_\mathbb{R}(V)=\dim_\mathbb{C}(V^\mathbb{C})$.

Vidare kan vi till varje operator $T\colon V\to V$ associera en komplexifierad operator $T^\mathbb{C}\colon V^\mathbb{C}\to V^\mathbb{C}$ definerad genom $T^\mathbb{C}(u+iv)=T(u)+iT(v)$. Det är enkelt att visa att för varje val av bas för $V$ och $V^\mathbb{C}$ så kommer $T$ och $T^\mathbb{C}$ att ha samma matrisrepresentation. Från detta följer att $T$ och $T^\mathbb{C}$ har samma spår. Vidare kan man också visa att $\mathrm{range}(T^\mathbb{C})=\mathrm{range}(T)^\mathbb{C}$, vilket innebär att

  $\mathrm{rank}(T^\mathbb{C})=\dim_\mathbb{C}(\mathrm{range}(T^\mathbb{C}))=\dim_\mathbb{C}(\mathrm{range}(T)^\mathbb{C})=\dim_\mathbb{R}(\mathrm{range}(T))=\mathrm{rank}(T)\,,$

dvs. även rangen förblir oförändrad om man komplexifierar. 

Det är därför helt lugnt att omtolka en matris $A\in\mathbb{R}^{n\times n}$ som en matris $A\in\mathbb{C}^{n\times n}$ när man vill undersöka rang och spår. Ett användbart faktum som jag har aldrig reflekterat över förrut! :D