Rekursionsekvationer

"Bestäm explicit form till $e_{n} = e_{n - 1} - 2, e_{1} = 0$ ."

Jag får fram rätt svar m.h.a. backtracking men inte med användning av karakteristiska ekvationen.

/🐎

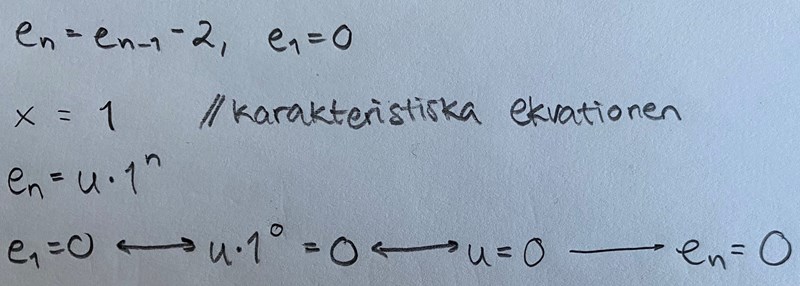
Nja Du ska väl ha

$u\cdot 1^1=0$ ? Men det förändrar väl inget

Ja, såklart, @dr_lund. Tack för noteringen. Som du säger, det förändrar dock inte att jag får fram en ekvation vilket jag tycker jag ändå bör få. Genom backtracking får jag fram en.

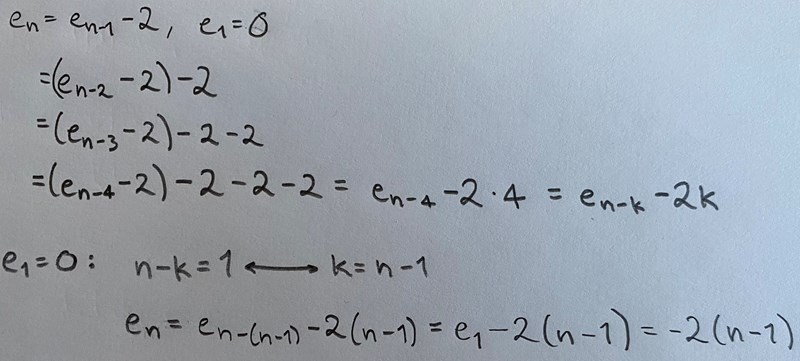
Jag får det inte till att stämma...

Det hade lett till olika ekvationer för varje $e$ .

Varför krångla till det?

e_n=e_n-1-2, e₁=0

e₂=0-2=-2

e₃=-2-2=-4

e₄=-4-2=-6

Rita upp eller "se det i huvudet". Du får en rät linje e=-2n+2 eller e=-2(n-1) om du föredrar det.

Om meningen med uppgiften är att lära sig metoden, förstår jag anledningen till krånglet.

Ett försök till metodisk lösning (jfr lösning av inhomogen diff.ekv.)

Svara

Visa senaste svar