Riktig klurig uppgift kring lutande plan
Hej, har stött på följande uppgift och är lite osäker på om jag tänker rätt.
Jag tänker att jag ritar ut kraftdiagram på båda objekten och använder Newtons andra lag för att hitta uttryck för accelerationen. Eftersom båda objekten har samma acceleration sätter jag dessa uttryck lika med varandra och löser ut för spännkraften. Tänker jag rätt?
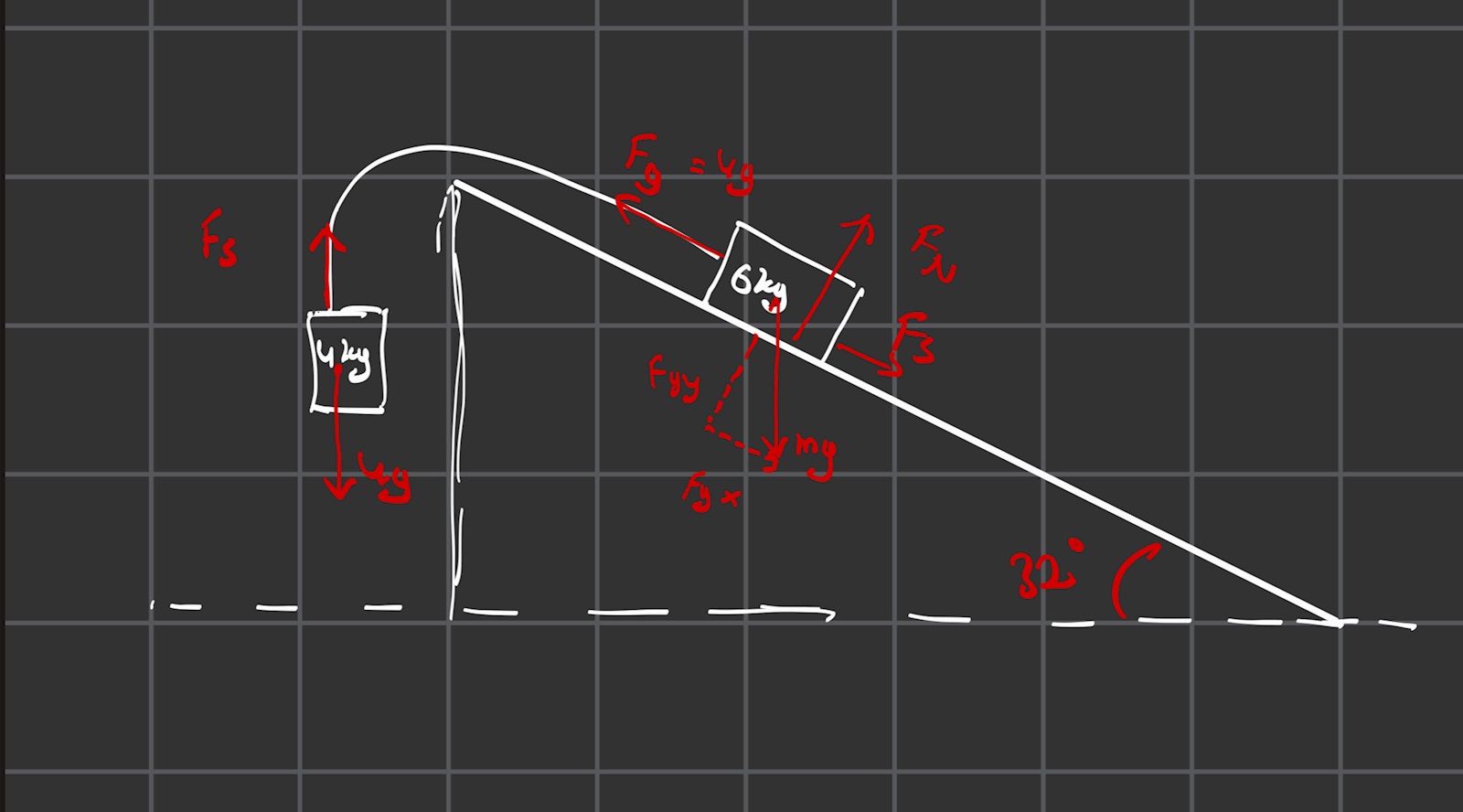Stämmer detta?
Nej, det stämmer inte att massan på det lutande planet dras av en kraft i repet. Snörkraften är lika stor i båda ändarna, dvs. massan på planet dras bakåt av en kraft , precis som den mindre massan som hänger.
Men din plan om att sätta accelerationerna lika är bra!
Okej, men varför är det inte så? Den ena vikten drar ju ned med sin egen tyngd? I en del liknande uppgifter har jag resonerat så och det har blivit rätt. Kanske är annorlunda om man har två föremål varav det ena ligger på ett lutande plan?
Men hur ska kraftsituationen se ut?
Nej, den hängande vikten drar inte i vikten på det lutande planet, repet drar i den! Det är alltså snörkraften som drar den på planet belägna massan mot den hängande massan. Så här tänker jag mig friläggningen:
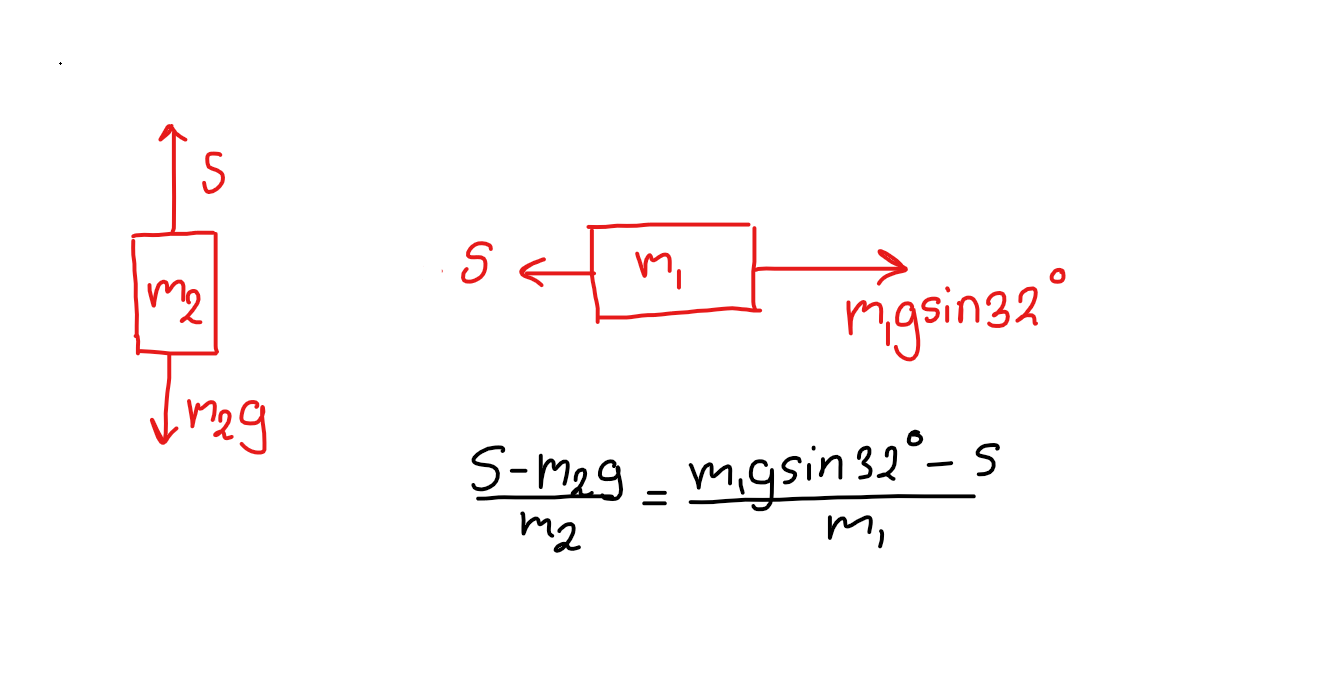
Ok. Men ska man inte dividera med den totala massan i båda fallen?
I den första ekvationen, här nedan, betraktas hela systemet. I den andra betraktas enbart m2
m2•g - m1•g•sin(α) = (m1 + m2)•a
m2•g - S = m2•a
S = 4(g -a) =
= 4g - 4•[(4g - 6g•sin(32))/10] =
= 4g - 4(4 - 3,18)g/10 ≈
≈ 40 - 4•0,82 ≈ 37 N
Du kan alltså strunta i systemets interna krafter
naytte skrev:Du kan alltså strunta i systemets interna krafter
Fast det är vad den här uppgiften frågar efter: bestäm spännkraften i tråden.
Jag menade om han ville ha systemets acceleration. Eftersom han har massan på t.ex m2 blir det sedan enkelt att räkna fram spännkraften S med Newton II.
Han kan alltså antingen lösa ekvationen i bilden jag gjorde, eller räkna fram accelerationen på hela systemet först och sedan räkna fram spännkraften.
