"Se gränsvärdet som derivata i x=1 till en funktion f(x)."
Uppgiften lyder:
"Betrakta:
Se gränsvärdet som derivata i x=1 till en funktion f(x).
Bestäm funktionen f′(x) och beräkna gränsvärdet."
Jag förstår inte vad som menas med "se gränsvärdet som derivata i x=1", eller jo det tror jag jag förstår, men när jag deriverar uttrycket i gränsvärdet ger det mig ej rätt svar. Jag får f'(x)=
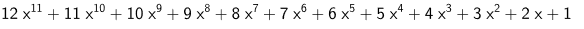
som inte stämmer...
Har jag missat något här?
Antingen använder du formeln för geometrisk summa baklänges eller så inser vi att di har , dvs derivatan i punkten x=1.
Skriv upp definitionen för (höger-)derivatan av funktionen f(x) i punkten där x= 0. Jämför det med ditt gränsvärde. Vilken funktion handlar det om?
Smaragdalena skrev:Skriv upp definitionen för (höger-)derivatan av funktionen f(x) i punkten där x= 0. Jämför det med ditt gränsvärde. Vilken funktion handlar det om?
Grymt!
Tack för hjälpen!



