Skriva om gränser i sfäriska koordinater
Halloj!
Jag sitter med trippelintegralen nedan:
där
Jag förstår att området man ska integrera över är snittet av en kon och en sfär. För åskådlighetens skull framgår en bild nedan på området:
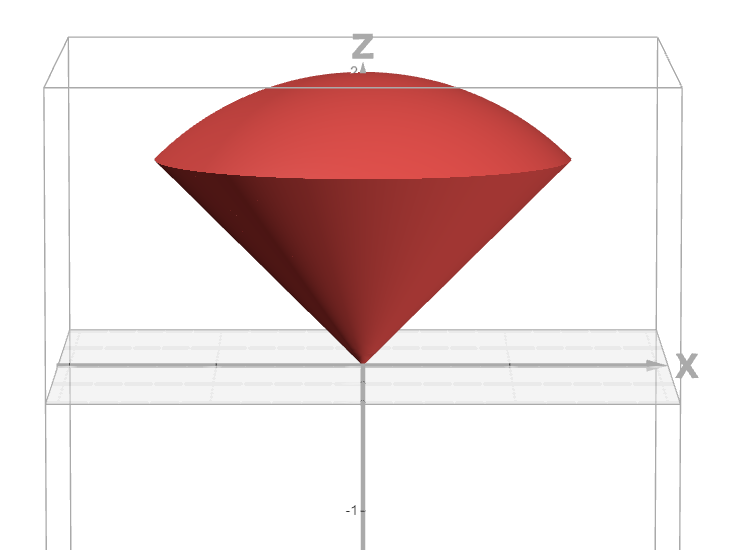 Jag vill byta till sfäriska koordinater för att beräkna detta. Jag vet att och jag tänker att , vinkeln mätt i -planet mot -axeln, måste löpa över .
Jag vill byta till sfäriska koordinater för att beräkna detta. Jag vet att och jag tänker att , vinkeln mätt i -planet mot -axeln, måste löpa över .
Däremot har jag betydligt större problem med att bestämma gränserna för och .
Hjälp skulle uppskattas!
Radien går väl från 0 till 2 och vinkeln från 0 till pi/4.
Hur kommer du fram till att går från till ?
Titta på tvärsnittet i x-z-planet. Det blir en cirkelsektor. Vinkeln mot z-axeln är pi/4.
Tillägg: 25 maj 2025 15:05

Jag hänger fortfarande inte riktigt med på hur du kommer fram till att den är just . Vilka mått i figuren använde du för att komma fram till det?
Använder man följande form av sfäriska koordinater:
så betyder de sfäriska koordinaterna följande:
- avståndet till origo
- vinkeln i -planet, mätt från positiva -axeln
- vinkeln mätt från positiva -axeln
Hela rummet fås när , , och . Funktionaldeterminanten är då . (OBS: i ursprungliga inlägget är fel)
I den givna kroppen ska . Tittar man på snittet med xz-planet som PATENTERAMERA föreslagit, så är och därmed i detta plan. Linjerna har 45-graders lutning, så vinkeln till -axeln kan som störst bli .
Man kan också hitta gränserna algebraiskt genom att sätta in uttrycken för , och i kroppens olikheter:
- blir och därmed
- blir , vilket förenklas till eftersom man redan vet att ligger inom . Olikheten löses därmed av
Okej, tack!
Men hur vet vi genom lösning av olikheten att ? Det finns väl två delintervall till sådana att satisfieras. Vad händer med det andra?
Vilket är det andra intervallet?
Det var inget.
Insåg precis att kosinus ju blir negativ efter .
Nevermind! :D
Jag undrar också en sak om genomlöpningen för . Visst är det samma sak att skriva dess genomlöpning som ?
Jag tänker att när vi väl beräknar integralen så får vi helt enkelt
naytte skrev:Jag undrar också en sak om genomlöpningen för . Visst är det samma sak att skriva dess genomlöpning som ?
...
Ja, exakt. Intervallet för ska täcka ett helt varv. Det spelar ingen roll om det är från -pi till pi, eller från 0 till 2pi (eller från pi/4 till 9pi/4).
Man kan gärna vara flexibel med det exakta valet av intervallet. Fördelen med intervallet från -pi till pi är att man kan utnyttja symmetrier hos jämna respektive udda funktioner.
Okej, så vi har alltså våra gränser:
Kan vi ställa upp de nästlade integralerna i vilken ordning vi vill nu eller finns det något man behöver tänka på där? I vissa nästlade integraler får man ju olika svar beroende på i vilken ordning man integrerar.
naytte skrev:Okej, så vi har alltså våra gränser:
Kan vi ställa upp de nästlade integralerna i vilken ordning vi vill nu eller finns det något man behöver tänka på där? I vissa nästlade integraler får man ju olika svar beroende på i vilken ordning man integrerar.
Kompakt område, ingen generaliserad integral, inga singulariteter. Skall inte vara några problem.



