Substitution, primitiv funktion
Hej!
kan någon vara så snäll och hjälpa mig med denna uppgift? Den lyder:
bestäm, med hjälp av lämplig substitution, en primitiv funktion till:
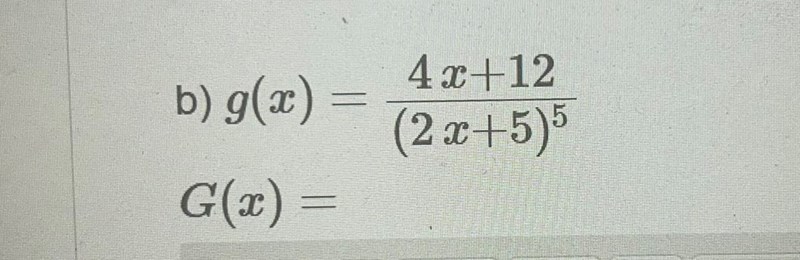
jag tänker spontant på:
∫f(X)dx = ∫f(g(t))g’(t)dt där X = g(t)
och tänker:
t= 2x + 5
g(t) = 2t
g’(t) = 1/2 dt
∫(4x+12)/(1/2 * t^5)dt = ∫(4x+12) * 2/t^5 = 2 ∫(4x+12)/t^5 = 8∫(x+3)/t^5 = (derivera) = 8 * 1/ (t^6/6) = 48/(2x +5) + C
men detta är fel… hur gör jag tro?
mvh!
Substitutionen tycker jag var lämplig; du bör dock även utföra substitutionen i täljaren.
När du substituerar ska det aldrig stå både x och t i integranden. Du sätter t=2x+5. Det ger x=(t-5)/2 som ger dx =1/2 dt som du också kommit fram till. Integrandens täljare 4x+12=4(t-5)/2+12=2t-10+12=2t+2 och nämnaren t5 du skrivit.
Tomten skrev:När du substituerar ska det aldrig stå både x och t i integranden. Du sätter t=2x+5. Det ger x=(t-5)/2 som ger dx =1/2 dt som du också kommit fram till. Integrandens täljare 4x+12=4(t-5)/2+12=2t-10+12=2t+2 och nämnaren t5 du skrivit.
okej, tack! Nu har jag finjusterat lite, men det blir ändå fel. Detta är min "lösning":
dvs svaret är: -1/3(2x+5)^3 - 1/5(2x+5)^5 + C, men det är tyvärr fel, vart har det gått snett?
Du tycks ha fått -5 i ena nämnaren då du borde fått -4.
Bedinsis skrev:Du tycks ha fått -5 i ena nämnaren då du borde fått -4.
Jag förstår! Tack :)

