Svår dubbelintegral

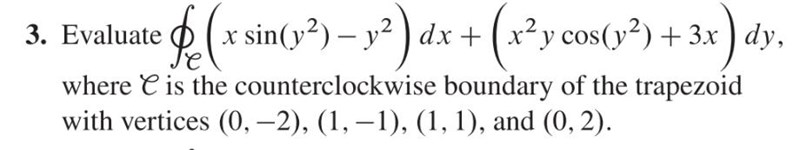
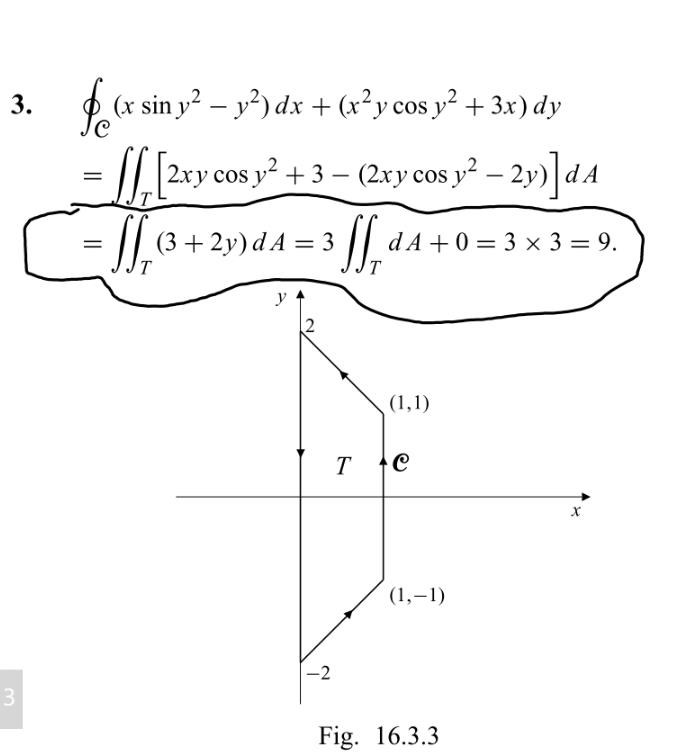
De använder Greens formel (det borde de ha nämnt).

Jo det förstår jag. Men undrar om det dom gör efter det dvs från

 ${\iint }_T(3+2y)dA$

till

$3{\iint }_{T}dA+0$

På samma sätt gör dom här. Vad menar dom tillexempel att $\frac{}{x}$

I det här fallet så är R en boll

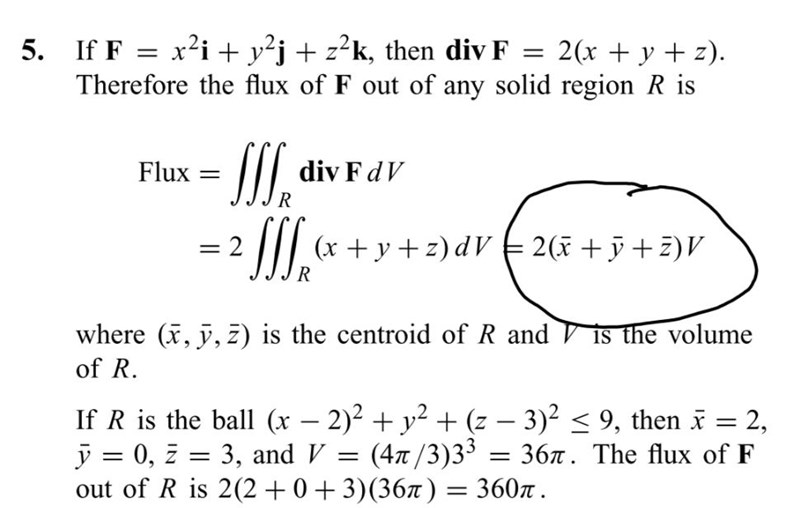
Ditt område är symmetriskt med avseende på y, och 2y är en udda funktion, så den delen av integralen har värdet 0. Bollen är också symmetrisk.

I fallet med integralen:

$2\displaystyle\iiint_R x+y+z\ dV$

utnyttjar man det faktum att integralen av en linjär funktion (egentligen kanske man skall säga affin funktion på universitetsnivå) på ett området kan beräknas genom att multiplicera integrandens medelvärde med områdets storlek.

Det är samma regel som gör att man kan beräkna sträckan genom att multiplicera tiden med medelhastigheten $\bar{v}$ ifall hastigheten är en linjär funktion.

Hej!

Först skriver de

    $\displaystyle\iint_{T}(3+2y)\,dA = \iint_{T}3\,dA+\iint_{T}2y\,dA.$

Sedan beräknar de dubbelintegralerna var för sig. 

    $\displaystyle\iint_{T}3\,dA = 3\iint_{T}\,dA = 3\cdot \text{Area}(A) = 3 \cdot \frac{(2+4)1}{2} = 9$

där man använder formeln för parallelltrapets area. Den andra dubbelintegralen beräknas

    $\displaystyle\iint_{T}2y\,dA = 2\iint_{T}y\,dxdy = 2\int_{x=0}^{1}\{\int_{y=-a(x)}^{a(x)}y\,dy\}\,dx$

där punkten $a(x)$ ligger på den sneda sidan av parallelltrapetset. 

Den inre enkelintegralen med avseende på $y$ är

    $\displaystyle\int_{-a(x)}^{a(x)}y\,dy = [\frac{y^2}{2}]_{-a(x)}^{a(x)} = \frac{1}{2}(a(x)^2-(-a(x))^2) = 0$

eftersom det gäller att $(-1)^2 = 1$.