Tanke om matematik (och att lösa ekavtioner av olika slag)
Hej!
Kort version: Jag är förvirrad över var min förmåga att lösa en ekvation algebraiskt (="för hand") slutar när det kommer till trigonometriska (matte4) och diff ekvationer (matte5).
Lång version: Jag har märkt av en sak. Ända sen matte 1 (eller kanske så långt jag kan minnas faktiskt) har vi i skolan lärt oss om att lösa ekvationer. Mer och mer komplicerade sådana, och som hjälp på vägen även fått med regler/formler, det kändes tryggt och inget fanns utom räckhåll (eller jo, men jag visste exakt vad som var utom räckhåll och vi höll oss (som klass, med läraren i spetsen) borta från det). Tex vid matte 2, pq-formeln funkade på allt, och ifall vi stötte på en (då) ovanlig tredjegradare visste vi att där har vi ingen formel (som vi hade lärt oss), så då gällde miniräknare. Det var tydligt var våra begränsningar gick liksom, och vad vi skulle göra när vi såg x (pun intended!).
Men i matte 4 hände något, när vi lärde oss mer om trigonometriska funktioner och ekvationer. Då fanns ingen klassifikation på ekvationerna och det var osäkert vid åsynen av en sådan, om jag ens kunde lösa den. Det var inte alls lika lätt att veta vilka jag kunde/inte kunde läsa. Oftast fanns dock miniräknaren, men det har jag länge ansett vara mindre elegant än att lösa algebraiskt så min första tanke var aldrig att plocka upp den.
Diff ekvationerna i matte5 ska vi inte ens tala om. Jag läste precis på wikipedia att det inte ens finns lösningar på vissa, även om man hade dator/miniräknare. Jag blir förvirrad över vad jag kan och inte kan. Det känns som att jag är i djupt vatten, ingen kontroll. Är detta en bieffekt av att klättra i matten?
Qetsiyah skrev:Hej!
Kort version: Jag är förvirrad över var min förmåga att lösa en ekvation algebraiskt (="för hand") slutar när det kommer till trigonometriska (matte4) och diff ekvationer (matte5).
Lång version: Jag har märkt av en sak. Ända sen matte 1 (eller kanske så långt jag kan minnas faktiskt) har vi i skolan lärt oss om att lösa ekvationer. Mer och mer komplicerade sådana, och som hjälp på vägen även fått med regler/formler, det kändes tryggt och inget fanns utom räckhåll (eller jo, men jag visste exakt vad som var utom räckhåll och vi höll oss (som klass, med läraren i spetsen) borta från det). Tex vid matte 2, pq-formeln funkade på allt, och ifall vi stötte på en (då) ovanlig tredjegradare visste vi att där har vi ingen formel (som vi hade lärt oss), så då gällde miniräknare. Det var tydligt var våra begränsningar gick liksom, och vad vi skulle göra när vi såg x (pun intended!).
Men i matte 4 hände något, när vi lärde oss mer om trigonometriska funktioner och ekvationer. Då fanns ingen klassifikation på ekvationerna och det var osäkert vid åsynen av en sådan, om jag ens kunde lösa den. Det var inte alls lika lätt att veta vilka jag kunde/inte kunde läsa. Oftast fanns dock miniräknaren, men det har jag länge ansett vara mindre elegant än att lösa algebraiskt så min första tanke var aldrig att plocka upp den.
Diff ekvationerna i matte5 ska vi inte ens tala om. Jag läste precis på wikipedia att det inte ens finns lösningar på vissa, även om man hade dator/miniräknare. Jag blir förvirrad över vad jag kan och inte kan. Det känns som att jag är i djupt vatten, ingen kontroll. Är detta en bieffekt av att klättra i matten?
Alltså, för mig så blir det så när jag bara "accepterar" olika formler och regler. Därför så gör jag aldrig det längre, jag tar min tid och försöker bryta ner varenda matematiskt påstående och verkligen se till att förstå vad det är som händer.
Ta din tid och gå igenom allt som du inte har stenkoll på. Kom också ihåg att många saker kan man helt enkelt inte förstå än. Jag som bara har läst gymnasiekurser kan inte förstå varför man får ut sträckan om man tar arean under en graf. (integrerar en graf) Många har sagt att jag måste gå universitetsmatte för att få en bättre förståelse. Gör så gott du kan bara om du måste klara av prov och sånt men annars så tycker jag att du ska låta det ta den tiden det tar för att fullständigt förstå vad det är du håller på med.
Korra skrev:
Jag som bara har läst gymnasiekurser kan inte förstå varför man får ut sträckan om man tar arean under en graf. (integrerar en graf) Många har sagt att jag måste gå universitetsmatte för att få en bättre förståelse.
Lite OT men: Varför? Du har ju läst upp till åtminstone matematik 4, då har du ju gått igenom derivata och integraler.
I övrigt skulle jag tro att du har rätt. Att bara lära sig använda formler kommer inte fungera i längden i varken fysik eller matematik. Det är viktigt att man förstår varför man ska använda X formel istället för Y. Det kommer bara från förståelse.
woozah skrev:Korra skrev:
Jag som bara har läst gymnasiekurser kan inte förstå varför man får ut sträckan om man tar arean under en graf. (integrerar en graf) Många har sagt att jag måste gå universitetsmatte för att få en bättre förståelse.
Lite OT men: Varför? Du har ju läst upp till åtminstone matematik 4, då har du ju gått igenom derivata och integraler.
gått igenom hur man löser dem osv. Men ingen, absolut ingen lärare har lyckats förklara för mig varför och hur det går till. Jag ställde frågan här också och jag fick inte heller så bra respons. Till slut så slutade jag att fråga och jag väntar tills jag är klar med några universitetskurser. Sedan får vi se om jag kan lyckas förstå hur det fungerar.
EDIT: Man studerar inte integraler och sånt på en sådan analytisk nivå på ma3/4.
Inga härledningar.
Korra skrev:Qetsiyah skrev:Hej!
Kort version: Jag är förvirrad över var min förmåga att lösa en ekvation algebraiskt (="för hand") slutar när det kommer till trigonometriska (matte4) och diff ekvationer (matte5).
Lång version: Jag har märkt av en sak. Ända sen matte 1 (eller kanske så långt jag kan minnas faktiskt) har vi i skolan lärt oss om att lösa ekvationer. Mer och mer komplicerade sådana, och som hjälp på vägen även fått med regler/formler, det kändes tryggt och inget fanns utom räckhåll (eller jo, men jag visste exakt vad som var utom räckhåll och vi höll oss (som klass, med läraren i spetsen) borta från det). Tex vid matte 2, pq-formeln funkade på allt, och ifall vi stötte på en (då) ovanlig tredjegradare visste vi att där har vi ingen formel (som vi hade lärt oss), så då gällde miniräknare. Det var tydligt var våra begränsningar gick liksom, och vad vi skulle göra när vi såg x (pun intended!).
Men i matte 4 hände något, när vi lärde oss mer om trigonometriska funktioner och ekvationer. Då fanns ingen klassifikation på ekvationerna och det var osäkert vid åsynen av en sådan, om jag ens kunde lösa den. Det var inte alls lika lätt att veta vilka jag kunde/inte kunde läsa. Oftast fanns dock miniräknaren, men det har jag länge ansett vara mindre elegant än att lösa algebraiskt så min första tanke var aldrig att plocka upp den.
Diff ekvationerna i matte5 ska vi inte ens tala om. Jag läste precis på wikipedia att det inte ens finns lösningar på vissa, även om man hade dator/miniräknare. Jag blir förvirrad över vad jag kan och inte kan. Det känns som att jag är i djupt vatten, ingen kontroll. Är detta en bieffekt av att klättra i matten?
Alltså, för mig så blir det så när jag bara "accepterar" olika formler och regler. Därför så gör jag aldrig det längre, jag tar min tid och försöker bryta ner varenda matematiskt påstående och verkligen se till att förstå vad det är som händer.
Ta din tid och gå igenom allt som du inte har stenkoll på. Kom också ihåg att många saker kan man helt enkelt inte förstå än. Jag som bara har läst gymnasiekurser kan inte förstå varför man får ut sträckan om man tar arean under en graf. (integrerar en graf) Många har sagt att jag måste gå universitetsmatte för att få en bättre förståelse. Gör så gott du kan bara om du måste klara av prov och sånt men annars så tycker jag att du ska låta det ta den tiden det tar för att fullständigt förstå vad det är du håller på med.
Vad menar du med att få ut en sträcka genom att hitta arean under en graf? Om du menar för hastighet/tid grafer så behövs definitivt inte någon universitetsmatte.
Om du menar denna så behöver du bara ha i åtanke att man inte beräknar en integral av funktionen som du vill veta längden av.
Jag tror förresten att du missförstod mitt problem, jag har inga problem med att lösa ekavtioner (som jag kan, enligt vad jag har lärt mig hittills upp till matte5) både snabbt och elegant. Problemet är att gränsen mellan vilka jag kan/inte kan lösa känns suddig.
Qetsiyah skrev:Vad menar du med att få ut en sträcka genom att hitta arean under en graf?
Denna grafen visar hur en hastighet för en cykel förändras. F(x) = hastighet x = t i sekunder
Om man deriverar denna funktionen så får man fram att F(x) = Accelerationen per x enhet (sekunder fortfarande)
Om jag skulle vilja veta hur långt cykeln har åkt efter 4 sekunder så beräknar man följande integral
Den primitiva funktionen för F(x) kallar vi G(x)
Hur kommer det sig att ger oss sträckan för funktionen i intervallet ??? Totalt obegripligt.
Korra skrev:Qetsiyah skrev:Hej!
Kort version: Jag är förvirrad över var min förmåga att lösa en ekvation algebraiskt (="för hand") slutar när det kommer till trigonometriska (matte4) och diff ekvationer (matte5).
Lång version: Jag har märkt av en sak. Ända sen matte 1 (eller kanske så långt jag kan minnas faktiskt) har vi i skolan lärt oss om att lösa ekvationer. Mer och mer komplicerade sådana, och som hjälp på vägen även fått med regler/formler, det kändes tryggt och inget fanns utom räckhåll (eller jo, men jag visste exakt vad som var utom räckhåll och vi höll oss (som klass, med läraren i spetsen) borta från det). Tex vid matte 2, pq-formeln funkade på allt, och ifall vi stötte på en (då) ovanlig tredjegradare visste vi att där har vi ingen formel (som vi hade lärt oss), så då gällde miniräknare. Det var tydligt var våra begränsningar gick liksom, och vad vi skulle göra när vi såg x (pun intended!).
Men i matte 4 hände något, när vi lärde oss mer om trigonometriska funktioner och ekvationer. Då fanns ingen klassifikation på ekvationerna och det var osäkert vid åsynen av en sådan, om jag ens kunde lösa den. Det var inte alls lika lätt att veta vilka jag kunde/inte kunde läsa. Oftast fanns dock miniräknaren, men det har jag länge ansett vara mindre elegant än att lösa algebraiskt så min första tanke var aldrig att plocka upp den.
Diff ekvationerna i matte5 ska vi inte ens tala om. Jag läste precis på wikipedia att det inte ens finns lösningar på vissa, även om man hade dator/miniräknare. Jag blir förvirrad över vad jag kan och inte kan. Det känns som att jag är i djupt vatten, ingen kontroll. Är detta en bieffekt av att klättra i matten?
Alltså, för mig så blir det så när jag bara "accepterar" olika formler och regler. Därför så gör jag aldrig det längre, jag tar min tid och försöker bryta ner varenda matematiskt påstående och verkligen se till att förstå vad det är som händer.
Ta din tid och gå igenom allt som du inte har stenkoll på. Kom också ihåg att många saker kan man helt enkelt inte förstå än. Jag som bara har läst gymnasiekurser kan inte förstå varför man får ut sträckan om man tar arean under en graf. (integrerar en graf) Många har sagt att jag måste gå universitetsmatte för att få en bättre förståelse. Gör så gott du kan bara om du måste klara av prov och sånt men annars så tycker jag att du ska låta det ta den tiden det tar för att fullständigt förstå vad det är du håller på med.
Snabbkurs om sträcka som area under en graf
Du vet att:
Om vi tar en kort tid och kallar den för så kallar vi den korta sträckan vi färdas som
i ett v-t-diagram ser det ut så här
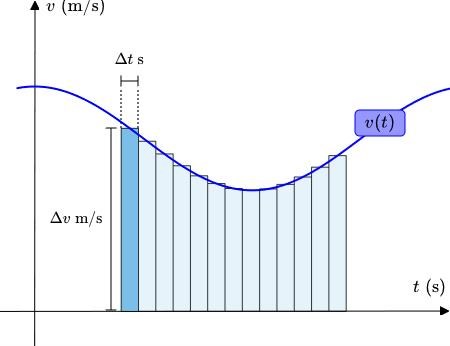 En kort tid färdas vi den korta sträckan och beräknar den i grafen som
En kort tid färdas vi den korta sträckan och beräknar den i grafen som
Du ser nu att är den lite mörkare blåa ytan i v-t-diagrammet.
Du vill nu summera alla ytor till höger om den lite mörkare blå:
När vi sedan gör extremt liten kallar vi den i stället ,
byter mot (bägge tecknen betyder en slags summa)
och blir lika med
Vi får då:
Korra skrev:Qetsiyah skrev:Vad menar du med att få ut en sträcka genom att hitta arean under en graf?
Denna grafen visar hur en hastighet för en cykel förändras. F(x) = hastighet x = t i sekunder
Om man deriverar denna funktionen så får man fram att F(x) = Accelerationen per x enhet (sekunder fortfarande)
Om jag skulle vilja veta hur långt cykeln har åkt efter 4 sekunder så beräknar man följande integral
Den primitiva funktionen för F(x) kallar vi G(x)
Hur kommer det sig att ger oss sträckan för funktionen ??? Totalt obegripligt.
Oj, det där borde du förstå! Kan ingen lärare förklara det där?
För det första ska du veta vad funktionen G anger, den anger hur långt cykeln har cyklat vid en tid t. Detta eftersom originalfunktionen F (det är vanligare med lilla f!) angav hastigheten vid en tid t. Om du deriverar G får du F, det hoppas jag du förstår varför. Följaktligen ska du få G om du integrerar F. Det är på grund av denna relation mellan F och G som du kan bestämma den definitiva integralen mellan 0 och 4 och på så sätt få reda på hur långt cykeln har cyklat mellan t=0 och t=4
Du missförstår. G(4)-G(0) ger oss inte sträckan för funktionen F(x), det är en matematisk felaktig mening. Den betyder ingenting. Det du menar är "hur kommer det sig att G(4)-G(0) anger hur långt en cykel (vars hastighet bestäms av F) har cyklat under mellan t=0 och t=4"?.
Affe Jkpg skrev:Snabbkurs om sträcka som area under en graf
Du vet att:
Om vi tar en kort tid och kallar den för så kallar vi den korta sträckan vi färdas som
i ett v-t-diagram ser det ut så här
En kort tid färdas vi den korta sträckan och beräknar den i grafen som
Du ser nu att är den lite mörkare blåa ytan i v-t-diagrammet.Du vill nu summera alla ytor till höger om den lite mörkare blå:
När vi sedan gör extremt liten kallar vi den i stället ,
byter mot (bägge tecknen betyder en slags summa)
och blir lika medVi får då:
Jag är fullt medveten om hur uträkningen går till, jag vet att dt betyder ett pytte intervall i x ledet.
Men det är inte det jag frågar efter. :)
Hur kommer det sig att arean under grafen blir till sträckan? Varför just sträckan?
fine. Om du menar att jag bara ska "förstå" att det är så bara för det stämmer algebraiskt så kommer jag bara att lära mig formeln liksom. Inte förstå att det verkligen är så, hur ska man föreställa sig det? Sträcka = förändring i sträcka multiplicerat med tiden?
En sak till, Ja du får följande likhet Men hur kommer det sig att den primitiva funktionen till v(t) ger arean under v(t) ? :)
Qetsiyah skrev:Korra skrev:Qetsiyah skrev:Vad menar du med att få ut en sträcka genom att hitta arean under en graf?
Denna grafen visar hur en hastighet för en cykel förändras. F(x) = hastighet x = t i sekunder
Om man deriverar denna funktionen så får man fram att F(x) = Accelerationen per x enhet (sekunder fortfarande)
Om jag skulle vilja veta hur långt cykeln har åkt efter 4 sekunder så beräknar man följande integral
Den primitiva funktionen för F(x) kallar vi G(x)
Hur kommer det sig att ger oss sträckan för funktionen ??? Totalt obegripligt.Oj, det där borde du förstå! Kan ingen lärare förklara det där?
För det första ska du veta vad funktionen G anger, den anger hur långt cykeln har cyklat vid en tid t. Detta eftersom originalfunktionen F (det är vanligare med lilla f!) angav hastigheten vid en tid t. Om du deriverar G får du F, det hoppas jag du förstår varför. Följaktligen ska du få G om du integrerar F. Det är på grund av denna relation mellan F och G som du kan bestämma den definitiva integralen mellan 0 och 4 och på så sätt få reda på hur långt cykeln har cyklat mellan t=0 och t=4
Du missförstår. G(4)-G(0) ger oss inte sträckan för funktionen F(x), det är en matematisk felaktig mening. Den betyder ingenting. Det du menar är "hur kommer det sig att G(4)-G(0) anger hur långt en cykel (vars hastighet bestäms av F) har cyklat under mellan t=0 och t=4"?.
Jag vet att om man integrerar F(x) så får man G(x) och om man deriverar G(x) så får man F(x). Jag känner också till derivatans definition och jag vet hur jag kan härleda dessa integreringar och deriveringar. Jag förstår varför det blir som det blir.
Detta är fortfarande oklart, hur kommer det sig att ger oss arean under grafen F(x) ?
Korra skrev:Qetsiyah skrev:Korra skrev:Qetsiyah skrev:Vad menar du med att få ut en sträcka genom att hitta arean under en graf?
Denna grafen visar hur en hastighet för en cykel förändras. F(x) = hastighet x = t i sekunder
Om man deriverar denna funktionen så får man fram att F(x) = Accelerationen per x enhet (sekunder fortfarande)
Om jag skulle vilja veta hur långt cykeln har åkt efter 4 sekunder så beräknar man följande integral
Den primitiva funktionen för F(x) kallar vi G(x)
Hur kommer det sig att ger oss sträckan för funktionen ??? Totalt obegripligt.Oj, det där borde du förstå! Kan ingen lärare förklara det där?
För det första ska du veta vad funktionen G anger, den anger hur långt cykeln har cyklat vid en tid t. Detta eftersom originalfunktionen F (det är vanligare med lilla f!) angav hastigheten vid en tid t. Om du deriverar G får du F, det hoppas jag du förstår varför. Följaktligen ska du få G om du integrerar F. Det är på grund av denna relation mellan F och G som du kan bestämma den definitiva integralen mellan 0 och 4 och på så sätt få reda på hur långt cykeln har cyklat mellan t=0 och t=4
Du missförstår. G(4)-G(0) ger oss inte sträckan för funktionen F(x), det är en matematisk felaktig mening. Den betyder ingenting. Det du menar är "hur kommer det sig att G(4)-G(0) anger hur långt en cykel (vars hastighet bestäms av F) har cyklat under mellan t=0 och t=4"?.
Jag vet att om man integrerar F(x) så får man G(x) och om man deriverar G(x) så får man F(x). Jag känner också till derivatans definition och jag vet hur jag kan härleda dessa integreringar och deriveringar. Jag förstår varför det blir som det blir.
Detta är fortfarande oklart, hur kommer det sig att ger oss arean under grafen F(x) ?
Jaha... Det vet jag fan inte heller, det blir ett hopp där emellan minirektanglarna och integralen
Hej Qetsiyah!
Generellt är det ett tecken på att ens kunskap har vuxit när man istället för att få ett svar på en fråga får en ny fråga, fast på ett djupare plan.
Ett exempel: Om jag skulle be dig lösa ekvationen , vad skulle du göra då?
Qetsiyah skrev:Jaha... Det vet jag fan inte heller, det blir ett hopp där emellan minirektanglarna och integralen
Det är precis det jag har frågat efter så länge att det börjar göra ont i halsen. (på skoj förstås!)
Albiki skrev:Hej Qetsiyah!
Generellt är det ett tecken på att ens kunskap har vuxit när man istället för att få ett svar på en fråga får en ny fråga, fast på ett djupare plan.
Ett exempel: Om jag skulle be dig lösa ekvationen , vad skulle du göra då?
är det en kuggfråga? haha. Jag skulle lösa den på bokstavligen mindre än en sekund utan papper eller penna.
Korra skrev:Qetsiyah skrev:Jaha... Det vet jag fan inte heller, det blir ett hopp där emellan minirektanglarna och integralen
Det är precis det jag har frågat efter så länge att det börjar göra ont i halsen. (på skoj förstås!)
Det är däremot enkelt att förstå om vi talar om y=x (det blir trianglar då, prova själv)
Qetsiyah skrev:Albiki skrev:Hej Qetsiyah!
Generellt är det ett tecken på att ens kunskap har vuxit när man istället för att få ett svar på en fråga får en ny fråga, fast på ett djupare plan.
Ett exempel: Om jag skulle be dig lösa ekvationen , vad skulle du göra då?
är det en kuggfråga? haha. Jag skulle lösa den på bokstavligen mindre än en sekund utan papper eller penna.
Då visar du att du inte har förstått problemet. Vad handlar ekvationen om?
Albiki skrev:Qetsiyah skrev:Albiki skrev:Hej Qetsiyah!
Generellt är det ett tecken på att ens kunskap har vuxit när man istället för att få ett svar på en fråga får en ny fråga, fast på ett djupare plan.
Ett exempel: Om jag skulle be dig lösa ekvationen , vad skulle du göra då?
är det en kuggfråga? haha. Jag skulle lösa den på bokstavligen mindre än en sekund utan papper eller penna.
Då visar du att du inte har förstått problemet. Vad handlar ekvationen om?
Menar du typ, "Vad ska man multiplicera med 2 för att få 3?" (Förlåt, det är inte min tråd men jag är nyfiken :) )
Alla funktioner har inte en antiderivata. Men för dom som har det är det lätt att beräkna integralen över funktionen. Läs på om analysens fundamentalsats för mer insikter om det.
Albiki skrev:Qetsiyah skrev:Albiki skrev:Hej Qetsiyah!
Generellt är det ett tecken på att ens kunskap har vuxit när man istället för att få ett svar på en fråga får en ny fråga, fast på ett djupare plan.
Ett exempel: Om jag skulle be dig lösa ekvationen , vad skulle du göra då?
är det en kuggfråga? haha. Jag skulle lösa den på bokstavligen mindre än en sekund utan papper eller penna.
Då visar du att du inte har förstått problemet. Vad handlar ekvationen om?
Jag kan inte ge ett svar som tillför något nytt (tex en närmare förklaring om dess innebörd). Det kan bara bli en totalt intressant översättning mellan matte och svenska. 2x=3 är självförklarande.
Korra skrev:Albiki skrev:Qetsiyah skrev:Albiki skrev:Hej Qetsiyah!
Generellt är det ett tecken på att ens kunskap har vuxit när man istället för att få ett svar på en fråga får en ny fråga, fast på ett djupare plan.
Ett exempel: Om jag skulle be dig lösa ekvationen , vad skulle du göra då?
är det en kuggfråga? haha. Jag skulle lösa den på bokstavligen mindre än en sekund utan papper eller penna.
Då visar du att du inte har förstått problemet. Vad handlar ekvationen om?
Menar du typ, "Vad ska man multiplicera med 2 för att få 3?" (Förlåt, det är inte min tråd men jag är nyfiken :) )
Jag väntar på Qetsiyahs svar och bortser från ditt inlägg tillsvidare. Visar det sig att hen är ointresserad av att diskutera med mig så kan jag återkomma till din fråga.
Aerius skrev:Alla funktioner har inte en antiderivata. Men för dom som har det är det lätt att beräkna integralen över funktionen. Läs på om analysens fundamentalsats för mer insikter om det.
Oj där ser man. Jag trodde att alla funktioner hade en primitiv funktion, men icke sann icke
Qetsiyah skrev:Albiki skrev:Qetsiyah skrev:Albiki skrev:Hej Qetsiyah!
Generellt är det ett tecken på att ens kunskap har vuxit när man istället för att få ett svar på en fråga får en ny fråga, fast på ett djupare plan.
Ett exempel: Om jag skulle be dig lösa ekvationen , vad skulle du göra då?
är det en kuggfråga? haha. Jag skulle lösa den på bokstavligen mindre än en sekund utan papper eller penna.
Då visar du att du inte har förstått problemet. Vad handlar ekvationen om?
Jag kan inte ge ett svar som tillför något nytt (tex en närmare förklaring om dess innebörd). Det kan bara bli en totalt intressant översättning mellan matte och svenska. 2x=3 är självförklarande.
Nej, 2x=3 är inte självförklarande. Du gör en massa antaganden här, baserat på din bristande kunskap om matematik.
Ekvationen är bara meningsfull om man tydligt specificerar vad den innebär. Vad betecknar 2? Är det det reella talet 2? (Det behöver det inte vara.) Vad betecknar 2x? Är det multiplikation mellan det reella talet 2 och x? Är multiplikationen definierad? (Det beror på vad x är; om x betecknar reellt tal så är multiplikationen definierad. Men om x är en vektor och multiplikationen är vektoriell produkt så är multiplikationen 2x nonsens om 2 är ett reellt tal.) Vad betecknar likhetstecknet? Är det likhet mellan reella tal? Är det likhet mellan vektorer?
Qetsiyah skrev:Aerius skrev:Alla funktioner har inte en antiderivata. Men för dom som har det är det lätt att beräkna integralen över funktionen. Läs på om analysens fundamentalsats för mer insikter om det.
Oj där ser man. Jag trodde att alla funktioner hade en primitiv funktion, men icke sann icke
1. Finn alla naturliga tal x som är sådana att . Vad är svaret?
2. Finn alla heltal x som är sådana att . Vad är svaret?
3. Finn alla reellvärda matriser av typ som är sådana att . Vad är svaret?
4. Finn alla komplexa tal x som är sådana att . Vad är svaret?
Du skriver:
Hur kommer det sig att arean under grafen blir till sträckan? Varför just sträckan?
Jo, man kan t.ex. göra en sortanalys:
Affe Jkpg skrev:Du skriver:
Hur kommer det sig att arean under grafen blir till sträckan? Varför just sträckan?
Jo, man kan t.ex. göra en sortanalys:
Hej!
Bara för att och har samma enhet (i detta fall: längd) så behöver de inte vara lika. Däremot, om de är lika så har de samma enhet.
Albiki skrev:Qetsiyah skrev:Albiki skrev:Qetsiyah skrev:Albiki skrev:Hej Qetsiyah!
Generellt är det ett tecken på att ens kunskap har vuxit när man istället för att få ett svar på en fråga får en ny fråga, fast på ett djupare plan.
Ett exempel: Om jag skulle be dig lösa ekvationen , vad skulle du göra då?
är det en kuggfråga? haha. Jag skulle lösa den på bokstavligen mindre än en sekund utan papper eller penna.
Då visar du att du inte har förstått problemet. Vad handlar ekvationen om?
Jag kan inte ge ett svar som tillför något nytt (tex en närmare förklaring om dess innebörd). Det kan bara bli en totalt intressant översättning mellan matte och svenska. 2x=3 är självförklarande.
Nej, 2x=3 är inte självförklarande. Du gör en massa antaganden här, baserat på din bristande kunskap om matematik.
Ekvationen är bara meningsfull om man tydligt specificerar vad den innebär. Vad betecknar 2? Är det det reella talet 2? (Det behöver det inte vara.) Vad betecknar 2x? Är det multiplikation mellan det reella talet 2 och x? Är multiplikationen definierad? (Det beror på vad x är; om x betecknar reellt tal så är multiplikationen definierad. Men om x är en vektor och multiplikationen är vektoriell produkt så är multiplikationen 2x nonsens om 2 är ett reellt tal.) Vad betecknar likhetstecknet? Är det likhet mellan reella tal? Är det likhet mellan vektorer?
Jag tycker inte att min, enligt dig överanvända, förmåga att göra antaganden är ett tecken på bristande kunskap i matematik, utan snarare på det motsatta. Utav alla möjliga samlingar premisser antog jag att det var det enklaste du menade. Det är i långt ifrån alla fall produktivt att rada upp alla möjligheter och utvärdera sannolikheten att det är just någon av dem som gäller. Att besitta mer avancerad kunskap i matematik kan ge möjligheten till just detta, och det är en konst att tygla den utifrån behov. I detta fall tyckte jag att det varken fanns behov till detta eller att kalla min mattekunskap för bristande.
Albiki skrev:Affe Jkpg skrev:Du skriver:
Hur kommer det sig att arean under grafen blir till sträckan? Varför just sträckan?
Jo, man kan t.ex. göra en sortanalys:
Hej!
Bara för att och har samma enhet (i detta fall: längd) så behöver de inte vara lika. Däremot, om de är lika så har de samma enhet.
Låt oss anta att vi ändå tror på att följande är sant:
För andra tider och hastigheter tror vi då också att:
För tredje tider och hastigheter skriver vi t.ex.:
Eller för att skriva samma sak på ett annat sätt:
Qetsiyah skrev:Albiki skrev:Qetsiyah skrev:Albiki skrev:Qetsiyah skrev:Albiki skrev:Hej Qetsiyah!
Generellt är det ett tecken på att ens kunskap har vuxit när man istället för att få ett svar på en fråga får en ny fråga, fast på ett djupare plan.
Ett exempel: Om jag skulle be dig lösa ekvationen , vad skulle du göra då?
är det en kuggfråga? haha. Jag skulle lösa den på bokstavligen mindre än en sekund utan papper eller penna.
Då visar du att du inte har förstått problemet. Vad handlar ekvationen om?
Jag kan inte ge ett svar som tillför något nytt (tex en närmare förklaring om dess innebörd). Det kan bara bli en totalt intressant översättning mellan matte och svenska. 2x=3 är självförklarande.
Nej, 2x=3 är inte självförklarande. Du gör en massa antaganden här, baserat på din bristande kunskap om matematik.
Ekvationen är bara meningsfull om man tydligt specificerar vad den innebär. Vad betecknar 2? Är det det reella talet 2? (Det behöver det inte vara.) Vad betecknar 2x? Är det multiplikation mellan det reella talet 2 och x? Är multiplikationen definierad? (Det beror på vad x är; om x betecknar reellt tal så är multiplikationen definierad. Men om x är en vektor och multiplikationen är vektoriell produkt så är multiplikationen 2x nonsens om 2 är ett reellt tal.) Vad betecknar likhetstecknet? Är det likhet mellan reella tal? Är det likhet mellan vektorer?
Jag tycker inte att min, enligt dig överanvända, förmåga att göra antaganden är ett tecken på bristande kunskap i matematik, utan snarare på det motsatta. Utav alla möjliga samlingar premisser antog jag att det var det enklaste du menade. Det är i långt ifrån alla fall produktivt att rada upp alla möjligheter och utvärdera sannolikheten att det är just någon av dem som gäller. Att besitta mer avancerad kunskap i matematik kan ge möjligheten till just detta, och det är en konst att tygla den utifrån behov. I detta fall tyckte jag att det varken fanns behov till detta eller att kalla min mattekunskap för bristande.
En person som kan matematik hade sagt att min ursprungliga uppgift (Lös ekvationen 2x=3) var meningslös, eftersom jag inte hade givit någon kontext. Inom matematik kan man inte anta att det är "det enklaste" som avses.
Och vad gäller din mattekunskap, jämfört med en elev i grundskolans årskurs tre är den betydande men jämförd med en person i universitetets årskurs 3 (på matematikprogram) är den blygsam; det är inget fel med det, utan är helt naturligt.
Affe Jkpg skrev:Albiki skrev:Affe Jkpg skrev:Du skriver:
Hur kommer det sig att arean under grafen blir till sträckan? Varför just sträckan?
Jo, man kan t.ex. göra en sortanalys:
Hej!
Bara för att och har samma enhet (i detta fall: längd) så behöver de inte vara lika. Däremot, om de är lika så har de samma enhet.
Låt oss anta att vi ändå tror på att följande är sant:
För andra tider och hastigheter tror vi då också att:
För tredje tider och hastigheter skriver vi t.ex.:
Eller för att skriva samma sak på ett annat sätt:
Nej, det gäller inte att ökningen i är samma sak som ökningen i multiplicerad med ökningen i .
Om så är , vilket inte är samma sak som .
Albiki, du har just en i övrigt tråkig dag mycket bättre. Tack.
Albiki skrev:Affe Jkpg skrev:Albiki skrev:Affe Jkpg skrev:Du skriver:
Hur kommer det sig att arean under grafen blir till sträckan? Varför just sträckan?
Jo, man kan t.ex. göra en sortanalys:
Hej!
Bara för att och har samma enhet (i detta fall: längd) så behöver de inte vara lika. Däremot, om de är lika så har de samma enhet.
Låt oss anta att vi ändå tror på att följande är sant:
För andra tider och hastigheter tror vi då också att:
För tredje tider och hastigheter skriver vi t.ex.:
Eller för att skriva samma sak på ett annat sätt:
Nej, det gäller inte att ökningen i är samma sak som ökningen i multiplicerad med ökningen i .
Om så är , vilket inte är samma sak som .
Om du tittar i v-t-diagrammet, så ser du att inte avser ett differensvärde på det sätt som du vill tolka det.
Figuren är månne opedagogisk för vissa, men jag hittade inget annat.
Qetsiyah skrev:Hej!
Kort version: Jag är förvirrad över var min förmåga att lösa en ekvation algebraiskt (="för hand") slutar när det kommer till trigonometriska (matte4) och diff ekvationer (matte5).
Lång version: Jag har märkt av en sak. Ända sen matte 1 (eller kanske så långt jag kan minnas faktiskt) har vi i skolan lärt oss om att lösa ekvationer. Mer och mer komplicerade sådana, och som hjälp på vägen även fått med regler/formler, det kändes tryggt och inget fanns utom räckhåll (eller jo, men jag visste exakt vad som var utom räckhåll och vi höll oss (som klass, med läraren i spetsen) borta från det). Tex vid matte 2, pq-formeln funkade på allt, och ifall vi stötte på en (då) ovanlig tredjegradare visste vi att där har vi ingen formel (som vi hade lärt oss), så då gällde miniräknare. Det var tydligt var våra begränsningar gick liksom, och vad vi skulle göra när vi såg x (pun intended!).
Men i matte 4 hände något, när vi lärde oss mer om trigonometriska funktioner och ekvationer. Då fanns ingen klassifikation på ekvationerna och det var osäkert vid åsynen av en sådan, om jag ens kunde lösa den. Det var inte alls lika lätt att veta vilka jag kunde/inte kunde läsa. Oftast fanns dock miniräknaren, men det har jag länge ansett vara mindre elegant än att lösa algebraiskt så min första tanke var aldrig att plocka upp den.
Diff ekvationerna i matte5 ska vi inte ens tala om. Jag läste precis på wikipedia att det inte ens finns lösningar på vissa, även om man hade dator/miniräknare. Jag blir förvirrad över vad jag kan och inte kan. Det känns som att jag är i djupt vatten, ingen kontroll. Är detta en bieffekt av att klättra i matten?
Lite så är det. Ju mer man lär sig desto ödmjukare blir man inför vad man inte kan. Det farligaste man kan göra är att tro att man kan allting. Du ska dock inte vara så hård mot dig själv, du går ju bara i gymnasiet. Läser du till exempel en civilingenjörsutbildning så får du ju 5 år av ganska intensiv träning inom det område du väljer och säkert 90 % av alla kurser kommer innehålla någon form av matematik.
Förövrigt är gymnasiematte och fysik inte speciellt förklarande, man får oftast bara lära sig hur man räknar men inte varför.
Kul att läsa det här inlägget, eftersom det visar att du reflekterar kring ditt lärande (metakognition), något alla studenter borde uppmuntras till.
Det brukar vara så att ju mer man kan om ett område desto mer inser man hur lite man faktiskt kan. Jag förstår att det kan kännas som du är ute på djupt vatten men tycker du kan vända det till något positivt. Se det som att du klättrat upp på ett litet gymnasieberg av matematik och blickar ut över ett enormt landskap. Du ser dalar du besökt förut (i dina tidigare kurser) men också nya berg, mycket större än det du nyss bestigit. Det finns också mycket skog som du inte varit nära än, det finns så mycket att uforska!
Problemen man stöter på i Matematikkurserna (och många andra kurser) är oftast mycket tillrättalagda, eftersom de avser att träna en viss teori eller metod. Det blir lätt att man tänker "vilken metod ska jag tillämpa på den här ekvationen". Om jag fortsätter liknelsen ovan, med skogar och dalar, är det som man följer väl valda vandringsleder. Men naturen anpassar sig inte efter dessa leder och väljer man att lämna dem, måste man vara beredd på att stöta på det okända.
Det är sant att det finns många ekvationer som saknar lösning, framförallt analytisk lösning. Detta är vanligt i många ingenjörstillämpningar, men istället söker man efter approximativa och numeriska lösningar. Ekvationer som innehåller trigonometriska funktioner kan snabbt bli mycket komplexa och man tappar kollen på vilka man kan lösa och vilka som saknar lösningar. Så, du är inte ensam om att titta på en ekvation och undra "Kan jag lösa den där?".
Men jag skulle vilja säga att utmaningen är oftast inte att lösa ekvationerna utan snarare att ställa upp rätt ekvationer. Om det inte finns en lösning (inte ens en numerisk eller approximativ) på ett problem, är det snarare en indikation på att man har formulerat ett dåligt problem. Ett löjligt exempel: Jag ska klippa till en kvadrat av papper. Vad ska sidlängden vara om arean ska bli -1 cm^2. Det finns ingen praktiskt användbar lösning till detta problem, och innan man gått igenom komplexa tal finns det ingen lösning alls.
Jag tycker du ska vara optimitisk men också inse att du kommer aldrig känna dig säker inför alla problem, varken inom matematiken eller livet, men det är något bra!
Angående frågan om integralen
Det här blir kanske för krångligt men gör ändå ett försök.
Inom fysik finns det sju grundstorheter, två av dessa är längd och tid . Hastighet däremot är en s.k. härledd storhet.
Vi definierar hastigheten som tidsderivatan av sträckan
Vi har alltså valt att införa ett begrepp som vi kallar hastighet och definierar som sträcka per tidsenhet.
Från detta får vi då att sträckan man rör sig över ett litet tidssteg blir .
Om vi nu räknar ut hastigheten i några punkter, säg i mitten av varje stapel i figuren (kopierade den från tidigare) kan vi för varje stapel skriva medelhastigheten som:
där i syftar på stapel nummer i, och går då från 0 till N. (Vi räknar alltså ut hastigheten som lutningen på s-grafen över en stapel.)
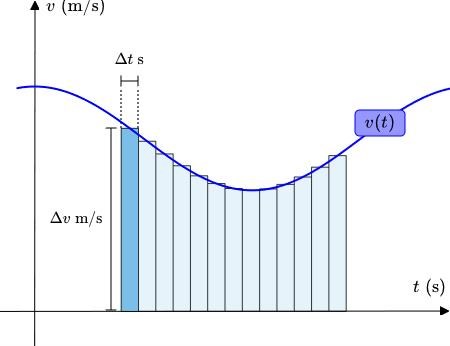
Från uttrycket ovan får vi
- För den första stapeln
- För den andra stapeln
- Osv
- För den sista stapeln
Om vi nu vill räkna ut hela sträckan i slutet, vid tiden löser vi ut genom att kombinera alla ekvationerna i listan, vilket ger
Okej, nu börjar vi komma någonstans!
- Differensen i sträcka är alltså summan av staplarnas area.
- Summan av staplarnas area är en approximation på arean under -grafen (bir bättre med fler staplar).
- Utifrån detta drar vi slutsatsen att arean under grafen blir sträckan.
Kommentarer:
- Låter man staplarna bli oändligt smala blir summan ovan en integral istället.
- Vill förtydliga att integralen blir i det här fallet en sträcka, enbart eftersom vi integrerar en hastighet. Om vi istället integrerar accelerationen, (som också den är en en härledd storhet definierad som tidsdervatan av hastigheten) får vi en hastighet.
Jimbotron skrev:Kul att läsa det här inlägget, eftersom det visar att du reflekterar kring ditt lärande (metakognition), något alla studenter borde uppmuntras till.
Det brukar vara så att ju mer man kan om ett område desto mer inser man hur lite man faktiskt kan. Jag förstår att det kan kännas som du är ute på djupt vatten men tycker du kan vända det till något positivt. Se det som att du klättrat upp på ett litet gymnasieberg av matematik och blickar ut över ett enormt landskap. Du ser dalar du besökt förut (i dina tidigare kurser) men också nya berg, mycket större än det du nyss bestigit. Det finns också mycket skog som du inte varit nära än, det finns så mycket att uforska!
Problemen man stöter på i Matematikkurserna (och många andra kurser) är oftast mycket tillrättalagda, eftersom de avser att träna en viss teori eller metod. Det blir lätt att man tänker "vilken metod ska jag tillämpa på den här ekvationen". Om jag fortsätter liknelsen ovan, med skogar och dalar, är det som man följer väl valda vandringsleder. Men naturen anpassar sig inte efter dessa leder och väljer man att lämna dem, måste man vara beredd på att stöta på det okända.
Det är sant att det finns många ekvationer som saknar lösning, framförallt analytisk lösning. Detta är vanligt i många ingenjörstillämpningar, men istället söker man efter approximativa och numeriska lösningar. Ekvationer som innehåller trigonometriska funktioner kan snabbt bli mycket komplexa och man tappar kollen på vilka man kan lösa och vilka som saknar lösningar. Så, du är inte ensam om att titta på en ekvation och undra "Kan jag lösa den där?".
Men jag skulle vilja säga att utmaningen är oftast inte att lösa ekvationerna utan snarare att ställa upp rätt ekvationer. Om det inte finns en lösning (inte ens en numerisk eller approximativ) på ett problem, är det snarare en indikation på att man har formulerat ett dåligt problem. Ett löjligt exempel: Jag ska klippa till en kvadrat av papper. Vad ska sidlängden vara om arean ska bli -1 cm^2. Det finns ingen praktiskt användbar lösning till detta problem, och innan man gått igenom komplexa tal finns det ingen lösning alls.
Jag tycker du ska vara optimitisk men också inse att du kommer aldrig känna dig säker inför alla problem, varken inom matematiken eller livet, men det är något bra!
Angående frågan om integralenDet här blir kanske för krångligt men gör ändå ett försök.
Inom fysik finns det sju grundstorheter, två av dessa är längd och tid . Hastighet däremot är en s.k. härledd storhet.
Vi definierar hastigheten som tidsderivatan av sträckanVi har alltså valt att införa ett begrepp som vi kallar hastighet och definierar som sträcka per tidsenhet.
Från detta får vi då att sträckan man rör sig över ett litet tidssteg blir .Om vi nu räknar ut hastigheten i några punkter, säg i mitten av varje stapel i figuren (kopierade den från tidigare) kan vi för varje stapel skriva medelhastigheten som:
där i syftar på stapel nummer i, och går då från 0 till N. (Vi räknar alltså ut hastigheten som lutningen på s-grafen över en stapel.)
Från uttrycket ovan får vi
- För den första stapeln
- För den andra stapeln
- Osv
- För den sista stapeln
Om vi nu vill räkna ut hela sträckan i slutet, vid tiden löser vi ut genom att kombinera alla ekvationerna i listan, vilket ger
Okej, nu börjar vi komma någonstans!
- Differensen i sträcka är alltså summan av staplarnas area.
- Summan av staplarnas area är en approximation på arean under -grafen (bir bättre med fler staplar).
- Utifrån detta drar vi slutsatsen att arean under grafen blir sträckan.
Kommentarer:
- Låter man staplarna bli oändligt smala blir summan ovan en integral istället.
- Vill förtydliga att integralen blir i det här fallet en sträcka, enbart eftersom vi integrerar en hastighet. Om vi istället integrerar accelerationen, (som också den är en en härledd storhet definierad som tidsdervatan av hastigheten) får vi en hastighet.
Tack för ditt svar! Jag ska se till att bli van vid det, och se det positivt.
Angående integralen där så förstår jag resonemanget med de smala rektanglarna, men där jag (och många andra) tappar bort mig är när man tar steget från den oändliga summationen till integralen. Vi associerar ju integraler med funktioner och derivator och så, inte med någon summation, och inte alls med areor av något slag. Hur förklarar du det sista steget där? Är det så att integraler bara är definerade så (som en summation!)?
Ja, just det. En integral är egentligen en oändlig summa av funktionsvärden multiplicerat med ett oändligt litet tal.
Jag gav mig på att försöka förklara varför en sådan oändlig summa kan beräknas med hjälp av antiderivator här:
Ja, integralen kan defineras som ett gränsfall (vet inte om det begreppet ingår i gymnasiemattten) då man låter staplarna bli oändligt små. Det blir då en oändlig summa av oändligt smala staplar. Under Riemannintegral kan man se en definition av integral. Det jag gjorde här ovan var inget formellt bevis, utan snarare en motivering hur man kan tolka resultat.
Att se integraler som summor, skulle jag säga är bland de mest användbara tolkningarna jag lärt mig inom matematiken. Det betraktelsesättet återkommer gång på gång inom fysik och teknik men även finans. Därför rekommenderar jag att träna på att se dem som generaliserade summor.
Jimbotron skrev:Ja, integralen kan defineras som ett gränsfall (vet inte om det begreppet ingår i gymnasiemattten) då man låter staplarna bli oändligt små. Det blir då en oändlig summa av oändligt smala staplar. Under Riemannintegral kan man se en definition av integral. Det jag gjorde här ovan var inget formellt bevis, utan snarare en motivering hur man kan tolka resultat.
Att se integraler som summor, skulle jag säga är bland de mest användbara tolkningarna jag lärt mig inom matematiken. Det betraktelsesättet återkommer gång på gång inom fysik och teknik men även finans. Därför rekommenderar jag att träna på att se dem som generaliserade summor.
Jag har blivit van vid att tänka integraler som motsatsen till derivator, och därför lät det konstigt att integraler hade något med areor att göra. Och då tror jag faktiskt att jag talar för i stort sett alla som har lärt sig om integraler på gymnasiet, för här betyder integral helt enklt antiderivata!
Jag vill inte låta dramatisk, men har matematikavdelningen på Skolverket gjort ett jättestort misslyckade när det gäller specifikt utlärningen av integraler? Jag kan tänka mig att det liksom inte kommer hålla i längden om det är användbart att tänka integraler som areasummationer. Eller kan detta synsätt (i alla fall kortsiktigt) vara bra att lära sig? Skulle man inte kunna lära ut hur man beräknar areor under grafer genom att enbart använda begreppet "antiderivata" och undvika "integraler" om nu det fanns en sån stor skillnad?
Jag har blivit van vid att tänka integraler som motsatsen till derivator, och därför lät det konstigt att integraler hade något med areor att göra. Och då tror jag faktiskt att jag talar för i stort sett alla som har lärt sig om integraler på gymnasiet, för här betyder integral helt enklt antiderivata!
Jag vill inte låta dramatisk, men har matematikavdelningen på Skolverket gjort ett jättestort misslyckade när det gäller specifikt utlärningen av integraler? Jag kan tänka mig att det liksom inte kommer hålla i längden om det är användbart att tänka integraler som areasummationer. Eller kan detta synsätt (i alla fall kortsiktigt) vara bra att lära sig? Skulle man inte kunna lära ut hur man beräknar areor under grafer genom att enbart använda begreppet "antiderivata" och undvika "integraler" om nu det fanns en sån stor skillnad?
Ja, det är väl så man vanligtvis introducerar integraler. I många fall är det värdefullt att se integralen som "bara som en summa", ibland som "arean under grafen" och ibland enbart från definitionen som en "antiderivata". Nu har jag inte funderat så mycket på det här men jag skulle säga att antiderivata handlar mycket om hur man räknar ut integralens värde analytiskt. Se det såhär, om vi kan hitta en primitiv funktion F, ja då kan vi räkna ut integralen, mellan a och b som som skillnaden F(b) -F(a).
Från exemplet jag tog upp ser man också att man inte nödvändigtvis måste bestämma en antiderivata. Att räkna ut integralen som en summa är vad datorer i praktiken gör, där "tar man inte fram en primitiv funktion" (om det inte är symbolhanterande program).
Jag vet inte om skolverket har misslyckats, men jag tycker definitivt att fokus borde vara på att besrkiva vad integraler är och hur de kan tolkas, att traggla på att ta fram massa primitiva funktioner är lite bortkastat med tid (alltså mindre tid, inte ta bort helt).
Att säga att integral är antiderivata är lite förenklat tycker jag. Det är för obetämda integraler (utan integrationsgränser), där man bara är intresserad av en primitiv funktion, som detta är en tillräcklig besrkivning. Med mitt tidigare svar som exempel, "sträckan fås genom att integrera hastigheten" och "hastigheten fås genom att derivera sträckan".
På samma sätt som man säger "derivatan är lutningen på grafen" säger man "integralen är arean under grafen". Men se integraler som summor - det är vad dem är.
Jag är lite förvirrad om vad som hänt i den här tråden. Själva frågan från trådskaparen var ju om hur man organiserar sina kunskaper om vilka problem man kan lösa och om det kunde man ju sagt mycket konkret men sedan inflikas en massa saker om integraler och linkära ekvationer menlite om frågan.
Jag hade ju att förväntat man kunde utforskat någon faktiskt modell eller klassifikation, exempelvis skrivit något om att våra lösbara problem bildar ett slags träd där varje svårare problem förbinds till enklare problem genom enklare omskrivningar och att förmågan att organisera sådana strukturer explicit ger en en överblick över vad man kan.
Gällande att inte kunna veta när de trigonometriska problemen går att lösa hade vi kanske kommit fram till att de lösbara, för hen, förmodligen är de trigonometriska polynomen av låg grad och genom att känna igen dem förstår vilka de olösbara är likt man känner igen skillnaden mellan tredjegradaren och andragradaren men innan man kan skilja dem så vet mam inte begränsningarna hos sina scheman.
SeriousCephalopod skrev:Jag är lite förvirrad om vad som hänt i den här tråden. Själva frågan från trådskaparen var ju om hur man organiserar sina kunskaper om vilka problem man kan lösa och om det kunde man ju sagt mycket konkret men sedan inflikas en massa saker om integraler och linkära ekvationer menlite om frågan.
Jag hade ju att förväntat man kunde utforskat någon faktiskt modell eller klassifikation, exempelvis skrivit något om att våra lösbara problem bildar ett slags träd där varje svårare problem förbinds till enklare problem genom enklare omskrivningar och att förmågan att organisera sådana strukturer explicit ger en en överblick över vad man kan.
Gällande att inte kunna veta när de trigonometriska problemen går att lösa hade vi kanske kommit fram till att de lösbara, för hen, förmodligen är de trigonometriska polynomen av låg grad och genom att känna igen dem förstår vilka de olösbara är likt man känner igen skillnaden mellan tredjegradaren och andragradaren men innan man kan skilja dem så vet mam inte begränsningarna hos sina scheman.
Jag känner att min enkla fråga spårade ur tråden totalt. 😋





.jpg?width=80&crop=0,0,80,80)


