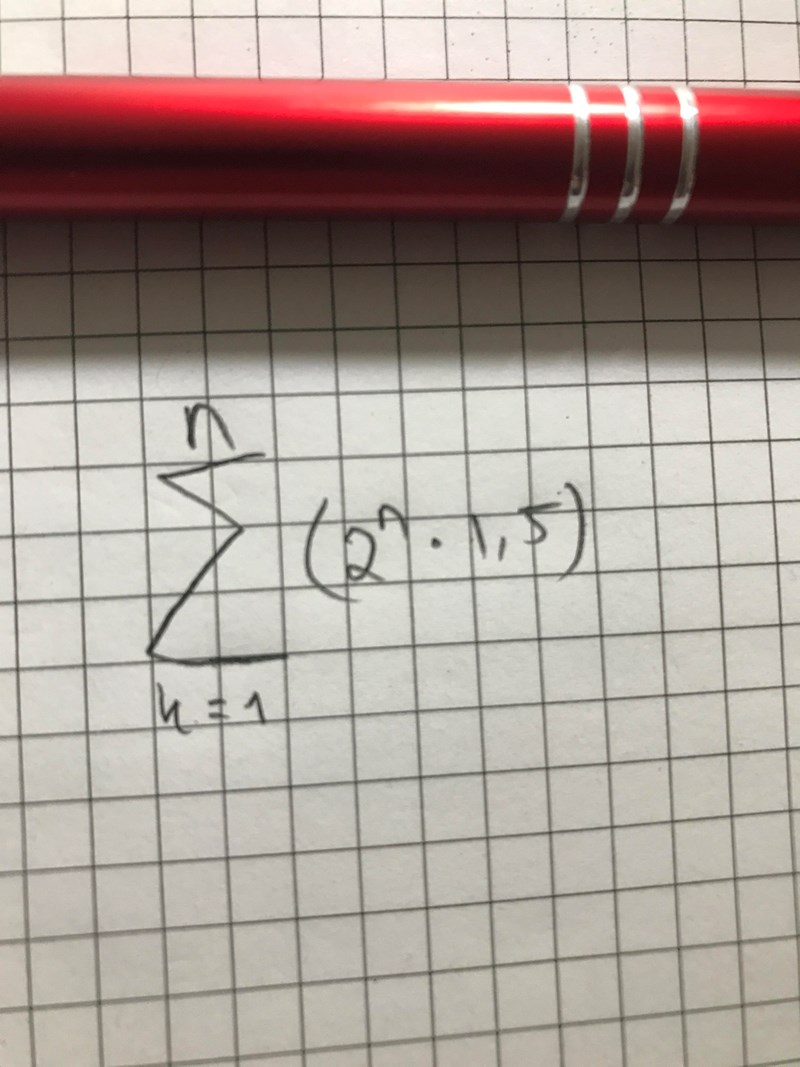
Teckna summan med summatecknet och tillhörande slutna formel

detrr skrev:

Hej, jag behöver hjälp med denna uppgift, både a) och b).

 

Jag vet inte riktigt hur jag ska komma igång för att hitta den slutna formeln. Jag ser ju mönstret, men jag vet inte hur jag ska uttrycka det i en sluten formel. 

Vi börjar med den första, hur ser mönstret ut?

$$\begin{gathered} För n=1 är talet 2 \\ För n=2 är talet 4 \\ För n=3 är talet 8 \\ osv... \end{gathered}$$

Det är en ökning med det dubbla av förgående tal. 

detrr skrev:

$$\begin{gathered} För n=1 är talet 2 \\ För n=2 är talet 4 \\ För n=3 är talet 8 \\ osv... \end{gathered}$$

 

Det är en ökning med det dubbla av förgående tal. 

 Bra. Om du tänker detta med hjälp av förändringsfaktor, hur tänker du då?

Förändringsfaktorn borde då vara 2? 

detrr skrev:

Förändringsfaktorn borde då vara 2? 

Ja, så du kan skriva summan som $2+2*2+2*2*2+2*2*2*2+2*2*2*2*2+2*2*2*2*2*2$. 

(tips: $2*2=2^2, 2*2*2=2^3$ osv)

Okej, då förstår jag a). Formeln blir då $2^n$.

På b) Där ökar det med samma ökning som i a), dvs det dubbla av förgående tal. 

detrr skrev:

Okej, då förstår jag a). Formeln blir då $2^n$.

 

På b) Där ökar det med samma ökning som i a), dvs det dubbla av förgående tal. 

Ja, hela formeln skulle vara $\sum\limits_{n=1}^62^n$.

Gör samma sak för b) så kommer du se hur du kan skriva den summan :)

Jag får det till $2^n$ men det saknas något och först tänkte jag att jag adderar n. Men det funkar inte sen när man kommer till stora tal. 

detrr skrev:

Jag får det till $2^n$ men det saknas något och först tänkte jag att jag adderar n. Men det funkar inte sen när man kommer till stora tal. 

Bra början. Vi prövar lite med $2^n$:

$2^1=2$ men du vill ha 3. Vad ska du multiplicera $2^1$ med för att få 3?

$2^2=4$ men du vill ha 6. Vad ska du multiplicera $2^2$ med för att få 6?

$2^3=8$ men du vill ha ...

Multiplicerar med 1,5. 

detrr skrev:

Multiplicerar med 1,5. 

 Just det. Kan du då skriva den slutna formeln?

$2^n · 1,5$

detrr skrev:

$2^n · 1,5$

Ja, det där är den n-te termen i summan.

Kan du då skriva ett uttryck för hela summan?

så?

detrr skrev:

 

så?

Nej nu blandar du ihop det.

Till att börja med är det 7 termer du ska summera i b-uppgiften så summan ska gå från 1 till 7.

Sen är det n du ska använda som summavariabel och inte k.

Dvs du ska summera termerna $1,5·2^n$ från $n=1$ till $n=7$

Aha ibland brukar det stå i min mattebok både k = t ex 1 och sen n överst. Vad betyder det? Är det att k ska gå från 1 till vilket tal som helst? 

detrr skrev:

Aha ibland brukar det stå i min mattebok både k = t ex 1 och sen n överst. Vad betyder det? Är det att k ska gå från 1 till vilket tal som helst? 

Typ, men då står det där n någonstans före eller efter i texten också.

Okej, då förstår jag. Tack för hjälpen! :)