Termodynamik

Termodynamikens första lag. Hur lyder den?

Titta på figuren från kontrollfråga 5 gällande första lagen.

Svara på fråga a) b) och c) och förklara med egna ord varför du rankar dem i den ordning du gör.

Tack så mycket ConnyN och förlåt för ett sent svar!

Ok. 

Jag tänker att ändringen i inreenergi är som störst när både tryck och volym ökar? Därför att $\displaystyle dU= dQ+PV$. Så $4, 3, 2, 1$?

På arbetet tänker jag att integralen under kurvorna avgör vilket system uträttar störst arbete. Så då blir det också $4, 3, 2, 1$?

På värme transport vet jag inte riktigt :( Vad jag vet är att om $T$ som tilllförs i systemet är större än $T$ som systemet har så får vi transport av värme.

Den första är lurig, men om man kommer ihåg att inre energi är en tillståndsfunktion blir svaret ganska lätt.

På b) verkar du ha tänkt rätt.

Du kan utnyttja svaren i a) och b) för att svara på c) med hänvisning till termodynamikens första huvudsats. Ändringen i inre energi säger hur mycket energi som fördes ut ur systemet. Första huvudsatsen säger att denna energi antingen måste ha lämnat i form av arbete eller värme.

Då är den Inreenergin densamma för alla 4?

Exakt!

Okej tack! Visste inte att inre energin var en tillståndsfunktion!

Så i c) utgår jag från $\displaystyle \delta U=Q+W$ och då blir det så att den väg med minst arbete som transporterar minst värme? :/

Om du sänker den inre energin lika mycket i samtliga fall innebär det att du behöver leda bort lika mycket energi i de olika fallen. Du vet att energin måste transporteras bort som arbete eller värme och den energi som inte blir arbete måste bli värme. Du vet vilka som uträttar mest arbete, så du kan då konstatera vilka som måste leda bort mer energi i form av värme.

Står du fast vid att de som uträttar minst arbete också utvecklar minst värme?

Tack så mycket Teraeagle. Det ska vara tvärtom!

Fler uppgifter, tack! :)

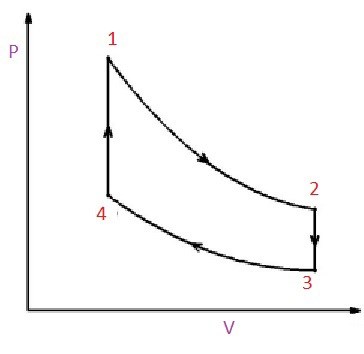
Föreslå minst två sätt att öka verkningsgraden för en värmemaskin som arbetar enligt denna cykel:

Som jag skrev i ett PM till dig Soderstrom så har jag inte kommit till termodynamikens lagar i mina studier, men du har fått bra hjälp av Teraeagle och ni har tillsammans rett ut begreppen bra och kommit fram till rätt svar enligt facit i min bok.

Vad jag möjligen saknar är att du kunnat förtydliga genom att skriva ut formeln  $∆E_{int}=E_{int,f}-E_{int,i}=Q-W$
Där E_int står för inre energi och f står för "final" och i står för "initial"
Här har jag använt lärobokens beteckningar eftersom jag inte kan de svenska beteckningarna.
Jag misstänker att  $\delta U$är detsamma som $∆E_{int}$

Ett citat ur läroboken "All other combinations of Q and W, including Q alone, W alone, Q+W, and Q-2W, are path dependent;
only the quantity Q-W is not."

Även texten för första lagen bad jag att du skulle skriva ut. I den här läroboken formulerar man den så här:
"The internal energy E_int of a system tends to increase if energy is added as heat Q and tends to increase if energy is lost as work W done by the system."

Tack till er bägge som tog er an uppgiften. Det blir intressant att följa fortsättningen, men jag har inte rätt kunskaper för att kunna vara till någon större hjälp.

Lycka till Soderstrom i din strävan att klara tentan!

ConnyN skrev:

Jag misstänker att  $\delta U$är detsamma som $∆E_{int}$

Nästan, men inte riktigt. U brukar mycket riktigt användas för att beteckna inre energi, likaså E_int. Man använder olika beteckningar i olika böcker. 

Den stora skillnaden är lilla och stora delta. Båda anger att det är en skillnad i inre energi, men lilla delta $\delta$ anger en oändligt liten ändring, medan stora delta $\Delta$ anger en ändring mellan två olika tillstånd, vilka som helst.

Teraeagle skrev:

ConnyN skrev:

Jag misstänker att  $\delta U$är detsamma som $∆E_{int}$

Nästan, men inte riktigt. U brukar mycket riktigt användas för att beteckna inre energi, likaså E_int. Man använder olika beteckningar i olika böcker. 

Den stora skillnaden är lilla och stora delta. Båda anger att det är en skillnad i inre energi, men lilla delta $\delta$ anger en oändligt liten ändring, medan stora delta $\Delta$ anger en ändring mellan två olika tillstånd, vilka som helst.

Aha! Det hade jag ingen aning om. Tack för informationen 👍

Teraeagle skrev:

Föreslå minst två sätt att öka verkningsgraden för en värmemaskin som arbetar enligt denna cykel:

Verkningsgrad är $\displaystyle \eta = \frac{W}{Q}$ 

Så jag tänker att om vi ökar mängden arbete (i det här fallet arean under grafen?) Eller så kan vi också minska värme som vi tillför i värmemaskinen och då gör vi det genom att minska volym? :/

Känner mig säkrare på första förslaget! 

PS angående stora delta och lilla delta så menade jag egentligen $\Delta$ :)

Absolut, om arbetet ökar mer i förhållande till värmeflödet så ökar verkningsgraden, men vad ska man ändra rent konkret? Temperaturer, tryck, volymer?

Vad menar du när du skriver arean under grafen? Skulle du kunna rita i figuren och markera vilken area som motsvarar arbetet?

Jag tänker det rödmarkerade området motsvarar arbetet i det här fallet (?). 

Sen vet jag inte hur man ska tolka diagrammet. Från 1 till 2. Vad händer där? Från 2 till 3? Osv... :(

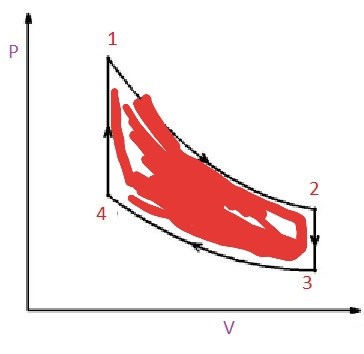
Mycket riktigt.

1–>2 motsvarar en isoterm (konstant temperatur) expansion där systemet utför ett arbete.

2–>3 motsvarar en isokor (konstant volym) avkylning där temperaturen och trycket sjunker.

3–>4 motsvarar en isoterm kompression där omgivningen utför ett arbete på systemet.

4–>1 motsvarar en isokor (konstant volym) upphettning där temperaturen och trycket stiger.

När systemet utför ett arbete på omgivningen motsvarar det arean under kurvan 1–>3 ner till V-axeln och när omgivningen utför ett arbete på systemet motsvarar det arean under kurvan 3–>4 ner till V-axeln. Nettoarbetet motsvarar skillnaden mellan dessa, vilket då blir det inringade området.

Kolla gärna upp Carnots teorem:

https://en.wikipedia.org/wiki/Carnot%27s_theorem_(thermodynamics) 

Där ser du att man kan ändra verkningsgraden genom att justera temperaturerna. 

Okej! Tack så mycket! Så alltså för att öka $\eta$ så måste vi införa mer värme $T_{h}$ och öka nyttig arbete. Är det svar på din fråga, Teraeagle? :)

Jag tror att du tänker rätt med skriver fel, du menar väl att man kan öka temperaturen vid expansionen, eller hur? Då kommer du att få en högre verkningsgrad, allt annat lika.

Kan du göra något åt temperaturen vid kompressionen?

Då ska man minska temperaturen för att systemet kommer att transportera värme? :)

Bump :(

Det stämmer att du kan sänka temperaturen, men du måste träna på att uttrycka dig mer vetenskapligt och använda rätt begrepp. Jag förstår att du tänker rätt, men du skriver inte det du tänker. 

Svaret är alltså att du kan höja temperaturen vid expansionen eller sänka temperaturen vid kompressionen för att få en högre verkningsgrad. Rent grafisk motsvarar det att du får ett större inringat område i pV-diagrammet.

Här får du en ny fråga: Växter tar upp små, lättrörliga molekyler med hög entropi som koldioxid och vatten och omvandlar dem till stora, komplexa föreningar som stärkelse och cellulosa som har lägre entropi. Förklara varför detta inte bryter mot termodynamikens andra huvudsats.

Sorry men vi har aldrig pratat om växter och sånt i föreläsningarna, men jag antar att det bara är ett vanligt exempel? :)

Du kan väl tillämpa dina kunskaper på annat förutom exemplen i en bok eller en föreläsning?

Teraeagle skrev:

 

Här får du en ny fråga: Växter tar upp små, lättrörliga molekyler med hög entropi som koldioxid och vatten och omvandlar dem till stora, komplexa föreningar som stärkelse och cellulosa som har lägre entropi. Förklara varför detta inte bryter mot termodynamikens andra huvudsats.

Det bryter inte mot huvudsatsen därför att Entropin $S_{1}$ har inte minskat i de ursprungliga molekylerna. Men de nya stora molekylerna har sina egna entropimängd $S_{2}$ som är då lägre. 

Känns som att svaret inte duger :/

Tänk på vad som är systemet och omgivningen i det här fallet och kom ihåg hur andra huvudsatsen lyder.

Systemet är växter i det här fallet? Andra huvudsatsen säger att ett isolerat systems entropi aldrig minskar; isolerade system tenderar att utvecklas mot termodynamisk jämvikt, ett tillstånd av maximal entropi.

Systemet är växten. Solskenet ingår inte i systemet.

Det är ett sätt att uttrycka andra huvudsatsen, men eftersom en växt inte är ett isolerat utan ett öppet system (den kan utbyta både materia och energi med omgivningen) är det bättre att uttrycka huvudsatsen som ”universums entropi kan aldrig minska”. Universum är systemet och omgivningen tillsammans. 

Om växten är vårt system och entropin sjunker vid processerna som sker inne i växten, hur kan den göra för att fortfarande uppfylla andra huvudsatsen?

Växten ger ifrån sig energi? Jag tänker att om entropi minskar så måste något annat öka. Och det är energin?

Växten ger ifrån sig energi?

Nej, tvärtom.

Soderstrom skrev:

Växten ger ifrån sig energi? Jag tänker att om entropi minskar så måste något annat öka. Och det är energin?

Du är på rätt spår.

Okej, tack så mycket! Jag minns att jag sett en video som tog upp en liknande exempel typ, och då sa han något med stil att "om entropin minskar så måste något annat öka". Typ så. Men jag tittade inte på videon igen när jag fick denna fråga :)

Fler uppgifter? Tack.

Soderstrom skrev:

Okej, tack så mycket! Jag minns att jag sett en video som tog upp en liknande exempel typ, och då sa han något med stil att "om entropin minskar så måste något annat öka". Typ så. Men jag tittade inte på videon igen när jag fick denna fråga :)

Fler uppgifter? Tack.

Det är samma princip som gör att man kan mätta fler människor om de åt majs, istället för att ge majsen till grisar och sedan äta grisarna. För att en organism ska kunna bygga upp och reparera sig själva med kemiska reaktioner som sänker entropin måste de avge värme till omgivningen, vilket gör att energi måste förloras i varje steg i näringskedjan. 

Ny uppgift:

Förklara vad som händer om man slänger ut en liter 25-gradigt vatten i rymden.

Vattnets temperatur kommer att minska? 

Varför och vad händer?

Det kanske är irrelevant men jag tänker att vattenmolekylerna är i termiskjämvikt med omgivningen. Entropin i vattnet minskar?

Är de verkligen i termisk jämvikt? Det betyder att vattnet har samma temperatur som rymden. 

Börja med att konstatera att trycket är extremt lågt i rymden, nästan ett vakuum. Vad händer om en vätska placeras i ett vakuum?

Dess temperatur kommer att stiga?

Angående termisk jämvikt. Jag tänkte att efter ett tag kommer omgivningen och vätskan ha samma temperatur :)

Hur tänker du att temperaturen stiger?

På grund av att vattnets molekyler har kinetisk energi?

EDIT: Kanske också att vattnets kokpunkt blir lägre i lågt tryck?

Får vattnets molekyler mer rörelseenergi när de slängs ut i rymden? Detta skulle behövas för att temperaturen skulle stiga.

Det stämmer att kokpunkten blir lägre vid lågt tryck, så vattnet börjar koka även fast det har samma temperatur. 

Vad händer med vattnets temperatur när det börjar koka? Tänk på att detta i princip är en helt adiabatisk process.

Vattnets temperatur stiger. Och det innebär att vattnet får mer rörelseenergi då vi också har en adiabatisk process. 

Måste man tillföra eller ta bort energi för att något ska koka?

Nej. Men jag vet inte hur annars :(

Det krävs värme för att något ska koka, men detta är i princip en helt adiabatisk process. Det betyder att värmet tas från vattnet, så att vattnets temperatur sjunker i takt med att det kokar. Till slut når temperaturen fryspunkten och då fryser vattnet till is. Sedan sjunker isens temperatur sakta i takt med att isen strålar ut värme i rymden. Det är alltså inte riktigt en adiabatisk process.

Detta är anledningen till att det finns ganska mycket is i rymden. Flytande vatten kokar helt enkelt bort tills det fryser och blir till is.

Blir inte vattnet ånga när det kokar? 

Jo, men det som blir kvar fryser till is.

Okej! Tack! 

Fler uppgifter? 

Tänkte lite på kursens mål och så men nu är det ju en muntlig examination så det kan variera?

Bump

Bump :/

Ska jag skapa en ny tråd? Verkar som om ingen går igenom 50 svar :/

Rita valfri kretsprocess och beskriv hur den fungerar.

Sorry för sent svar! Jag var upptagen med annat under de senaste dagarna :(

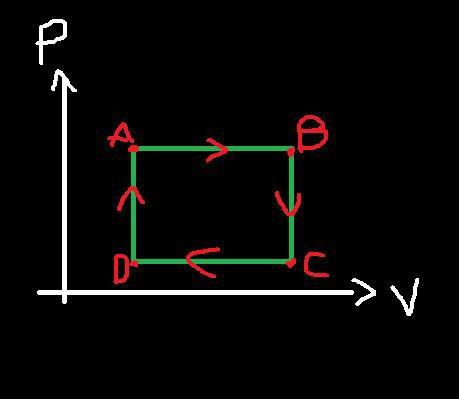
Ok! Jag har ritat en kretsprocess som fungerar så som bilden visar.

Från A-B sker en expansion då volymen ökar med konstant tryck. Så då utövar systemet ett arbete på omgivningen och värme tillförs till systemet på grund av konstant tryck.

Från B-C minskar trycket och volymen hålls konstant, och det händer genom att systemet lämnar ifrån sig värme.

Från C-D sker en kompression där volymen minskar och trycket hålls konstant, det innebär att arbete tillförs till systemet och och värme bortförs från systemet.

Från D-A ökar hålls volymen konstant och trycket höjs, det innebär att värme tillförs i systemet.

Kan det stämma? Kan man rita vilken cykel som helst, typ en cirkel? 

Bump

Det verkar rätt. Du borde rent teoretiskt kunna rita en cirkel, men det är inte säkert att det rent praktiskt går att konstruera en sådan process.

Fler uppgifter, tack.

Bump

Bump :/

Bump :(

Kolla upp gratis engelska böcker som kanske innehåller frågor?

Har bara kursboken. Har du några? 

Nääeee men sök bara "thermodynamics"? Ladda sen ner boken digitalt. Kolla själv om boken täcker det ni lärt er.