Tillämpa Steiners sats på system av flera massor
Halloj!
Jag studerar följande exempel från en gammal tentamen i Mekanik:
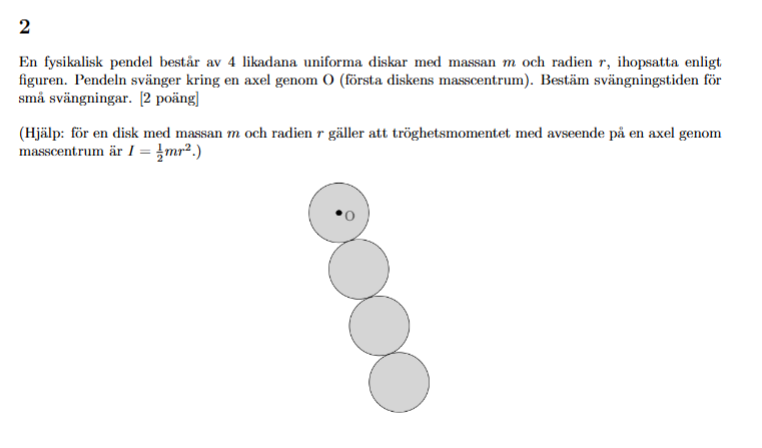
Vi får veta att varje disk med avseende på en axel genom det egna masscentret har tröghetsmoment:
.
Några frågor:
- Avses här en axel som "pekar ut mot läsaren"? Alltså någon typ av -axel om det vi kollar på är ett -plan ovanifrån?
- Jag förstår att man ska tillämpa Steiners sats för att få fram den sammansatta kroppens tröghetsmoment med avseende på . Men hur kan de enskilda kropparna ha något tröghetsmoment alls med avseende på sina egna masscentren? De roterar ju inte kring dessa. För att man ska ha ett tröghetsmoment måste man väl också ha en vinkelhastighet?
EDIT: eller ska man tänka att de roterar kring sina egna masscentren också eftersom de uppenbarligen har ett tröghetsmoment?
naytte skrev:
- Avses här en axel som "pekar ut mot läsaren"? Alltså någon typ av -axel om det vi kollar på är ett -plan ovanifrån?
Precis så.
- Jag förstår att man ska tillämpa Steiners sats för att få fram den sammansatta kroppens tröghetsmoment med avseende på . Men hur kan de enskilda kropparna ha något tröghetsmoment alls med avseende på sina egna masscentren? De roterar ju inte kring dessa. För att man ska ha ett tröghetsmoment måste man väl också ha en vinkelhastighet?
EDIT: eller ska man tänka att de roterar kring sina egna masscentren också eftersom de uppenbarligen har ett tröghetsmoment?
Det är precis detta som man gör med Steiners. Man kollar på tröghetsmomentet runt en axel i deras mc och sedan adderar man tröghetsmomentet som krävs i och med förflyttningen från mc.
Men bara för att förtydliga vad jag funderade på: det är väl inte så att dessa mindre massor roterar kring sina egna masscentra samtidigt, utan satsen säger oss bara något om tröghetsmomentet vid rotation kring godtycklig axel GIVET att vi vet vad tröghetsmomentet för rotation skulle vara runt en med denna parallell axel som går genom masscentret?
T.ex. som här:
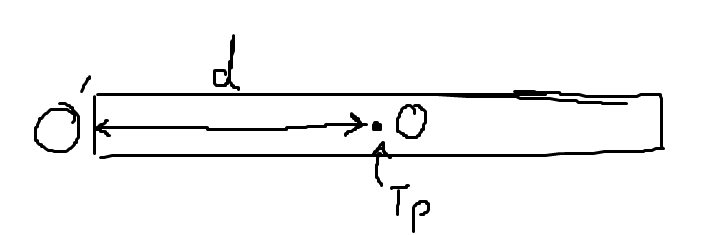
Här har vi en unifrom träbit med massa . Vi vet att tröghetsmomentet runt tyndpunkten är . Då säger Steiners sats att om vi ISTÄLLET skulle vilja ha rotation runt skulle vi ha tröghetsmoment ? För den kan ju inte rotera kring båda axlarna samtidigt, menar jag.
Jaha okej. Nää precis, man ser systemet som en stel kropp. Om det funnit ett passande och enkelt sätt att beräkna tröghetsmomentet för denna kropp direkt hade man gjort det. Men nu råkar att dela upp i delkroppar och använda Steiners vara den bästa metoden vi har.
Men om man har en stel kropp som består av diskreta delmassor, ges inte hela kroppens tröghetsmoment då av:
där betecknar avståndet från varje diskret delmassa till rotationsaxeln?
Varför ska man i så fall använda Steiners sats? Vi har ju alla , ...?
Tillägg: 19 maj 2025 21:25
Eller detta kanske endast gäller partiklar utan utbredning i rummet...
Ja, precis. Det gäller bara för punktmassor.



