Tjej med massa m som glider ned för en rutschkana - bestäm maximal normalkraft
Halloj!
Jag sitter med uppgiften nedan:

Jag har försökt lösa uppgiften på följande vis:
Vi börjar med att konstatera att normalkraften kan beräknas enligt, där är kraften som ritas in i bilden nedan:
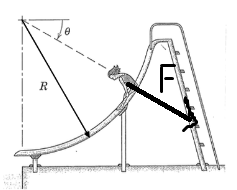
Jag tänker att man lokalt kan approximera rutschkanan som ett lutande plan med någon vinkel mot horisontalplanet. I så fall har vi bilden nedan, för varje punkt:
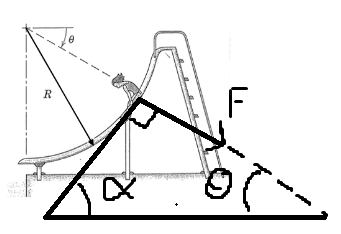
Det är meninginen att vektorn och den streckade förlängningen ska ligga i linje med den streckade linjen från flickan till cirkelcentrum.
Utifrån bilden så avläser jag att . När det kommer till hastigheten avläser jag att den drivande kraften nedför vårt "lutande plan" är . Detta ger accelerationen . Detta ger slutligen:
Detta är dock felaktigt, eftersom det ger en maximal normalkraft vid . Det är uppenbart att normalkraften måste vara maximal vid , så något har blivit knasigt här. Hjälp skulle uppskattas!
naytte skrev:Vi börjar med att konstatera att normalkraften kan beräknas enligt, där är kraften som ritas in i bilden nedan:
Vad hände med tyngdkraften?
Jag ritade inte in den eftersom jag ville ha de krafter som pekar rakt in i och rakt bort ifrån cirkelcentrum (eftersom det handlar om en centripetalkraft). Jag tänker att blir tyngdkraftens komposant i detta "led" (bort från och in i cirkelcentrum).
Menar du att jag har missat att ta med någon kraft i mitt uttryck?
naytte skrev:Jag ritade inte in den eftersom jag ville ha de krafter som pekar rakt in i och rakt bort ifrån cirkelcentrum (eftersom det handlar om en centripetalkraft). Jag tänker att blir tyngdkraftens komposant i detta "led" (bort från och in i cirkelcentrum).
Menar du att jag har missat att ta med någon kraft i mitt uttryck?
Det var oklart vad du menade med F. Om det var flickans radiella kraft på rutschkanan är den förstås lika med normalkraften.
Det var oklart vad du menade med F.
Okej, fattar!
Jag tror åtminstone det är rätt att sätta , för det fick även uppgiftsmakaren i facit, alltså uttrycket:
Men det verkar bli fel när jag försöker bestämma uttrycket för hastigheten (eller i mitt fall bara )
Tillägg: 22 apr 2025 18:48
Jag tror jag fattar nu. är accelerationen som pekar inåt, inte accelerationen som är tangentiell mot cirkelbanan! Det var därför det blev fel; jag tänkte att gav den tangentiella accelerationen...
Du kan räkna ut v mha av den mekaniska energins bevarande.
naytte skrev:Jag tänker att man lokalt kan approximera rutschkanan som ett lutande plan med någon vinkel mot horisontalplanet.
Det blir nog bättre att lösa det på samma sätt som en flicka i en gunga.
Jag har aldrig räknat på en gunga tidigare.
Hur som helst skulle jag vilja försöka använda mekaniska energins bevarande enligt PATENTERAMERAs förslag. Det gäller ju att . Jag vet däremot inte hur jag ska bestämma . Skulle jag kunna få lite vägledning? Helst utifrån bilden som gavs i uppgiften.
EDIT: jag kom på själv hur man kunde göra. Jag behöver glukos...
Det blir , inte sant?
Ja, eller med omvänt tecken, för att få positivt värde.
Yes, då får jag rätt funktion!
Tack för hjälpen!
Jag är lite fundersam kring vad resultatet innebär. Om vi sätter blir uttrycket:
Detta är alltså större än "normalkraften" i varje punkt då man tänker att varje punkt utgör ett till cirkelbågen "tangentiellt, lutande plan". Hur kan det vara så?
Startvinkeln skulle vara strikt större än 0.
Jag förstår inte riktigt vad du menar med din fråga.
Jag funderar bara på vad som skulle hända om starvinkeln vore 0.
Det jag försöker göra är att ta en slags "snapshot" i varje ögonblick under färden, och analysera vilka krafter som verkar just då. Tanken är att approximera varje punkt i banan som ett lutande plan, alltså tänka att flickan i varje ögonblick rör sig en infinitesimalt liten sträcka nedför ett plan med en viss lutningsvinkel (som varierar beroende på var hon är i banan).
Låt oss utgå från bilden nedan:
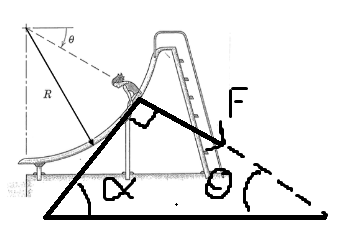
Här har jag försökt rita det jag menar så gott som går i en punkt. Om vi analyserar det här lutande planet så får vi att normalkraftens storlek är . Denna analys blir likadan oavsett av i vilken punkt man analyserar flickan. Således verkar det rimligt att normalkraften i sig skulle vara , om vi saknar startvinkel.
Denna funktion blir dock tre gånger för liten i varje punkt!
Hur kan det bli så? Det jag misstänker är att summan av de infinitesimala felen man får i slutänden blir ändliga och att det är därför det skiter sig, men jag är inte säker.
Hoppas att frågan framgick nu!
Tillägg: 22 apr 2025 22:04
Jag tror problemet är att den analysen inte tar hänsyn alls till att kurvan är böjd; man får inte med någon information om bågens kurvatur. Man måste få med det på något sätt för att en sådan analys skulle fungera.
Tillägg: 22 apr 2025 22:37
Man borde kunna ställa upp N+dN = mgsin(dtheta+theta) och sedan använda additionsformeln för sin, McLaurin-utveckla och sedan integrera, men det blir knas för man får en integral utan differential.
Jo, krökningen är viktig att få med.
Enklast är väl att använda Newtons andra lag i normalriktningen.
man = .
Där an = v2/R = .
Ja, precis. Men om vi skulle försöka spinna vidare på resonemanget som jag föreslog så tänkte jag att man skulle få med krökningen genom att ta hänsyn till ett infinitesimalt vinkelelement (alltså att vinkeln ändras infinitesimalt hela tiden). Det fungerade dock inte riktigt, för trots att man tänker att vinkeln förändras över tid får man inte med krökningen av någon anledning:
Kanske kan konstanten rädda oss på något sätt? :(
Jag förstår bara inte varför detta inte fungerar. Känns högst orimligt.
Jag förstår inte varför du tror att det skulle fungera. Du antar att förändring av normalkraften är lika med förändring av tyngdkraftens normalkomponent. Men då borser du ju helt från att det finns en acceleration.
Men är det inte accelerationen som gör att tyngdkraftens normalkomposant förändras? Om flickan inte hade accelererat inåt mot cirkelcentrum hade det inte heller skett någon förändring i vinkeln.
Jag vet inte varför man inte får med krökningen om man gör som jag försökte ovan, men ett mer explicit sätt kanske kan vara att försöka få med krökningen genom att titta på hur vinkeln förändras med cirkelbågen, alltså:
Det är två "lagar" som styr:
1) Hastigheten v bestäms av mv2/2 = mgh, där h är R(sin fi -sin fi0), d v s v2/R=2g(sin fi -sin fi0)
Normalkraften är summan av massan gånger (tyngdaccelerationen vinkelrätt mot banan, plus 2) accelerationen mot centrum orsakad av cirkelrörelsen, v2/R) d v s m ( g sin fi +2g (sin fi - sin fi0), ett resultat som redan uppnåtts ovan
Om fi0= 0 så blir normalkraften längst ner 3mg d v s man "känner sig" tre ggr så tung.
På en del nöjesfält finns berg- och dalbanor som har en "loop" d v s man far i någon punkt "upp och ned". Hur högt upp i termer av "loopens" radie måste man starta för att fortfarande utöva ett tryck mot vagnens säte vid toppen av "loopen"?
Hur blir det om rutschbanan är parabelformig och inte cirkelformig, d v s har en starkare krökning, mindre radie längst ner?
hansa skrev:accelerationen mot centrum orsakad av cirkelrörelsen, v2/R
Lite petig kanske, men det är tvärtom: cirkelrörelsen orsakas av normalkraften.
(Det är nog tydligare om det är spänningen i ett snöre.)
naytte skrev:Jag vet inte varför man inte får med krökningen om man gör som jag försökte ovan, men ett mer explicit sätt kanske kan vara att försöka få med krökningen genom att titta på hur vinkeln förändras med cirkelbågen, alltså:
Här min härledning.







