Tolka facit/lösningsförslag (Convergence in probability)
Hej, jag skulle behöva hjälp med att tolka facit jag fått givet till a-uppgiften nedan:

"Facit" som vi fått givet är handskrivet men det är vissa steg som jag inte förstår, bifogar facit nedan
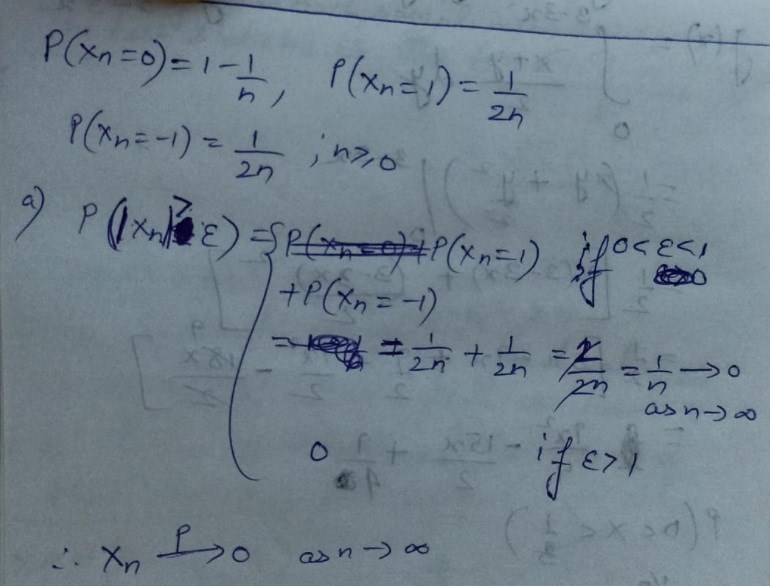
Det jag inte förstår är varför de plussar ihop P(Xn=1) och P(Xn=-1) och hur de får detta för 0<epsilon<1? Är det någon som förstår detta lösningsförslag och har lust att hjälpa mig att förstå det?
Bör man egentligen inte kunna hitta vilken fördelning X har med hjälp utav relationerna vi har givna och därifrån lösa denna?
Hej!
Om så gäller att eftersom , då bara kan anta värdena , och . Vi antar även att , så att fallet inte är intressant. Om vi är lite noggrannare och kallar utfallsrummet för och låter så får du att
.
kan ju inte vara positiv och negativ samtidigt, därför kan du dela upp ditt utfallsrum som där alla är disjunkta mängder. Dessutom gäller för alla att , alla att och såklart även tillsist att alla att .
Moffen skrev:Hej!
Om så gäller att eftersom , då bara kan anta värdena , och . Vi antar även att , så att fallet inte är intressant. Om vi är lite noggrannare och kallar utfallsrummet för och låter så får du att
.
kan ju inte vara positiv och negativ samtidigt, därför kan du dela upp ditt utfallsrum som där alla är disjunkta mängder. Dessutom gäller för alla att , alla att och såklart även tillsist att alla att .
Tack för en bra och tydlig beskrivning, detta klargjorde väldigt mycket!
Jag har dock en fråga, det är fortfarande inte riktigt helt tydligt för mig varför samt adderas? Är det för att det finns två stycken där absolutbeloppet av är lika med 1? Och är det felaktigt att räkna en i taget och inte addera dessa? Då får man istället två stycken där när .
Jag förstår att det inte är helt tydligt. Jag tycker nog inte riktigt att sådana här frågor är helt lämpliga utan att man läst lite måtteori, tiden borde kunna läggas på något bättre (om det nu inte är en kurs i måtteori med en del sannolikhet det vill säga).
Här är alltså ett sannolikhetsmått, det vill säga någonting som mäter storlek på en viss mängd. I ditt fall har du att vi vill mäta hur stor är egentligen mängden som ger utfallen , alltså hur "många" sådana finns det. Så det vi gör är att vi kollar helt enkelt hur många det finns som ger och mäter dess storlek, och sen gör vi likadant och ser hur många det finns som ger . Vi kommer inte att "dubbelräkna" något, det finns ju inte ett enda utfall som kan ge både och .
Jag är inte helt med på din sista mening, men när du skriver så räknar du ju redan båda?
Och för att svara på din första fråga, ja, dom adderas eftersom antas både då och . Ingenting dubbelräknas här heller.
Tack för ditt svar! Kursen är Sannolikhetsteori II och inte måtteori men ska läsa på lite om detta för att se om det ger mig en ökad förståelse!
Det jag menade med min sista mening är att jag antog att då vi vill ha absolutbeloppet av och då så räcker det att beräkna för endast en utav dessa, då får vi följande:
när för .
Men om dessa ska adderas kommer det istället att bli för , som för övrigt kommer att ge samma resultat men då känns mitt antagande felaktigt?
Njaej. Det gäller ju inte att .
Men såklart, om båda är konvergenta och ingenting skumt händer så gäller i allmänhet att gränsvärdet av en summa är summan av gränsvärdena. Men jag vet inte varför du skulle vilja krångla till det så, istället för att bara beräkna summan.
Uttryckte mig nog lika otydligt, menade mer att var en applicering av , men ser nu också (tack vare dina förklaringar) varför man bör beräkna summan och att de även underlättar. Stort tack för din hjälp!

