Trapetsmetoden på tangensfunktion?
Halloj.
Har i uppgift att beräkna mha trapetsmetoden. Själva förfarandet känner jag mig ganska säker på, men det som gör mig förvirrad är funktionen. När jag skriver in funktionen i GeoGeobra så har ju tangens lodräta asymptoter, hur ska jag kunna beräkna arean då? Tangens värde går väl mot oändligheten? Hade ju varit lite enklare om man fått en skiss av funktionen.
Tangens är periodisk med sina 180 grader, men antar att denna funktionens period är 60 grader?
Bökig uppgift.
Hej!
En bild av funktionens graf (ritad med hjälp av Desmos) visar att funktionen har en vertikal asymptot Det betyder att integrationen inte får ske över ett intervall som innehåller detta värde. Gör såhär istället: Omge talet med ett litet intervall () och integrera över intervallet Välj till exempel där är ett stort heltal och använd Trapetsmetoden för att approximera integralen
Låt sedan och se vad som händer med approximationen; om approximationerna har ett ändligt gränsvärde när så är detta gränsvärde en approximation till integralen
Tack för svar! Förstår dock inte helt. När N går mot oändligheten (math equation funkar inte just nu) så kommer ju 1/N vara försumbart? Ser föresten nu att läraren vill att intervallet ska delas upp i 8 delintervall...
Visserligen kan du få ut ett värde med trapetsmetoden och 8 delintervall, men integralen är divergent.
Ehm divergent?
SigTer skrev:Ehm divergent?
Det betyder att integralen inte är ändlig. Exempelvis som följande integral:
tomast80 skrev:SigTer skrev:Ehm divergent?
Det betyder att integralen inte är ändlig. Exempelvis som följande integral:
Okej. Och det är precis det jag inte förstår. Hur ska man kunna approximera ett värde där integrationsgränserna är oändliga? Fårstår inte helt Albikis förklaring.
T ex denna bild:
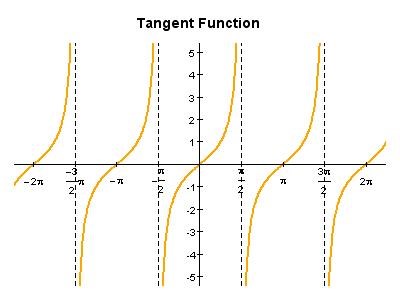
Funktionen för Tan X. Här ser man att funktionen har en vertikal asymptot vid , osv.
Skulle man approximera denna funktion från 0 till hade avståndet varit från origo till häften av , då ser det ut som området hade varit bergränsat av funktionen om man gör ett vertikalt sträck från .
Det stämmer. Men funktionen ”rör sig” 3 gånger så snabbt som .
Så du kommer integrera över en asymptot och det gör i detta fall att integralen blir divergent.
tomast80 skrev:Det stämmer. Men funktionen ”rör sig” 3 gånger så snabbt som .
Så du kommer integrera över en asymptot och det gör i detta fall att integralen blir divergent.
Precis, det förstår jag! Men betyder det att värdet på integralen blir oändlig?
Det stämmer! Det enklaste sättet att inse det är att beräkna följande gränsvärde, vilket motsvarar det Albiki skriver. Nöjer mig med den vänstra integralen:
Den primitiva funktionen är enkel att beräkna.
tomast80 skrev:Det stämmer! Det enklaste sättet att inse det är att beräkna följande gränsvärde, vilket motsvarar det Albiki skriver. Nöjer mig med den vänstra integralen:
Den primitiva funktionen är enkel att beräkna.
Stort tack!
Men F(x) till Tan(3x) är väl inte trivialt?!
Jo, ganska enkelt. Tips:
Ser du några likheter med:
?



