4
svar
100
visningar
Leonhart är nöjd med hjälpen
Trigonometrisk funktion
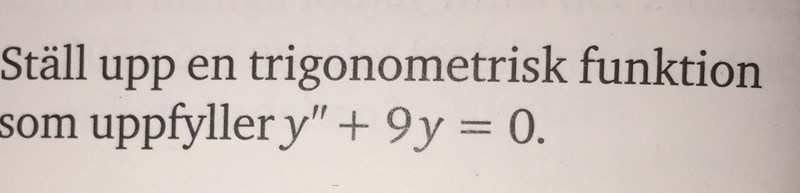
Jag gjorde såhär men det blir fel eftersom VL är ej lika med HL:
Hur kan man tänka för att få fram rätt svar?
Prova en lite generellare ansats. Kanske , eller .
eller y=ekx brukar funka på denna typ av ekvationer ...
joculator skrev:eller y=ekx brukar funka på denna typ av ekvationer ...
Nä, det står i uppgiftstexten att det skall vara en trigonometrisk funktion - annars skulle jag hålla med dig.
Om man löser med y=ekt får man 2 lösningar: k1=3i och k2=-3i.
Om vi hade haft de komplexa rötterna k1 =a+ib , k2 =a-ib hade vi haft den generella lösningen:
vilket med a=0 och b=3 ger oss
Alltså:
Du kan sedan välja vilka c1 och c2 som du vill.




