Tröghetsmoment
Hur ska man lösa andra delen av den här uppgiften?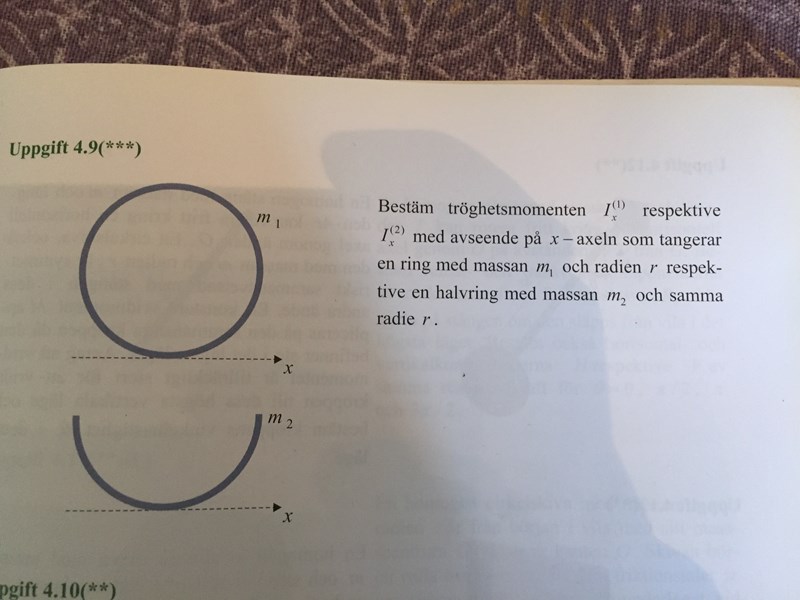
Jag lyckas få fram ett utryck för en väldigt svår integral att lösa, se nedan: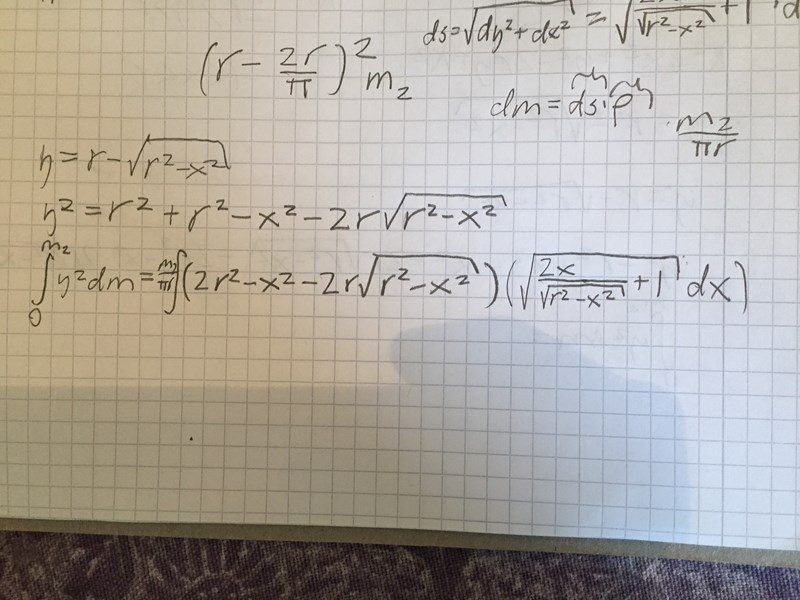
Skriv lösningen eller vilken annan metod jag bör använda för att lösa uppgiften, annars skriv inte alls. Tack!
Blir det lättare om du använder Steiners sats?
Det går att lösa helt utan integration.
Använd Dr. G:s ledning och tänk på att figuren är plan.
Dr. G skrev:Blir det lättare om du använder Steiners sats?
Jag tänkte på det, men hur bestäms i såna fall tröghetsmomentet kring halvcirkelbågens masscentrum?
Johanspeed skrev:Dr. G skrev:Blir det lättare om du använder Steiners sats?
Jag tänkte på det, men hur bestäms i såna fall tröghetsmomentet kring halvcirkelbågens masscentrum?
Vad blir tröghetsmomentet kring en axel som är längs en diameter till halvcirkelbågen?
PATENTERAMERA skrev:Johanspeed skrev:Dr. G skrev:Blir det lättare om du använder Steiners sats?
Jag tänkte på det, men hur bestäms i såna fall tröghetsmomentet kring halvcirkelbågens masscentrum?
Vad blir tröghetsmomentet kring en axel som är längs en diameter till halvcirkelbågen?
Det borde bli hälften av tröghetsmomentet kring en axel längs en diameter till cirkelbågen, den kan ju ses som uppbyggd av två halvcirkelbågar.
PATENTERAMERA skrev:PATENTERAMERA skrev:Johanspeed skrev:Dr. G skrev:Blir det lättare om du använder Steiners sats?
Jag tänkte på det, men hur bestäms i såna fall tröghetsmomentet kring halvcirkelbågens masscentrum?
Vad blir tröghetsmomentet kring en axel som är längs en diameter till halvcirkelbågen?
Det borde bli hälften av tröghetsmomentet kring en axel längs en diameter till cirkelbågen, den kan ju ses som uppbyggd av två halvcirkelbågar.
Om du menar det jag tror att du menar så blir det fel eftersom tröghetsmomentet från halvcirkelbågen närmast som tangerar x-axeln blir mindre än halvcirkel bågen längst bort. Det blir mycket lättare och går snabbare om du visar mha av beräkningar istället för att försöka förklara i ord
Johanspeed skrev:
Om du menar det jag tror att du menar så blir det fel eftersom tröghetsmomentet från halvcirkelbågen närmast som tangerar x-axeln blir mindre än halvcirkel bågen längst bort. Det blir mycket lättare och går snabbare om du visar mha av beräkningar istället för att försöka förklara i ord
Johanspeed, var inte så otacksam! Det är du som skall lösa dina uppgifter, inte någon annan. /moderator
Johanspeed skrev:PATENTERAMERA skrev:PATENTERAMERA skrev:Johanspeed skrev:Dr. G skrev:Blir det lättare om du använder Steiners sats?
Jag tänkte på det, men hur bestäms i såna fall tröghetsmomentet kring halvcirkelbågens masscentrum?
Vad blir tröghetsmomentet kring en axel som är längs en diameter till halvcirkelbågen?
Det borde bli hälften av tröghetsmomentet kring en axel längs en diameter till cirkelbågen, den kan ju ses som uppbyggd av två halvcirkelbågar.
Om du menar det jag tror att du menar så blir det fel eftersom tröghetsmomentet från halvcirkelbågen närmast som tangerar x-axeln blir mindre än halvcirkel bågen längst bort. Det blir mycket lättare och går snabbare om du visar mha av beräkningar istället för att försöka förklara i ord
Inte om du lägger axeln som en diameter till cirkelbågen.
Smaragdalena skrev:Johanspeed skrev:
Om du menar det jag tror att du menar så blir det fel eftersom tröghetsmomentet från halvcirkelbågen närmast som tangerar x-axeln blir mindre än halvcirkel bågen längst bort. Det blir mycket lättare och går snabbare om du visar mha av beräkningar istället för att försöka förklara i ordJohanspeed, var inte så otacksam! Det är du som skall lösa dina uppgifter, inte någon annan. /moderator
Som jag skrev i starten av tråden så är jag endast intresserad av lösningen, det är så jag lär mig lättast. Jag är inte otacksam, läs istället så förstår du. Jag vill föresten i framtiden att Smaragdalena inte skriver i några av mina startade trådar eftersom hon aldrig svarar efter det som frågas och heller inte brukar ge mig nya insikter. Istället skriver hon ibland sök på wikipedia, vilket jag självklart har gjort..
Johanspeed, om du bara vill ha färdiga lösningar är inte Pluggakuten rätt sajt för dig.
Som moderator är det min uppgift att uppmärksamma alla regelbrott som begås av dem som skriver här på Pluggakuten, alltså även i dina trådar.
Om du har sökt på Wikipedia bör du skriva det i din trådstart, så att vi som svarar här slipper kasta bort vår tid på att göra det som du redan har gjort. /moderator
Johanspeed skrev:Dr. G skrev:Blir det lättare om du använder Steiners sats?
Jag tänkte på det, men hur bestäms i såna fall tröghetsmomentet kring halvcirkelbågens masscentrum?
Tröghetsmomentet för halvcirkelbågen med avseende på diametern är hälften av tröghetsmomentet för en cirkel med avseende på diametern. Integrera eller slå upp.
Masscentrums y-koordinat för en halvcirkel kan du t.ex räkna ut med Pappus regel (integrera eller slå upp).
Steiners sats en gång ger då tröghetsmomentet m.a.p masscentrum.
Steiners sats en gång till ger då tröghetsmomentet m.a.p valfri axel.
Dr. G skrev:Johanspeed skrev:Dr. G skrev:Blir det lättare om du använder Steiners sats?
Jag tänkte på det, men hur bestäms i såna fall tröghetsmomentet kring halvcirkelbågens masscentrum?
Tröghetsmomentet för halvcirkelbågen med avseende på diametern är hälften av tröghetsmomentet för en cirkel med avseende på diametern. Integrera eller slå upp.
Masscentrums y-koordinat för en halvcirkel kan du t.ex räkna ut med Pappus regel (integrera eller slå upp).
Steiners sats en gång ger då tröghetsmomentet m.a.p masscentrum.
Steiners sats en gång till ger då tröghetsmomentet m.a.p valfri axel.
Kommer in (väldigt) sent här men har en fråga då jag fastnat på samma uppgift...
Eftersom parallellförflyttningssatsen är , när man då använder formeln "första" gången för att få ett tröghetsmoment m.a.p masscentrum, vilken axel ska man använda som ? Tänker att man skriver om den som och är osäker på vart man förflyttar tröghetsmomentet från, vad ska då även vara?
Har fått för mig sedan tidigare att tröghetsmomentet (säg, för en stel kropp i x-y-planet då z=0) redan beräknas m.a.p masscentrum då man beräknar . Tror egentligen jag har problem med att visualisera vart på en (2D) kropp tröghetsmomentet verkar, du råkar inte ha några tips?



