Två trianglar

Det går ju alltid att använda bondmetoden och anta $y=kx+m$ och använda omkretserna och punkten $(3,6)$ för att sedan få ett ekvationssystem i k och m. Dock blir det ganska fula ekvationer..

AlvinB skrev:

Det går ju alltid att använda bondmetoden och anta $y=kx+m$ och använda omkretserna och punkten $(3,6)$ för att sedan få ett ekvationssystem i k och m. Dock blir det ganska fula ekvationer..

 Precis! De är inte så roliga att tas med. Tricket är att välja rätt variabel att lösa ut.

Jag tycker ändå mina ekvationer blir fruktansvärt fula..

$\sqrt{9+(m-6)^2}+m=-\frac{m}{k}+\sqrt{36+(3+\frac{m}{k})^2}$

$3k+m=6$

Hursomhelst får jag ekvationen till

$y=-{\displaystyle \frac{4}{3}}x+10$

Snyggt! Det är helt rätt! 👏

Ja, den ekvationen är inte så lätthanterlig.

Ett alternativ är att kalla den övre vinkeln i den stora triangeln för $v$. Då kan man uttrycka trianglarnas sidlängder genom olika samband med denna vinkel. Blir dock inte helt smidig ekvation där heller...

Kommer så här långt med ”vinkelmetoden”. Dock blir den slutliga ekvationen att lösa rätt knölig. Nån som har några bra idéer hur den ska lösas?

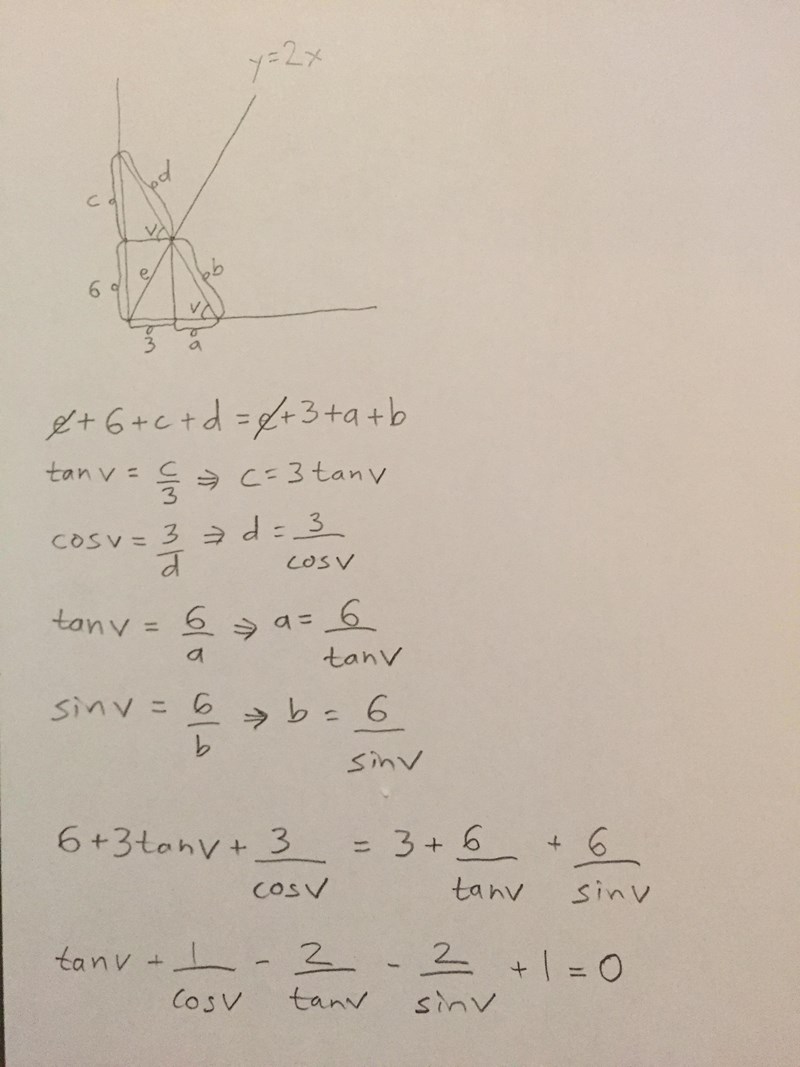
Oj Tomas det här blev sommarens utmaning!
Ett försök till lösning kommer här, men tyvärr lyckades jag inte att helt gå i mål.

Givna uppgifter är:
Vi har en rät linje . Den går igenom punkten $(3;6)$
En rät linje med negativ lutning ska ritas in som också skär punkten (3;6)
På det viset finns en triangel med basen på x-axeln och en triangel med basen på y-axeln om vi låter$x\ge 0$ och $y\ge 0$

Frågan lyder:
Vad blir ekvationen för linjen med den negativa lutningen för att de två trianglarna ska ha samma omkrets.

Angreppsmetod:
Vi försöker att ta reda på vilket värde $k$ ska ha för att den nya räta linjen $y=kx+m$ ska ha rätt lutning så att de två trianglarna får lika stor omkrets.

Först ritar vi en figur

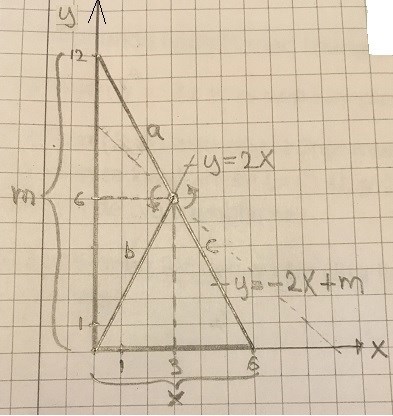
Här är också linjen $y=-2x+m$ inritad för att kunna bilda oss en uppfattning om hur det kommer att se ut.
Att just värdet $k=-2$ valdes, var endast för att ha något att börja med.
Som vi ser så kommer den nya räta linjens m-värde att direkt motsvara y-värdet. Därför är basen på triangeln mot y-axeln lika med m-värdet. Sidorna på den triangeln är namngivna med a och b.
Basen på triangeln mot x-axeln motsvaras av x-värdet. Sidorna på den triangeln är namngivna med b och c.
De två pilarna som är inritade anger att den nya räta linjen har sitt rotationscentrum i punkten (3;6) som synes så är rotationen begränsad om vi fortfarande ska få två trianglar med angivna villkor.

Om vi nu tittar på omkretsarna så är de för triangel T1 = m+a+c och för triangel T2 = x+b+c
Eftersom omkretsen ska vara lika stor för bägge trianglarna så kan vi sätta att
T1 =T2 vilket medför att m+a+b = x+b+c
b går att förkorta bort och det syns i figuren att den är lika för bägge trianglarna och påverkas inte av den nya räta linjens lutning.
Så vi har att m+a = x+c

Vi kan nu mäta med linjal för att se hur nära vi kommit.
$m+a\approx 18,6 l.e$
$x+c\approx 12,8 l.e.$

För att få något att jämföra med så ritar vi in linjen $y=-1x+m$
Den syns lite svagt i figuren och börjar där m=9 och slutar vid x=9.
Vi mäter igen och får:
$m+a\approx 13,1 l.e.$
$x+c\approx 17,4 l.e.$

OK då ser vi att vår lösning bör ligga mellan $k=-2$ och $k=-1$
Vi vet då också att vårt intervall blir inom $6<x<9$

Nu är det dags att ta fram några formler.
Vi tittar först på $k$ som en funktion av $x$.

$k=\frac{y_2-y_1}{x_2-x_1}$  Om vi utgår från punkten $(3;6)$ och väljer nästa punkt på x-axeln $(x;0)$  då får vi lutningen $k$ för vår negativt lutande linje.

Då får vi att $k=\frac{0-6}{x-3}$   dvs.
 $\mathit{k}\mathbf{\left(}\mathit{x}\mathbf{\right)}\mathbf{=}\mathbf{-}\frac{\mathbf{6}}{\mathbf{x}\mathbf{-}\mathbf{3}}$

Nu kan vi välja värdet på x inom intervallet $6<x<9$ och få fram värdet på $k$.

Sedan behöver vi en formel för $m\left(k\right)$ dvs. $m$ som en funktion av $k$.

Vi använder $k=\frac{y_2-y_1}{x_2-x_1}$ igen för punkterna $(0;m)$ och $(3;6)$

Då får vi att $k=\frac{6-m}{3-0}$   och $k=\frac{6-m}{3}$   det kan vi skriva som $3k=6-m$ och $m=6-3k$  och då har vi
$\mathit{m}\mathbf{\left(}\mathit{k}\mathbf{\right)}\mathbf{=}\mathbf{6}\mathbf{-}\mathbf{3}\mathit{k}$  

En formel för $a\left(k\right)$ behöver vi också. Där kan vi använda pythagoras sats.
$a$ är hypotenusan och $3$ (x-riktning) är en katet och en katet är $m-6$.

Så  $a^2=3^2+(m-6{)}^2$ medför att vi får $a=\sqrt{9+\left(\right(6-3k)-6{)}^2}$ 
Obs. att $m$ ersattes med $(6-3k)$
Nu kan vi skriva $a=\sqrt{9+(-3k{)}^2}$  och  $a=\sqrt{9+9k^2}$

$\mathit{a}\mathbf{\left(}\mathit{k}\mathbf{\right)}\mathbf{=}\mathbf{3}\sqrt{\mathbf{1}\mathbf{+}{\mathbf{k}}^{\mathbf{2}}}$  

Slutligen behöver vi en formel för kateten $c$ också.

Även till den kan vi använda pythagoras sats.

 $c^2=(x-3{)}^2+6^2$  eftersom vi känner till $x$ så kan vi använda $c\left(x\right)$

 $\mathit{c}\mathbf{\left(}\mathit{x}\mathbf{\right)}\mathbf{=}\sqrt{\mathbf{(}\mathbf{x}\mathbf{-}\mathbf{3}{\mathbf{)}}^{\mathbf{2}}\mathbf{+}\mathbf{36}}$
 

Nu kan vi göra en tabell, där vi använder oss av att vi känner till att 6 < x < 9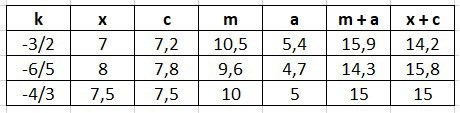

Första raden med x = 7 visar att m + a blir större än x + c
Andra raden med x = 8 visar att m + a blir mindre än x + c
Tredje raden med x = 7,5 visar att m + a blir lika med x + c

Närmare än så här kom jag inte. Jag hade hoppats på att finna en lösning och har suttit med alla möjliga ekvationer, men stupat på att jag inte kom ifrån pythagoras sats och en massa invecklade ekvationer. Precis som Tomas och Alvin konstaterat.

Kanske det kan finnas någon liten fingervisning i svaret att x och c blev lika stora samt förhållandet m / a blir 2, men jag har inte lyckats hitta en bra förklaring.

Svaret på Tomas fråga blir precis som Alvin konstaterat $y=-\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.x +10$ 

Snyggt ConnyN! Mycket gedigen genomgång av uppgiften! 👏

Jag funderar likadant som du: finns det någon genväg för att lösa detta på något mer smidigt sätt? 🤔

Hoppas att någon av de skarpaste hjärnorna här på PA tar sig an detta problem så får vi kanske svaret! ✊️

Jag väntar...

En ytterligare studie visade att så länge vi förflyttade oss längs med linjen $y=2x$ så håller resonemanget att $x$ och $c$ kommer att vara lika stora och att förhållandet $\frac{m}{a}=2$ 
Linjerna med negativ lutning har samma $k$ för alla punkter längs $y=2x$ och är sålunda parallella.

Däremot vid prov med en linje $y=1,25x$ och en punkt $(4 ; 5)$ så visade det sig att vi får ett annat förhållande för att få samma omkrets på de två trianglarna.

Vi har nu försökt att hålla oss till matte 2, men om vi tillåter högre matematik finns det då någon tänkbar algebraisk lösning?

Hej!

Den sökta räta linjen går genom punkterna $(3,6)$ och $(3+a,0)$.

Det gäller att finna $a$ som gör de två nämnda trianglarnas omkretser lika stora.

Att ange linjens ekvation ($y=6+\frac{6}{-a}(x-3)$) är en bisak när man väl känner talet $a$.

Albiki skrev:

Hej!

Den sökta räta linjen går genom punkterna $(3,6)$ och $(3+a,0)$.

Det gäller att finna $a$ som gör de två nämnda trianglarnas omkretser lika stora.

Att ange linjens ekvation ($y=6+\frac{6}{-a}(x-3)$) är en bisak när man väl känner talet $a$.

 Triangel A har omkretsen

    $\displaystyle(3+a)+\sqrt{3^2+6^2}+b(a).$

Triangel B har omkretsen

    $\displaystyle \sqrt{3^2+6^2}+6+c(a)+d(a)$,

där likformighet ger $a \cdot c(a)=6 \cdot 3$ och $a \cdot d(a)=3 \cdot b(a)$. Triangel A har samma omkrets som triangel B precis då

    $\displaystyle a + b(a) = 3+c(a) + d(a) \quad\Leftrightarrow\quad a+b(a)=3+\frac{18}{a}+\frac{3b(a)}{a}.$

Pythagoras sats ger att $b(a) = \sqrt{6^2+a^2}$, vilket ger en ekvation som det positiva talet $a$ måste uppfylla för att de två trianglarnas omkretsar ska vara lika.

    $\displaystyle a+\sqrt{36+a^2}=3+\frac{18}{a}+\frac{3\sqrt{36+a^2}}{a}.$

Ekvationen som ska lösas kan uttryckas i variabeln $\xi=\frac{6}{a}$.

    $\displaystyle\frac{\xi}{2}\sqrt{1+\xi^2}=1+\frac{\xi}{2}+\sqrt{1+\xi^2}\quad\Leftrightarrow\quad (1-\frac{\xi}{2})(1-\sqrt{1+\xi^2}) = 2.$

En bild av funktionen $f(x) = (1-\frac{x}{2})(1-\sqrt{1+x^2}) - 2$ i Desmos indikerar att den har ett nollställe när $x \approx 3,51$ vilket motsvarar

    $\displaystyle a \approx \frac{6}{3,51} \approx 1,71.$

Det går bra för mig att hänga med på vad du skriver Albiki till det här sista. Att variabel$\xi =\frac{6}{a}$ är OK och ekvationen du får fram verkar vettigt. Jag har inte kontrollräknat den, men svaret du tar fram är konstigt.

$x\approx 3,51 och a\approx 1,71$vad använder du den informationen till?

I min värld är $a=4,5$, men vi kanske talar om helt olika saker?

 Jag har nu provat att sätta in $\xi =\frac{6}{a}$ vilket innebär att $a$ ska ersättas med $a=\frac{6}{\xi }$

Det gör att jag kommer till $\frac{2}{\xi }(1+\sqrt{1+{\xi }^2})=1+\xi +\sqrt{1+{\xi }^2}$

Inte riktigt lika ditt, men nära. Vad tror du Albiki?

För att testa satte jag in att $\xi =\frac{6}{a}$ och ersatte $a$ med $4,5$ och det ser ut att stämma, så ekvationerna är nog rätt nu.
Fast jag hade aldrig kommit på detta utan din hjälp Albiki. Det har varit fantastisk roligt att få vara med på den här resan så här långt.
Är det kört nu? Kommer vi inte längre?

En fråga som kvarstår är ju hur man löser ekvationerna analytiskt, d.v.s. utan numerisk eller grafisk lösning. Är det möjligt eller alltför krångligt? 🤔

Både min och Albikis ekvationer är lösliga algebraiskt. Man får en av rötterna ensam i ett led och kvadrerar sedan båda led. Då blir man kvar med endast en rot i det andra ledet. Man kan isolera den och kvadrera för att få ett polynom. Processen är inte sådär jätterolig att tugga sig igenom, men för Albikis ekvation är den hyfsat dräglig. Jag löste min ekvation för hand, men det blev en sjuhelvetes massa beräkningar..

AlvinB skrev:

Både min och Albikis ekvationer är lösliga algebraiskt. Man får en av rötterna ensam i ett led och kvadrerar sedan båda led. Då blir man kvar med endast en rot i det andra ledet. Man kan isolera den och kvadrera för att få ett polynom. Processen är inte sådär jätterolig att tugga sig igenom, men för Albikis ekvation är den hyfsat dräglig. Jag löste min ekvation för hand, men det blev en sjuhelvetes massa beräkningar..

 Snyggt! 👌 Verkar inte finnas några enkla genvägar här alltså...

Hej!

Ekvationen

    $\displaystyle a+\sqrt{36+a^2}=3+\frac{18}{a}+\frac{3\sqrt{36+a^2}}{a}$

kan skrivas

    $\displaystyle a^2-3a-18 = (3-a)\sqrt{36+a^2} \quad\Leftrightarrow\quad (a+3)(a-6)=(3-a)\sqrt{36+a^2} \quad\Rightarrow\quad (\frac{(a+3)(6-a)}{a-3})^2 = 36+a^2.$

Denna ekvation kan förenklas betydligt till andragradsekvationen

    $\displaystyle 9a(36-8a)=0$

vars enda tillåtna lösning är $a = \frac{9}{2}.$

Kontroll: Om $a = \frac{9}{2}$ så är

    $\displaystyle 3+\frac{18}{a}+\frac{3\sqrt{36+a^2}}{a} = 3+4+\frac{6}{9}\cdot\frac{15}{2}=7+5=12$

och

    $\displaystyle a+\sqrt{36+a^2} = \frac{9}{2} + \frac{15}{2}=\frac{24}{2} = 12.$

Wow, man bugar sig.