Tycker ni att dQ=TdS för en allmän, kvasistatisk process?
Halloj!
Jag har nyligen fått reda på att det finns de som anser att differentialsambandet håller för alla kvasistatiska processer. En kvasistatisk process defineras som en process under vilken det aktuella systemet ständigt befinner sig i termodynamisk jämvikt; det är alltså en tät följd av jämviktstillstånd. Ett annat sätt att se det på är att processen definierar en sammanhängande kurva längs hyperytan som definieras av entropin i systemets konfigurationsrum (det rum som spänns upp av systemets extensiva koordinater under förutsättningen att systemet befinner sig i jämvikt). Jag är nyfiken på vad ni tycker och hur ni i så fall även skulle motivera er åsikt. Tycker ni att gäller allmänt för en sådan process eller inte?
Jag har ett exempel som jag anser visar att sambandet inte gäller för alla kvasistatiska processer. Låt oss antaga att vi har en ideal gas instängd i en adiabatisk, ogenomsläpplig och rigid behållare där vi instantant kan förändra volymen genom att förlytta en kolv. Se figur nedan:
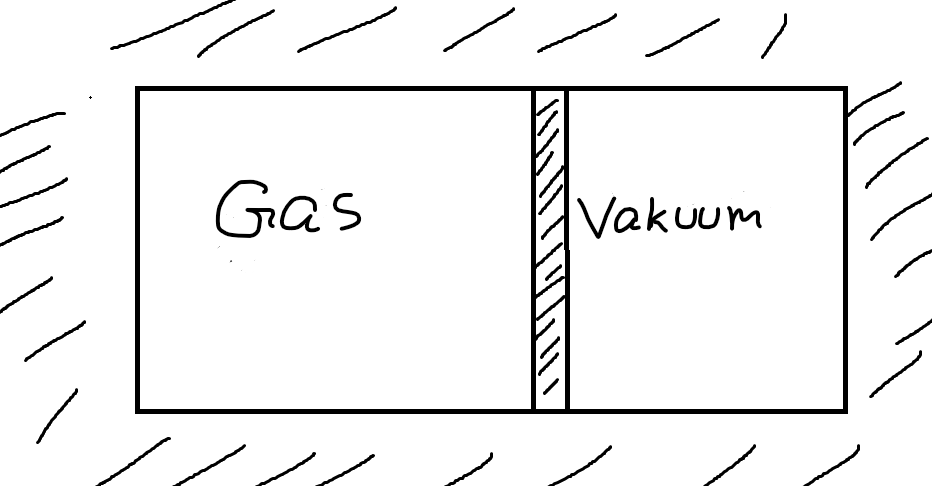
Vi kan tänka oss att vi flyttar kolven instant en bit åt höger till en slutvolym . Då kommer gasen turbulent expandera mot det vakuum som blottas och till slut kommer en ny jämvikt inrätta sig. Låt säga att vi nu istället låter gasen expandera kvasistatiskt mot vakuum till samma slutvolym . Då gäller:
Integrerar vi detta mellan två volymer (där slutvolymen är större än startvolymen) kommer vi alltid ha men samtidigt .
Vad tycker ni "-are" om detta?
dQ=TdS gäller för reversibla processer, men exemplet du beskrev är irreversibel.
Jag är i samma läger som du! Den beskrivna processen är internt irreversibel men kvasistatisk. Detta är anledningen till att jag blev så förvånad när jag såg att de fanns de som svär vid att denna process inte är kvasistatisk eftersom inte gäller. Faktum är att en författare jag såg till och med definierade den här processen som icke-kvasistatisk eftersom han inte gillade att .
Ett djupt kaninhål, det här!


