Uppgift om rotationsvolym
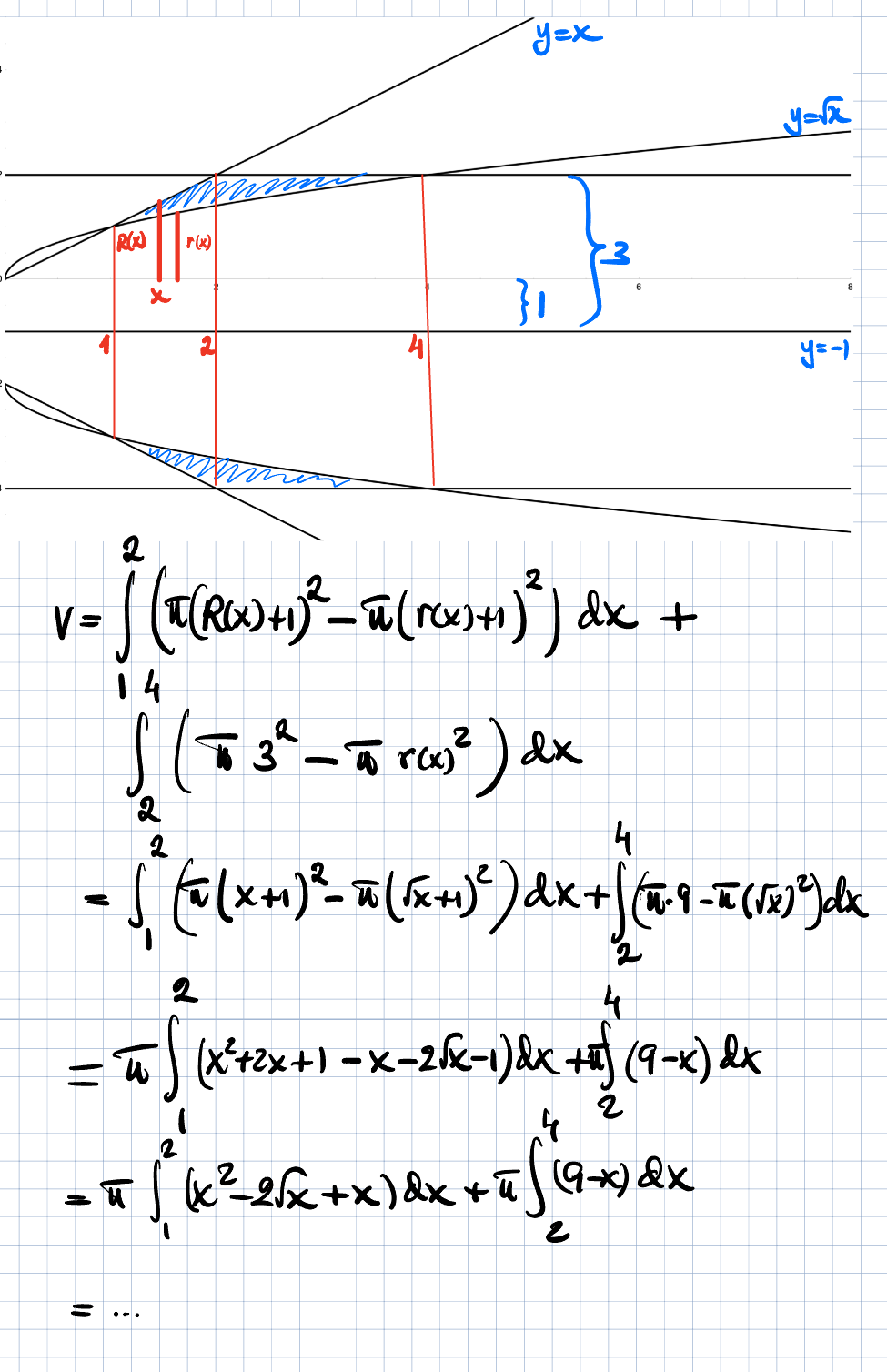
Hej! Har en uppgift där jag ska lösa vad rotationsvolymen blir när arean som är omringad av de tre funktionerna roterar kring x-axeln. Försöker använda skalmetoden men kommer inte fram till det rätta svaret av 14,1. Får fram uttrycket i nedre bilden men blir inte rätt :(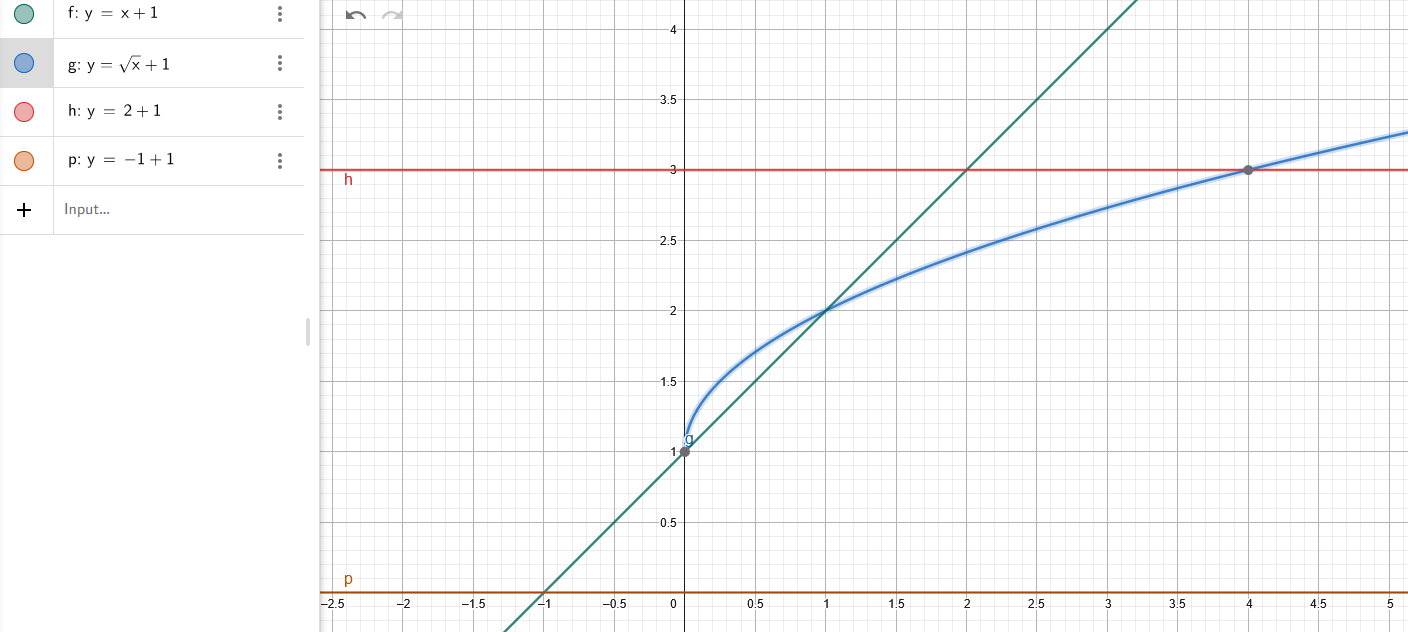
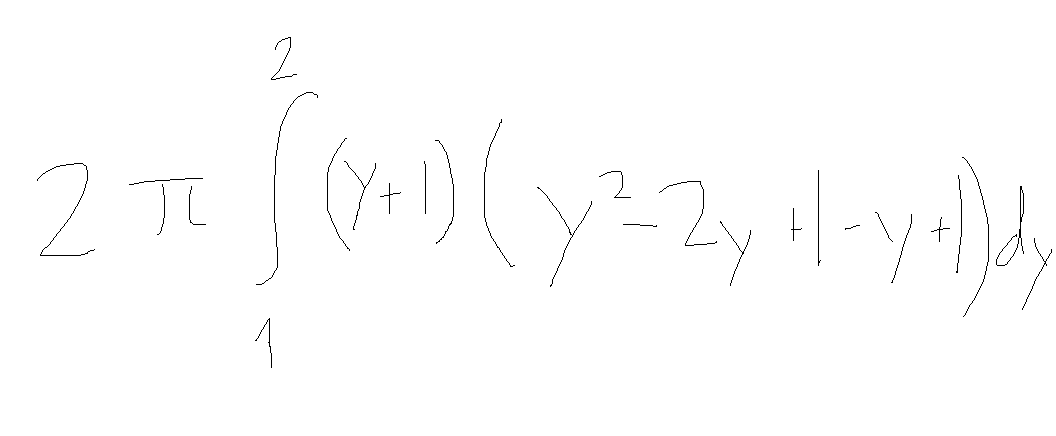
Kan du ta en bild på uppgiften?
Trinity2 skrev:Kan du ta en bild på uppgiften?
Den orginella uppgiften är så här, när jag använder skalmetoden här kunde jag eventuellt lösa uppgiften, men förstår inte riktigt vad som går fel när jag kör +1 på allt för att få rotationen ske runt x-axeln
Prova detta. Jag tror jag skrivit rätt
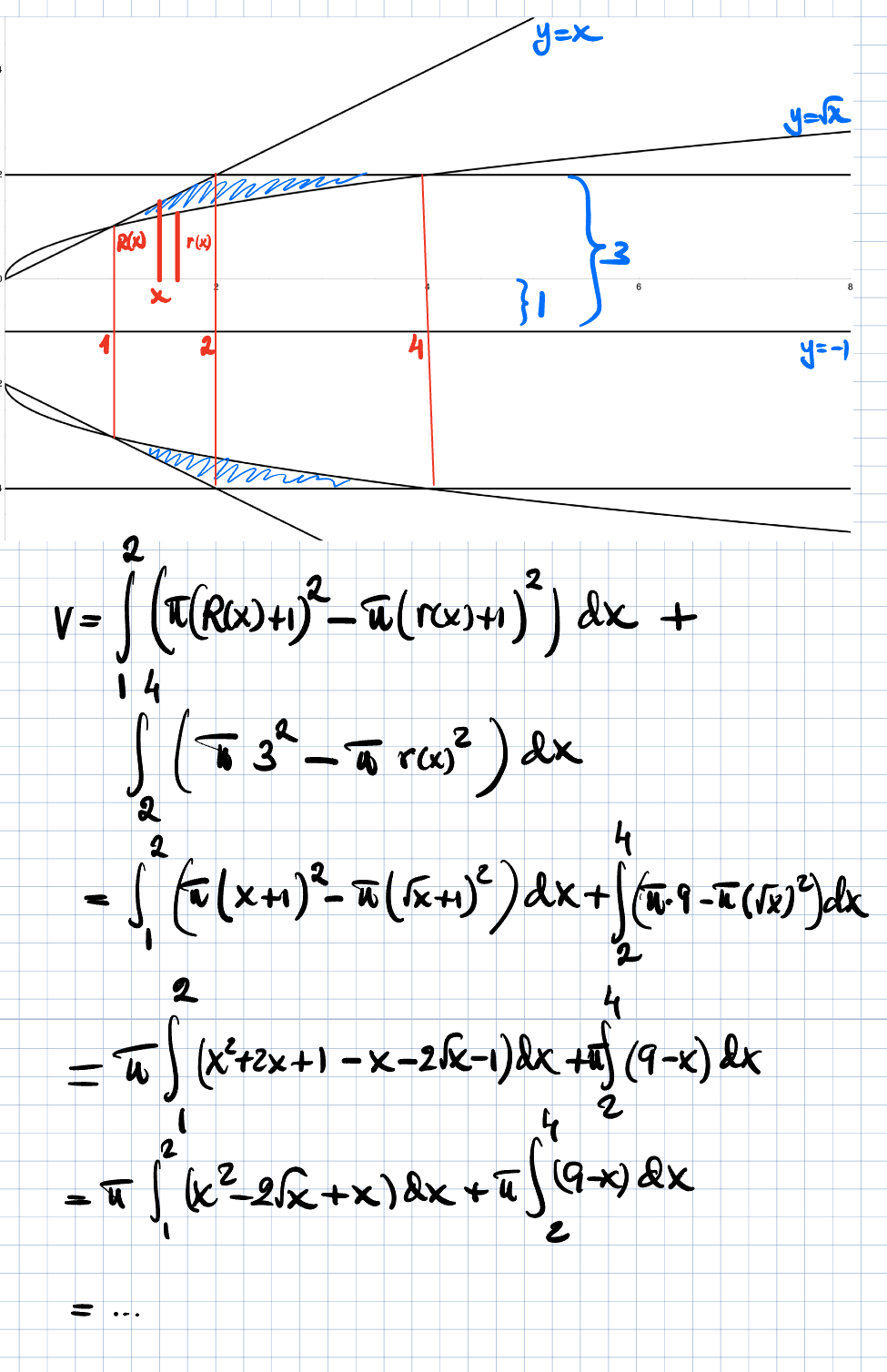
Trinity2 skrev:Prova detta. Jag tror jag skrivit rätt
Hej! Förlåt för sent svar!
Det här verkar fungera! Undrar bara om det på något sätt skulle kunna funka med skalmetoden när man också höjer allt med 1? är ganska nyfiken över det jag gör fel
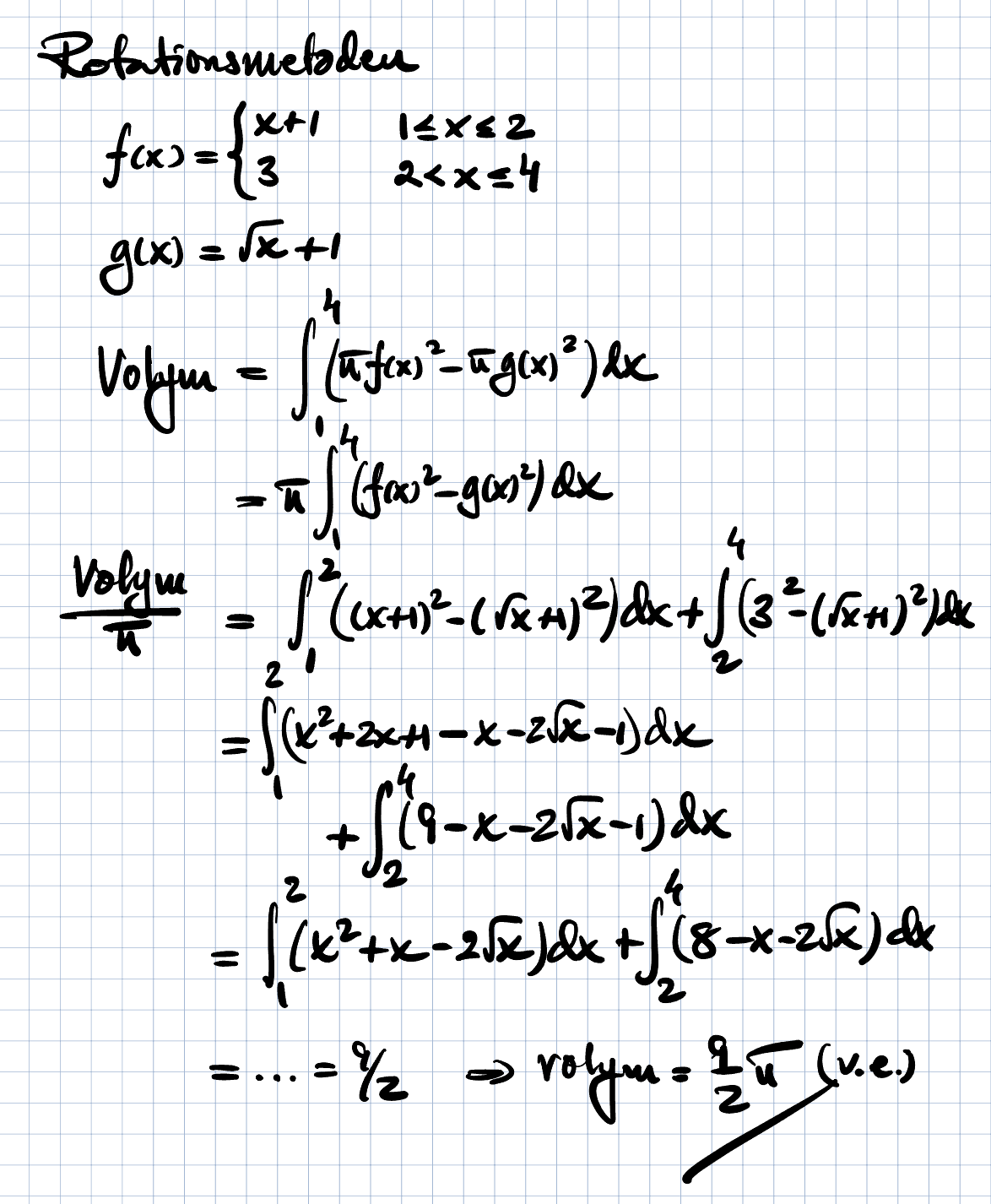
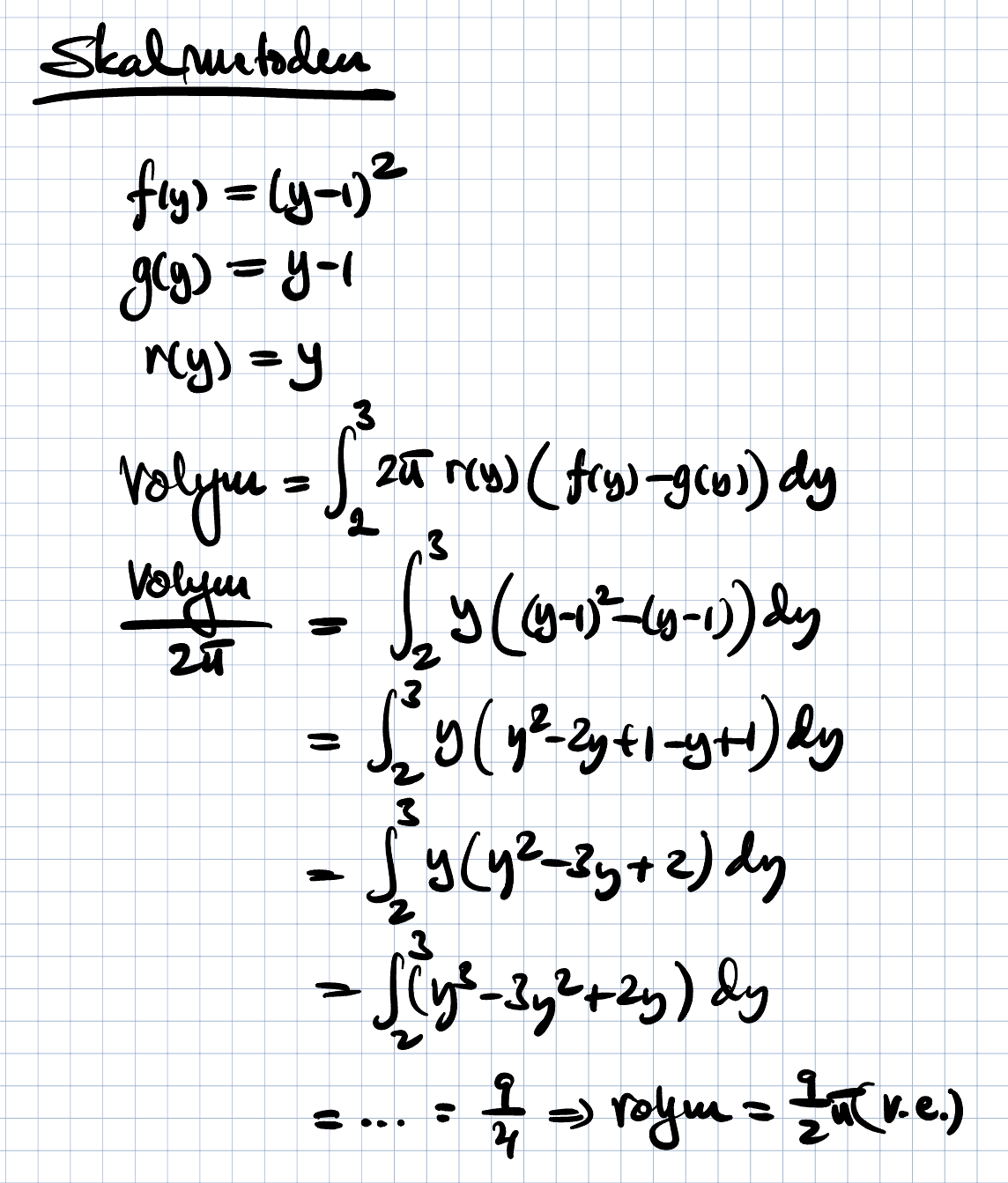 Glöm min förra uppställning, den har slarvfel i sig.
Glöm min förra uppställning, den har slarvfel i sig.
Här är ett mer heuristiskt resonemang utan förberedda formler:
Dela upp området parallellt med -axeln i pseudorektanglar med infinitesimal höjd . Varje sådan pseudorektangel har då bredd . Om en sådan pseudorektangel roteras runt erhålls en pseudoring. Omkretsen på denna ges då ungefär av . Ett volymelement ges då med infinitesimalt fel av . Integrera för att få den sammanlagda volymen:
Tillägg: 21 nov 2025 23:47
Jag använder begrepp som "pseudo" och "infinitesimala fel" men du kan lika gärna tänka bort detta. Då man integrerar i icke-standardanalys (vilket är det jag heuristiskt åberopar här) tar man något som kallas för standarddelen av en hyperfinit Riemannsumma och då dör de infinitesimala felen. Integralen i icke-standardanalys är ekvivalent med de typiska integraldefinitionerna som t.ex. suprema och infima av Darbouxsummor eller gränsvärden av finita Riemannsummor.