Utmaning: bestäm om tan(pi/7) eller sin(pi/4) är störst

Det är ganska jobbigt att rita en tangensgraf, men det råkar ju vara så att derivatan till tangensfunktionen är känd och enkel att rita i det relevanta intervallet. Och detsamma gäller för derivatan till sinusfunktionen. Så vi börjar med det:

$\displaystyle \frac{\mathrm{d}}{\mathrm{d}x} \tan x = \sec^2x$

$\displaystyle \frac{\mathrm{d}}{\mathrm{d}x} \sin x = \cos x$.

Om man skulle integrera dessa funktioner från och med noll till och med respektive värde får vi ju faktiskt samma sak som från början. Men det är ett sätt att representera värdena som areor istället. Så då skissar man helt enkelt grafen snabbt:

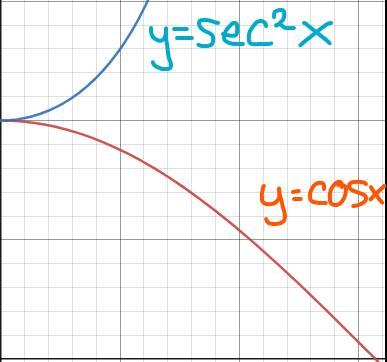
Sedan ritar vi dessutom in våra gränser:

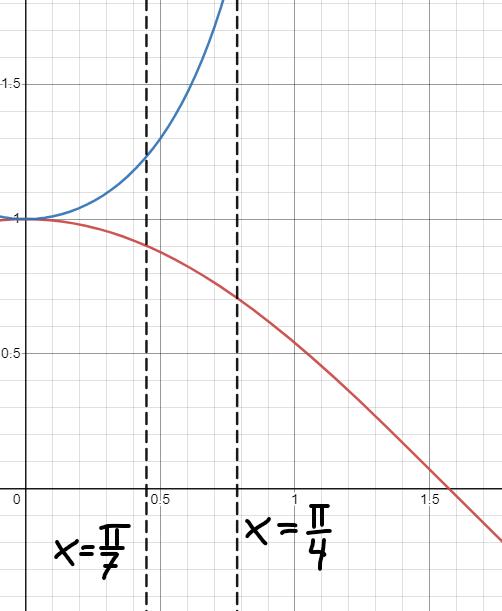
Om vi nu betraktar följande integraler:

$\displaystyle \int_{0}^{\pi/7}\frac{1}{\cos^2x}\mathrm{d}x$

$\displaystyle \int_{0}^{\pi/4}\cos x\;\mathrm{d}x$

Ser vi att den understa är betydligt större än den övre:

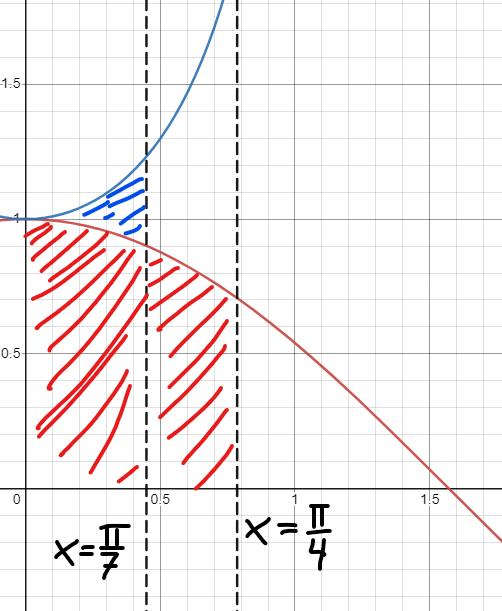
Den första delen av sina areor delar båda funktionerna men delen mellan $x=\frac{\pi}{7}$ och $x=\frac{\pi}{4}$ är betydligt större än det lilla blåa området. Således gäller att:

$\displaystyle \int_{0}^{\pi/4}\cos x\;\mathrm{d}x>\int_{0}^{\pi/7}\frac{1}{\cos^2x}\mathrm{d}x$

$\displaystyle \Rightarrow \sin{\frac{\pi}{4}}>\tan{\frac{\pi}{7}}$