Utverdera integralen 3pi/2 till -pi/2 för f(x) dx
Tror jag har tolkat rätt? Dock vet jag inte hur jag räknar ut en integral med sin^11(x)??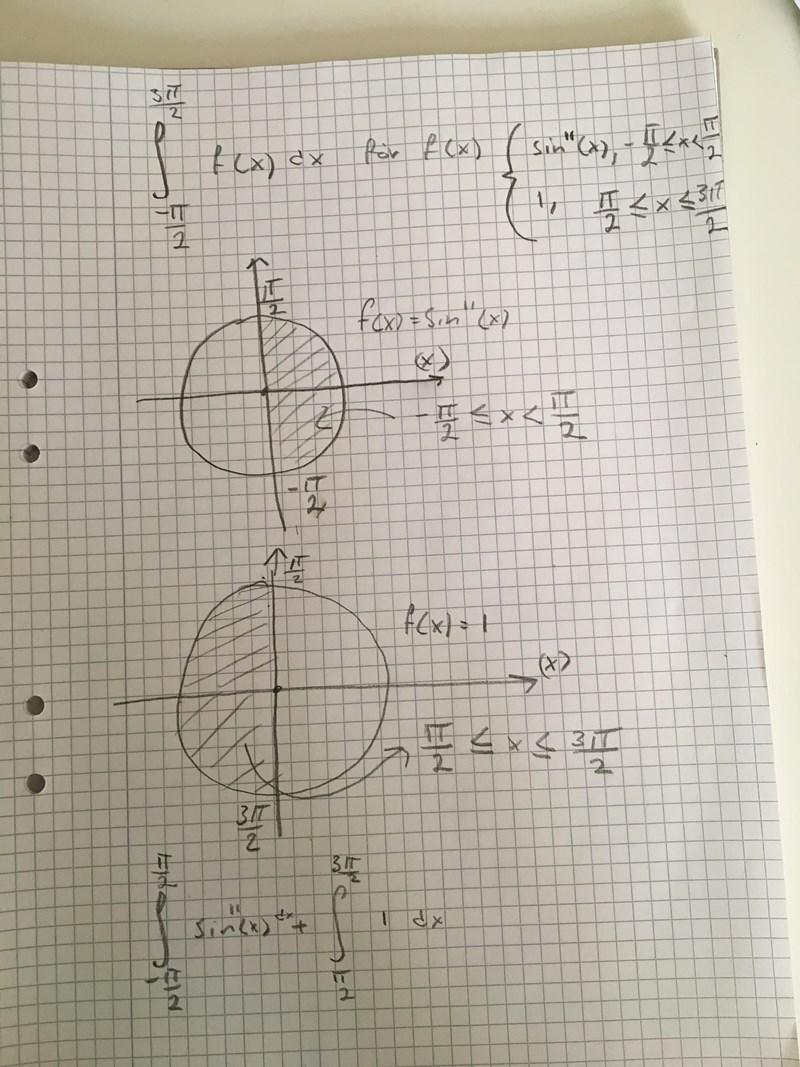
Är udda eller jämn eller nåt sånt?
sin11(x) är en udda funktion, dvs sin11(x) = -sin11(-x). Kan det vara någon hjälp?
Antiderivatan på sin(x) är ju - cos(x) men på sin^11(x) är det då -cos^11(x)? Då cos(-x) är väl samma som -cos(x).
Om man gör om det till -sin^11(-x) och tar primitiv funktion blir det då +cos^11(-x) = -cos^11(x), gud vad jag känner att allt jag skrev är gissningar...
Om f är en udda funktion så gäller det att
Kan du visa det?
Det kan jag ej visa tyvärr.
Jag vet inte varför det blir noll egentligen när man delar upp integralen i 2 delar men så verkar det bli.
när man delar upp integralen i 2 delar men så verkar det bli.
Nja, du verkar integrera f(x) = 1, det är ingen udda funktion. Men integralen blir noll, då sin11(x) är en udda funktion.
Okej, börjar fatta lite om udda och jämna funktioner, så den är noll eftersom den är udda, av det som är kvar är en integral f(x) =1dx kvar och då blir den 3pi/2 -2pi/2 = pi.
Ja, så borde det bli.
Ja det är rätt svar enl L.F.
Tack så mycket för hjälpen!


