Vad är det som gör att rosten säger "nej tack" till elektroner om spänningen är för låg?

Elektrodpotentialen är direkt relaterad till Gibbs energi via sambandet $\Delta G=-nFE$. En för låg potential innebär helt enkelt att ändringen i Gibbs energi är >0 och reaktionen blir icke-spontan. Att Delta G>0 innebär i förlängningen att processen inte leder till någon ökning av universums entropi och därför är den förbjuden enligt termodynamikens andra huvudsats.

Jag kanske inte var tydlig i min fråga.

Gibbs fria energi är ju en global egenskap som berör hela systemet, och det är spänning också - so far so good. Men när elektronerna väl når det mottagande speciet, hur kan det veta att "nej, om elektronen hade fullföljt hela sin bana hade den inte förlorat tillräckligt med energi så därför tackar jag nej"? Elektronmottagandet sker ju lokalt.

Förhoppningsvis framgick min fråga lite bättre. Givetvis vet jag att det mottagande speciet inte "vet" något alls på samma sätt som ingen atom "vill" uppfylla oktetregeln, men jag vet inte riktigt hur annars jag ska uttrycka mig.

Man kan inte se på reduktionen som ett separat steg utan det är en del av ett större system. Enklast är kanske attt först tänka sig en vanlig redoxreaktion, där det alltid måste finnas något som avger elektroner för att något annat ska kunna ta upp elektroner. Det är ganska lättförståeligt att denna typ av utbyte sker när partiklarna kommer nära varandra, kolliderar etc. En elektrokemisk cell fungerar på liknande sätt, med skillnaden att oxidation och reduktion är särade men fortfarande sammanbundna via ledningen där utbytet av elektroner kan ske.

Du kan alltså inte tänka att "nu kom en elektron hit, sedan åker den dit". Alla delsteg sker samtidigt.

Men det måste väl ändå gå att tala om vad som händer vid de enskilda halvcellerna?

Till skillnad från en vanlig redoxreaktion är det väl i detta fall inte samma elektroner som ingår i båda halvcellsreaktionerna samtidigt, även om det sker både reduktion och oxidation samtidigt?

Jodå, man kan bryta ner problemet i halvceller för att göra det mer lätthanterligt. Du har rätt i att det inte är samma elektroner som tas upp/avges vid reduktion och oxidation, men elektronerna är identiska så det har ingen direkt betydelse.

Men om det inte är samma elektroner som tas upp/avges under samma tidpunkt vid elektroderna, varför kan man inte följa en elektrons resa genom cellen och tänka "nu kom en elektron hit, sedan åker den dit"?

Det låter som en motsägelse? Varför följa en elektrons resa om det inte är någon elektron som reser?

Men det är väl elektroner som reser i kretsen, om än otroligt långsamt? Hur annars flödar elektronerna i kretsen? Jag menar, det är ju inte så att halvcellerna "känner av varandra". Reaktionen drivs eftersom det råkar fortsätta ske oxidation vid anoden.

Om vi hade försökt driva cellen utan en anod hade vi väl också fått ett elektronflöde under några nano- eller millisekunder, tills laddningsgradienten mellan batteriets anod och den elektrolytiska cellens katod leder till ett E-fält som är motriktat den önskade riktningen. Om spänningen inte hade varit "tillräckligt hög" här, hade vi fått någon reduktion under denna jättekorta tid?

I princip är det så att halvcellsreaktionerna äger rum oberoende av varandra, men laddningsseparationen som uppstår motverkar detta ganska direkt. 

Så låt säga, rent principiellt, att vi helt enkelt struntar i anodreaktionen och endast studerar katodreaktionen. Då har vi, om vi tar reduktion av rost som exempel:

$\displaystyle \mathrm{FeO(OH)(s)+3H^+ (aq)+3e^-\longrightarrow Fe(s)+2H_2O (l)}$

Vi kan även här beräkna en reduktionspotential, låt säga att den är $\varepsilon^\ominus = -5 \;\mathrm{V}$ för enkelhetens skull.

Om vi då skulle göra följande uppkoppling, där jag explicit har ritat ut spänningskällan:

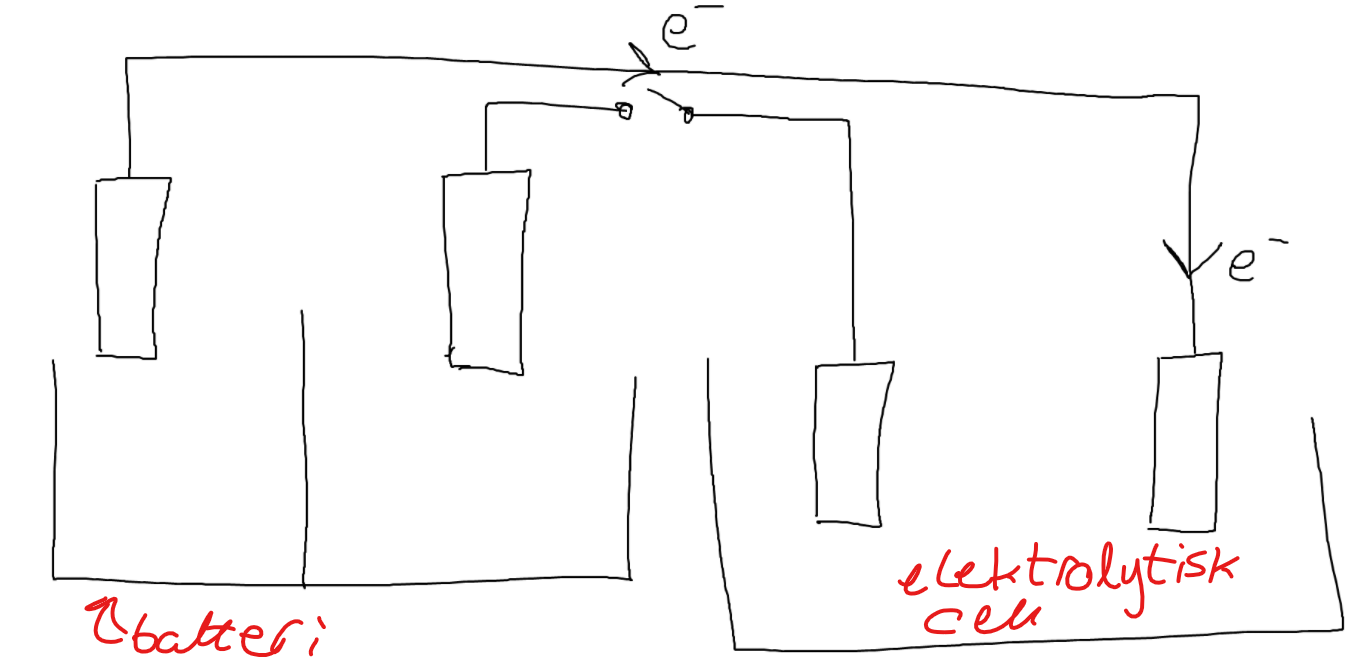
Skulle någon reduktion ske under denna nästan infinitesimalt korta tidsperiod om batteriet i sig har en spänning som ligger under 5 V? Det som verkar så märkligt är att katoden i den elektrolytiska cellen på något sätt kan känna av hur mycket energi varje laddningsenhet skulle förlora på en "hel resa" genom cellen, förutsatt att min tolkning av vad spänning är är rätt. Liksom varför spelar det ens någon roll för de enskilda halvcellerna hur mycket energi varje laddningsenhet skulle förlora på en hel vandring i cellen? När de når halvcellerna har de ju inte tagit sig genom hela kretsen, och energin de förlorar blir ju i stort sett bara värme.

I det där fallet är katoden i den elektrolytiska cellen kopplad till anoden hos batteriet, så huruvida reduktionen vid katoden kan äga rum beror på reaktionen som sker vid anoden. Om ämnet vid anoden i batteriet är mindre lättoxiderat än ämnet vid katoden i elektrolyscellen är lättreducerat får du ingen ström. Dessa två processer är sammankopplade, de går inte att betrakta separat.

Men om vi sluter kretsen, alltså sluter ledaren mellan batteriets katod och den elektrolytiska cellens anod, har vi inte samma problem då? Att det som avgör huruvida reduktionen kan ske i den elektrolytiska cellen är hur lättreducerat ämnet vid katoden i elektrolyscellen är jämfört med hur lättoxiderat ämnet vid anoden i batteriet är? (dvs. inte batteriets spänning)

Det jag försökte rita upp var det allmäna fallet av hur man driver en elektrolytisk cell med ett batteri men det kanske inte var så allmänt som jag trodde...? Jag utgick från den här bilden där man gjorde typ smältelektrolys, alltså med inerta elektroder i elektrolyscellen:

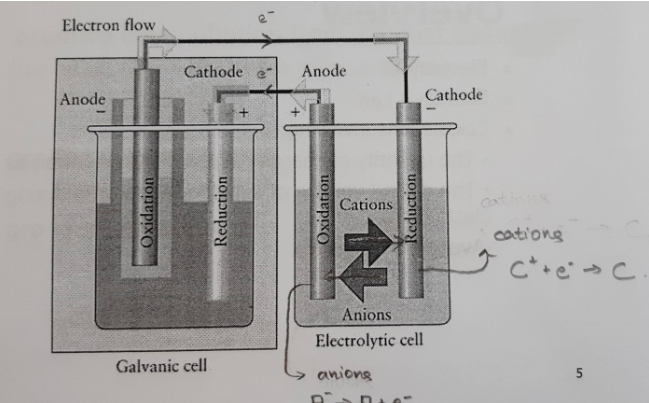
Jag fick just en insikt, tror jag. Vi får se om det stämmer.

En av sakerna jag inte kunde begripa var följande: när vi sluter kretsen fullständigt och elektrolyscellens anod sitter ihop med batteriets katod, så borde det ju ALLTID bildas en laddningsgradient mellan elektrolyscellens anod och batteriets katod. Så varför händer inget?

Kan det vara så att om den positiva ytladdnignen på katoden inte blir tillräckligt stor, så blir E-fältet inte tillräckligt starkt för att rycka bort elektroner från speciet vi vill oxidera? Så om vi vill oxidera t.ex. vatten och låt säga att batteriet är en Daniellcell, och ”spänningen inte är tillräckligt hög”, så innebär det att ytladdningen på kopparen ger upphov till ett E-fält som är för svagt, vilket gör att vi inte kan rycka bort elektroner ur vattenmolekylernas E-fält?

Och är det då kanske en liknande mekanism som förhindrar reduktion av rosten om spänningen är för låg; E-fältet som skapas mellan zinkanoden och rostkatoden, och fortplantar sig genom ledaren, blir inte tillräckligt starkt för att "tvinga" elektroner förbi de repellerande interaktionerna som elektronerna i rosten ger upphov till?

Om detta är fallet, då har jag ytterligare en fråga: varför behöver vi ens ett fullständigt batteri för att reducera rosten? Hade det i princip inte räckt med ett redoxpar (A/A²⁺) som har en hög oxidationspotential (låt säga t.ex. 10 V) och att rosten har en reduktionspotential vars absolutbelopp inte överstiger 10 V?

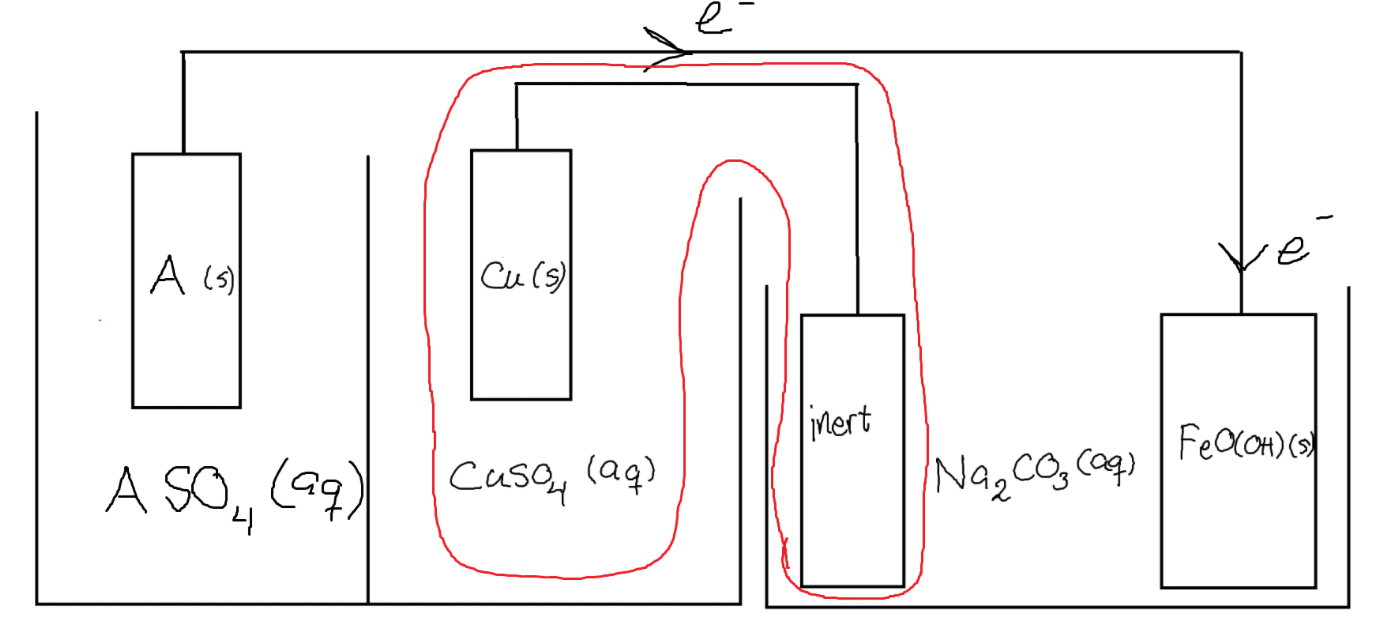
Här borde väl rosten reduceras oberoende av vad som händer mellan elektrolyscellens anod och batteriets katod. Så varför spelar det ens någon roll vad hela batteriet har för spänning? Vad spelar den inringade delen ens för roll? Det som är viktigt är väl de interelektrodiska spänningarna?

Du får ingen sluten krets utan det inringade området, det bildas ett överskott av positiv laddning längst till vänster i form av A2+(aq), dessa hindrar fler elektroner från att vandra och reducera FeOOH. T.ex. skulle sulfatjoner från CuSO4(aq) kunna vandra åt vänster för att motverka detta, men då har du ett överskott av positiv laddning vid kopparelektroden istället. Detta motverkas genom en reduktion där Cu2+(aq) tar upp elektroner som avges av den "inerta" elektroden. 

Men tänk om man sätter dit en saltbrygga då med nya joner (som jag antar att alla batterier har)?

Sätter du dit en saltbrygga får du ju en elektrolyscell och en galvanisk cell där den förstnämnda driver den sistnämnda?

Jag kanske missförstår vad du menar, men jag menade att man har en saltbrygga med något salt (typ kaliumnitrat kanske) i batteriet, för att utjämna laddningar:

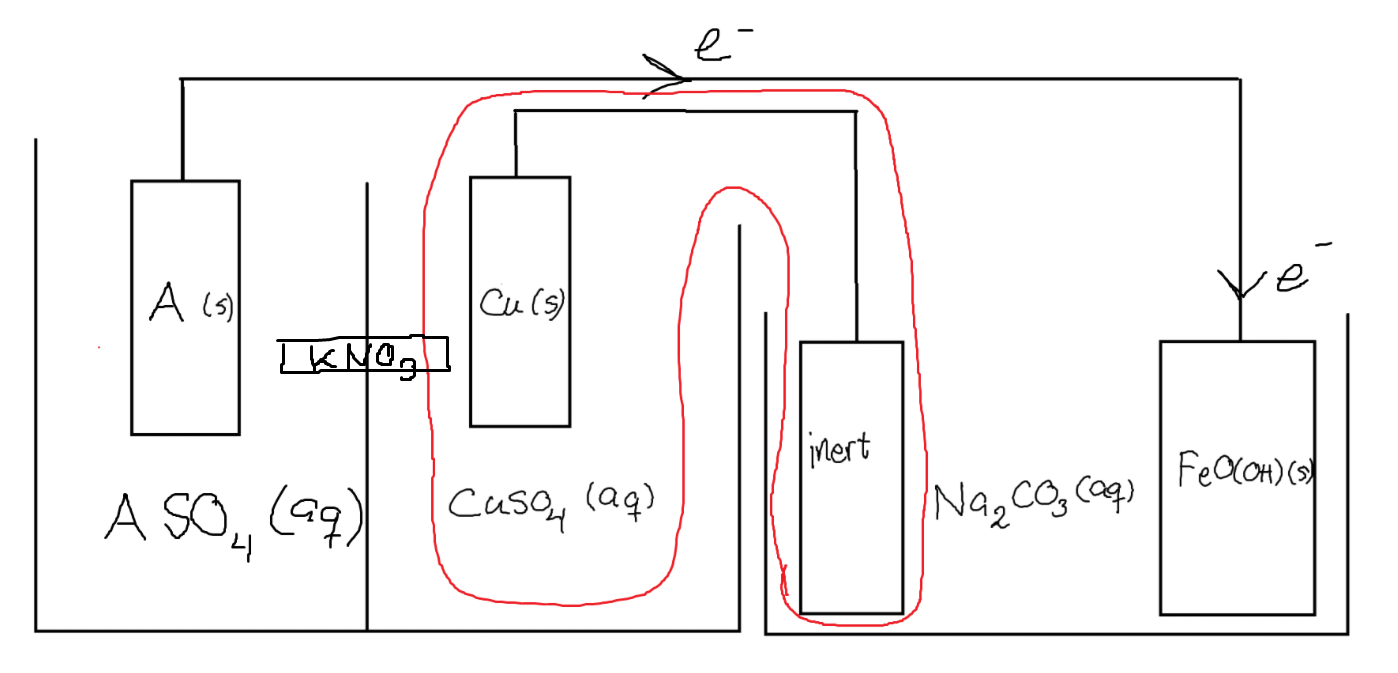
I det här fallet spelar det väl ingen roll vad som händer mellan kopparkatoden och den inerta anoden? Eller får man ändå samma problem som du belyste i #17? Det jag inte riktigt begriper är varför vi behöver ett helt batteri (en hel galvanisk cell), för det verkar ju som att en halv räcker med ett tillräckligt starkt reducerande redoxaktivt species.

Du får obalans i laddningarna även då, det finns inget sätt för sulfatjoner att färdas till halvcellen längst till vänster. I så fall blir kopparjonerna kvar och du ackumulerar positiv laddning vilket förhindrar flödet av sulfatjoner. Det behöver ske en reaktion vid elektroden du kallar "inert" som kan skapa ett flöde av elektroner till kopparelektroden så att kopparjoner kan reduceras och försvinna från lösningen.

Men behöver det verkligen vara sulfatjoner som färdas till vänster halvcell? Skulle det inte lika gärna kunna vara nitratjoner ur saltbryggan? 

Jo men då behöver sulfatjonerna transporteras till saltbryggan för att ta nitratjonernas plats,

Okej, det är väldigt rimligt.

Men rent principiellt hade man väl inte behövt driva reduktionen genom elektrolys; hade man inte istället kunnat låta rostbiten vara katod i en vanlig galvanisk cell? Så länge vårt redoxpar A / A²⁺ har tillräckligt hög oxidationspotential borde vi väl få reduktion?

Om du placerar dem i en gemensam elektrolyt skulle det fungera. Sen behöver man inte driva en elektrolyscell med en galvanisk cell, du kan använda en annan kraftkälla (t.ex. ett kraftverk där det sker någon fysikalisk process).

Okej, så är anledningen till att man brukar göra det med elektrolys mer av en praktisk fråga? Liksom, vem råkar bara ha redoxpar med hög oxidationspotential liggandes hemma?

Brukar göra med en galvanisk cell menar du? Ja, gör man det hemma är det nog den vanligaste spänningskällan.

Ja precis, jag undrade varför man tenderar till att göra rostborttagning genom elektrolys där man driver en elektorlytisk cell med ett typ batteri (eller liknande), när det principiellt hade gått att göra utan. Men det kanske bara är en rent praktisk fråga? Det är ju vara ganska vanligt att man råkar ha ett bilbatteri hemma jämfört med att man råkar sitta på starka reduktionsmedel.

Ja precis. Saltsyra är också väldigt bra på att lösa rost men det brukar man inte ha hemma.

Okej, fint! Då har jag nog bara en fråga kvar som berör uppställningen i #17, fast med generella redoxaktiva species A och B i batteriet:

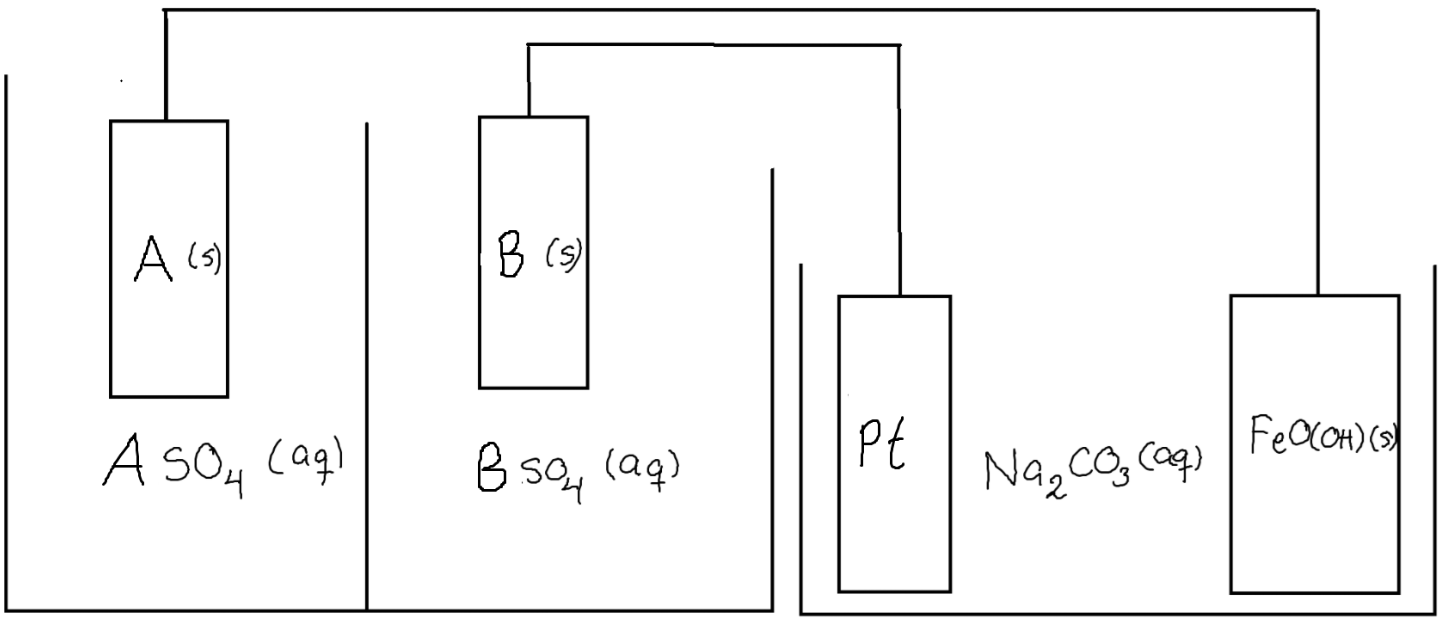
Och låt vidare reduktionen precis ske. I det här systemet kommer det ju finnas två spänningar, dels en spänning $\displaystyle \Delta V_1 = V_{\mathrm{FeO(OH)}}-V_{\mathrm{A}}$, och dels spänningen $\displaystyle \Delta V_2 = V_{\mathrm{B}}-V_{\mathrm{Pt }}$. 

Finns det något sätt att visa att dessa spänningar på något sätt är ekvivalenta med att titta på batteriets egna spänning, alltså visa att att betrakta dessa spänningar separat är detsamma som att säga "redoxreaktionen där rost reduceras har en spänning som exakt motsvarar batteriets spänning?". En bra början är väl att konstatera att $\Delta G \approx 0$ för hela systemet men längre än så kommer jag inte.

Spänningarna du beskriver finns inte, spänningen över dessa elektroder är 0V om man försummar resistansen i ledningarna. Däremot finns en spänning mellan A/B och Pt/FeOOH.

Okej, nu är jag väldigt förvirrad igen.

Är inte hela anledningen till att elektroner flödar från A till rosten att det skapas en negativ ytladdning på A jämfört med rosten => vi får en potentialskillnad => alltså en spänning som driver elektroner?

Och på motsvarande sätt från Pt till B?

I en öppen krets finns en sådan potentialskillnad, men så fort du sluter kretsen jämnas dessa laddningsskillnader ut och du får samma potential. Det kan man ganska snabbt inse om man helt enkelt tänker bort ledningen - i så fall befinner sig elektroderna i samma punkt och man kan bara ha en enda potential i en punkt. Det som driver systemet är egentligen potentialskillnaden mellan A och B, dvs A får en svagt negativ laddning till följd av reaktionen A(s) <--> A²⁺(aq) + 2e^- medan B får en svagt positiv laddning till följd av reaktionen B(s) <--> B²⁺(aq) + 2e^-. Att strömmen sedan kan färdas genom hela kretsen förutsätter att A är så pass oxiderande och FeOOH så pass reducerande att dessa kan utbyta elektroner. Likaså att reaktionen vid Pt kan utbyta elektroner med reaktionen vid B.

Jag hänger inte riktigt med. Om det endast finns en potentialskillnad mellan A/B och FeO(OH)/Pt, men ingen potentialskillnad mellan exempelvis Pt/B, vad är det som tvingar elektronerna att färdas från Pt till B? Om det inte finns något E-fält som kan tvångsoxidera vattnet färdas det väl inga elektroner?

Är inte hela grejen som gör att elektronerna flödar mellan t.ex. Pt och B just att det finns en potentialskillnad systemet försöker utjämna, dvs. B har en svagt positiv ytladdning jämfört med Pt?

Du kan se det som att det finns en infinitesimal potentialskillnad som gör att elektronerna kan röra sig genom kretsen, men skulle du mäta med en voltmeter över dessa elektroder (A/FeOOH eller B/Pt) skulle den visa 0 V.

Så det finns en potentialskillnad men den är så liten att den inte går att mäta?

Men om t.ex. spänningen mellan B/Pt är så liten, hur blir E-fältet så starkt att vatten oxideras?

Det är lättare att tänka att så fort det börjar skapas ett fält mellan A och FeOOH så nollställs det eftersom elektroner färdas över ledningen. Der blir en ”oändligt liten” potentialskillnad.

Det är fältet som skapas mellan A och B som löper genom hela kretsen och får bl.a. vatten att oxideras.

Men om fältet som skapas mellan A och B "fortplantar sig" genom hela systemet kan väl inte spänningen mellan B och Pt vara noll? Inom fältet måste det väl fortfarande finnas en potentialskillnad mellan punkten där Pt är och punkten där B är, annars hade väl inga elektroner flödat mellan dem?

Jag tror att ledningen förvirrar, så jag har ritat om din figur:

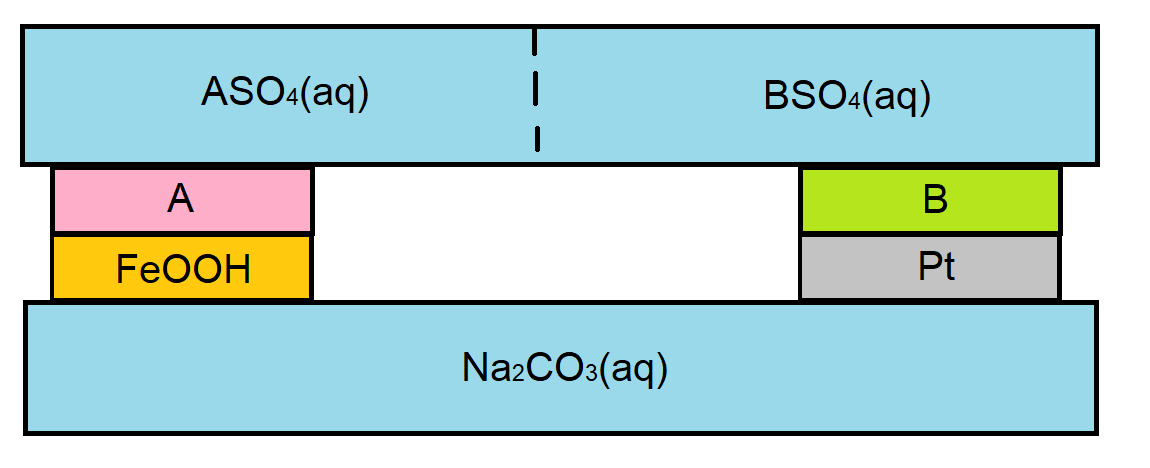
Så länge ledningen har försumbar resistans kan man rita figuren på detta sätt. Då kan man betrakta det som att A och FeOOH respektive B och Pt står i direkt kontakt med varandra. Om elektroner avges av A tas de omedelbart upp av FeOOH. Man kan också betrakta det som att det uppstår ett oändligt svagt fält mellan dessa, dvs så fort elektroner börjar frigöras vid A uppstår ett fält som omedelbart försvinner eftersom elektroner direkt tas upp av FeOOH. Motsvarande sker vid B och Pt.

Det som energimässigt driver processen är potentialskillnaden mellan A och B. A får en svagt negativ laddning pga jämvikten A(s) <--> A²⁺(aq) + 2e^- medan B får en svagt positiv laddning pga motsvarande jämvikt. Det uppstår då ett elektrisk fält mellan dessa elektroder, både genom elektrolyterna i den galvaniska cellen och genom hela elektrolyscellen. Överskottselektronerna vid A tas omedelbart upp av FeOOH, vilket får hydroxidjoner att gå ut i Na₂CO₃-elektrolyten, där de leder strömmen tillsammans med Na⁺-joner som leder strömmen i motsatt riktning. Vid Pt-elektroden sker oxidation av vatten vilket ger upphov till elektroner som omdelbart tas upp av B²⁺-jonerna. Då fås ett underskott av positiv laddning vid B vilket jämnas ut av motsvarande rörelse av joner genom elektrolyterna i elektrolyscellen.

Jag köper din omritning fullständigt och den är jag med på.

Det jag däremot inte begriper är hur fälten mellan A och FeO(OH) samt B och Pt kan vara "oändligt svaga". Jag tänker på följande vis:

Reaktionerna i jämvikten A (s) <--> A²⁺(aq) + 2e^- sker konstant. Så fort elektroner vandrar från A till FeO(OH) - tack vare potentialskillnaden som uppstår dessa emellan - så får vi ett underskott på elektroner i jämvikten och då löser det sig väl instantant ännu mer fast A för att återupprätta jämvikten, dvs. så fort elektroner vandrar iväg så bildas det direkt nya => fältet utjämnas aldrig och vi kan få ett kontinuerligt elektronflöde. 

Sedan tänker jag att samma sak sker vid Pt/B - jämvikten B (s) <--> B²⁺(aq) + 2e^- gör att det bildas ett överskott av positiv ytladdning på B. Systemet försöker utjämna detta genom att tvångsoxidera vatten vid platinaelektroden, men så fort elektroner tillkommer återupprättas jämvikten omedelbart genom att reducera mer B²⁺, så vi får aldrig någon nettoförändring i fältets storlek. Potentialskillnaden mellan ytan på B som är i kontakt med BSO₄ och platinaelektroden är ju tydligen stor nog för att oxidera vatten (som kräver spänning 1.23 V).

Jag tänkte vidare på detta i termer av Gibbs fria energi och det känns som om jag har kommit fram till något. Det kan hända att allt nedan är fel för att jag bygger resonemanget på felaktiga antaganden (t.ex. att spänningen mellan elektroderna inte är noll) men det känns suspekt rätt.

Om vi försöker tänka i termer av $\Delta V_1$ och $\Delta V_2$, (som kanske är försumbart små), så har vi följande:

För reaktionen som äger rum mellan A och FeO(OH) har vi:

$\Delta G_1 = -nF\Delta V_1$

och på motsvarande sätt har vi för reaktionen som äger rum mellan Pt och B:

$\Delta G_2 = -nF \Delta V_2$

Vi vet att om cellen precis drivs så har vi:

$\Delta G = \Delta G_1 + \Delta G_2 = 0$

Vilket innebär:

$\displaystyle nF\Delta V_1 + nF\Delta V_2 = 0 \iff \Delta V_1 + \Delta V_ 2 = 0$

Om vi skriver ut $\Delta V_1$ och $\Delta V_2$ explicit har vi:

$\displaystyle V_{\mathrm{FeO(OH)}}-V_{\mathrm{A}} + V_{\mathrm{B}}-V_{\mathrm{Pt}} = 0$

Omskrivning ger:

$\displaystyle V_{\mathrm{B}}-V_{\mathrm{A}} = V_{\mathrm{Pt}} -V_{\mathrm{FeO(OH)}} = -(V_{\mathrm{FeO(OH)}} - V_{\mathrm{Pt}})$

Så det visar sig alltså att spänningen i batteriet exakt måste motsvara spänningen mellan elektrolyscellens elektroder. Är inte det jag har visat här just att batteriets interna spänning exakt måste motsvara den sammansatta redoxreaktionens spänning?

Reaktionerna i jämvikten A (s) <--> A²⁺(aq) + 2e^- sker konstant. Så fort elektroner vandrar från A till FeO(OH) - tack vare potentialskillnaden som uppstår dessa emellan - så får vi ett underskott på elektroner i jämvikten och då löser det sig väl instantant ännu mer fast A för att återupprätta jämvikten, dvs. så fort elektroner vandrar iväg så bildas det direkt nya => fältet utjämnas aldrig och vi kan få ett kontinuerligt elektronflöde. 

I princip är detta rätt men eftersom elektroner färdas direkt fältet uppstår hinner det aldrig växa till, det var det jag menade med "infinitesimalt fält".

Så det visar sig alltså att spänningen i batteriet exakt måste motsvara spänningen mellan elektrolyscellens elektroder. Är inte det jag har visat här just att batteriets interna spänning exakt måste motsvara den sammansatta redoxreaktionens spänning?

Det du har visat är att spänningen den galvaniska cellen kan leverera minst måste motsvara spänningen som krävs för att driva elektrolyscellen, vilket är sant.

I princip är detta rätt men eftersom elektroner färdas direkt fältet uppstår hinner det aldrig växa till, det var det jag menade med "infinitesimalt fält".

Men om man inte sluter kretsen direkt så kommer väl potentialerna ha tid att byggas upp?

Det du har visat är att spänningen den galvaniska cellen kan leverera minst måste motsvara spänningen som krävs för att driva elektrolyscellen, vilket är sant.

Ja precis, men då utgick jag ju från att exempelvis $\Delta G_2$ är nollskild (eller?), och då kan väl inte $V_{\mathrm{B}} - V_{\mathrm{Pt}} \approx 0$? Är det inte till och med så att $V_{\mathrm{B}} - V_{\mathrm{Pt}} \ge 1.23\;\mathrm{V}$, eftersom potentialskillnaden mellan dessa punkter är tillräcklig för att oxidera vatten.

naytte skrev:

I princip är detta rätt men eftersom elektroner färdas direkt fältet uppstår hinner det aldrig växa till, det var det jag menade med "infinitesimalt fält".

Men om man inte sluter kretsen direkt så kommer väl potentialerna ha tid att byggas upp?

Ja

Det du har visat är att spänningen den galvaniska cellen kan leverera minst måste motsvara spänningen som krävs för att driva elektrolyscellen, vilket är sant.

Ja precis, men då utgick jag ju från att exempelvis $\Delta G_2$ är nollskild (eller?), och då kan väl inte $V_{\mathrm{B}} - V_{\mathrm{Pt}} \approx 0$? Är det inte till och med så att $V_{\mathrm{B}} - V_{\mathrm{Pt}} \ge 1.23\;\mathrm{V}$, eftersom potentialskillnaden mellan dessa punkter är tillräcklig för att oxidera vatten.

Nu när jag kollar ditt inlägg #41 igen ser jag nog att du har missförstått deltaG och deltaV, dessa bör beräknas i respektive cell, dvs mellan Pt/FeOOH respektive A/B. Slutekvationen blir densamma, därför missade jag det första gången jag läste vad du skrev. 

Jag tänkte mig snarare ett $\Delta G$ för nettoreaktionen som äger rum endast mellan t.ex. Pt och B:

$\displaystyle \mathrm{2B^{2+}+4e^- \longrightarrow 2B }$

$\displaystyle \mathrm{2H_2O \longrightarrow O_2+4H^+ +4e^-}$

Vilket ger:

$\displaystyle\mathrm{2B^{2+}+2H_2O \longrightarrow 2B+O_2+4H^+}$

Denna reaktion borde ju också ha ett $\Delta G$, och det var detta jag försökte ta fram ett uttryck för.

Det beskriver dock ingen nettoreaktion eftersom H+ och B2+ befinner sig i två olika elektrolyter som inte kan utbyta joner. Nettoreaktionerna sker mellan reaktionerna vid A/B respektive FeOOH/Pt. 

Kanske en väldigt elementär fråga, men varför måste jonerna befinna sig i elektrolyter som kan utbyta joner med varandra för att det ska kunna betraktas som en nettoreaktion? I de olika elektrolyterna finns det väl joner som kan balansera laddnigarna?

EDIT: eller jaha, om det blir för positivt i den ena t.ex. så kommer reaktionen upphöra.

Men varför ska man räkna på $\Delta G$ mellan A/B och FeO(OH)/Pt? Kanske är det så att det är mellan dessa reaktionerna sker "netto", men om man analyserar systemet så sker väl reaktionerna egentligen mellan A/FeO(OH) och B/Pt, alltså enligt hur de sitter ihop?

Reaktionerna sker på elektrodernas yta, dvs gränsskiktet elektrod/elektrolyt. Vad denna elektrod står i kontakt med via ledningen är egentligen ointressant ur kemisk synvinkel.

Men det är väl fortfarande så att elektronerna kommer från elektroden som den mottagande elektroden står i kontakt med via ledningen? För att elektroner ska flöda mellan dessa måste väl detta i sig vara termodynamiskt gynsammt, alltså borde man väl kunna räkna fram ett Delta G för bara den delen?

I princip inte, du kan tänka att hela galvaniska cellen är en "black box" där det inte spelar så stor roll vilken process (kemisk eller icke-kemisk) som sker så länge den levererar en spänning tillräckligt stor för att driva elektrolyscellen.

Det är just det här med att den galvaniska cellen "levererar en spänning" som jag inte kan förstå i det här fallet. I fallet med en galvanisk cell är det enkelt att förstå, där sitter elektroderna ihop direkt och man kan mäta en potentialskillnad direkt mellan dessa - inga problem. 

Men i det här fallet sitter ju elektroderna i den galvaniska cellen inte längre ihop, så det verkar väldigt märkligt att det är potentialskillnaden mellan dessa som skulle vara kritisk. Det kanske är så att det visar sig i slutändan att det räcker med att kolla på potentialskillnaden mellan dessa för att se om elektrolysen går att genomföra, men det känns mer som ett matematiskt resultat snarare än ett trivialt faktum man bara inser. Det måste väl gå att räkna fram att det är så? De sitter ju som sagt inte ihop så det hela verkar väldigt märkligt...

Tack för all hjälp och allt tålamod hittills, förresten.

Hej igen.

Jag diskuterade detta med en vän och han visade ett resonemang som är i linje med det jag har försökt göra här, och om det är rätt känns det som jag äntligen förstår detta. Vi får se:

Låt oss först analysera spänningen (hur liten den än må vara) mellan rostkatoden och anoden i den galvaniska cellen:

$\displaystyle \Delta V_1=V_{\mathrm{FeO(OH)}}-V_{\mathrm{A}}$

På samma sätt är spänningen mellan den galvaniska cellens katod och platinaanoden i elektrolyscellen:

$\displaystyle \Delta V_2=V_{\mathrm{Pt}}-V_{\mathrm{B}}$

Eftersom vi vill att rosten ska utgöra vår katod och att elektroner ska flöda bort från anoden kräver vi:

$\displaystyle \Delta V_1>\Delta V_2\iff V_{\mathrm{FeO(OH)}}-V_{\mathrm{A}}>V_{\mathrm{Pt}}-V_{\mathrm{B}}$

Om vi ordnar om termerna i olikheten kräver vi ekvivalent:

$\displaystyle V_{\mathrm{B}}-V_{\mathrm{A}}>V_{\mathrm{Pt}}-V_{\mathrm{FeO(OH)}}=-(V_{\mathrm{FeO(OH)}}-V_{\mathrm{Pt}})$

Eller med andra ord:

$\displaystyle \varepsilon_{\text{galvanisk cell}}> -\varepsilon_{\text{elektrolyscell}}$

Alltså det klassiska sambandet vi använder. Men kritiskt är att man tydligen kunde komma fram hit genom att gå "bakvägen" och kolla på spänningarna, hur små de nu än må vara, mellan elektroderna som sitter ihop istället för att kolla på den galvaniska cellens och elektrolyscellens interna spänningar.

Vad sägs om detta? Är det rimligt eller är det något som är fel i resonemanget?

Jag tycker det känns som ett knepigt sätt att angripa problemet, men jag kan inte med säkerhet säga att det är fel eftersom det kan vara jag som missar något i resonemanget. Jag tycker det är mer logiskt att börja angripa problemet med din näst sista ekvation, dvs konstatera att potentialskillnaden hos den galvaniska cellen måste vara större än dito hos elektrolyscellen för att man ska få en spontan process.

Men med tanke på att all algebraisk manipulation kan göras åt andra hållet måste det väl vara ett korrekt resonemang? Det vill säga, man kan utgå ifrån att $\varepsilon_{\text{galvanisk cell}} > \varepsilon_{\text{elektrolytisk cell}}$ (hur man nu kommer fram till detta?!), och ta sig till $\Delta V_1>\Delta V_2\iff V_{\mathrm{FeO(OH)}}-V_{\mathrm{A}}>V_{\mathrm{Pt}}-V_{\mathrm{B}}$.

Det är intressant det här, haha. Jag begriper inte hur man inser att utgångspunkten ska vara $\varepsilon_{\text{galvanisk cell}} > \varepsilon_{\text{elektrolytisk cell}}$, och du finner utgångspunkten jag föreslår här suspekt, även om de förefaller vara ekvivalenta (man kan gå från den ena till den andra).