Vad är en elektromagnetisk våg till skillnad från ett elektromagnetiskt fält?

Först kanske det skulle vara bra att definiera elektromagnetiskt fält. Kan man tänka att ett elektromagnetiskt fält är ett par av ett elektriskt och ett magnetiskt fält (B(r,t),E(r,t)) som kanske eller kanske inte satisfierar Maxwells ekvationer? 

Varför öppnar du för möjligheten att Maxwells samband inte skulle gälla vid något tillfälle?

Kan man vidare tänka att en elektromagnetisk våg är ett elektromagnetiskt fält som satisfierar Maxwells ekvationer i avsaknad av laddningar och strömmar?

Jag skulle säga att en elektromagnetisk våg består av oscillerande elektriska och magnetiska fält i avsaknad av elektrisk laddning. Laddningar och förskjutningar av laddningar behövs för att starta den elektromagnetiska vågen i till exempel en radiosändarantenn. När väl den elektromagnetiska vågen har släppt från antennen så "matar" vågen sig själv genom växelverkan mellan elektriska och magnetiska fältet enligt maxwells ekvationer.  

Varför öppnar du för möjligheten att Maxwells samband inte skulle gälla vid något tillfälle?

Jag hade ingen särskild anledning förutom att man rent matematiskt väl kan tänka sig att man bildar en tupel av ett elektriskt och ett magnetiskt fält som inte uppfyller Maxwells ekvationer? Jag försöker bara få rätt på definitionerna så jag kanske föreslår saker som är helt ofysikaliska.

Vad gäller vågdelen: så om vi har ett elektromagnetiskt fält, alltså ett par av ett magnetiskt- och elektriskt fält, $\mathbf{B}$, $\mathbf{E}$, och de alltså uppfyller vågekvationen,

$\displaystyle \frac{\partial ^2\mathbf{B}}{\partial t^2}=c^2\nabla^2 \mathbf{B}$

$\displaystyle \frac{\partial ^2\mathbf{E}}{\partial t^2}=c^2\nabla^2 \mathbf{E}$

Säger man att det elektromagnetiska fältet är en våg då?

Jag hade ingen särskild anledning förutom att man rent matematiskt väl kan tänka sig att man bildar en tupel av ett elektriskt och ett magnetiskt fält som inte uppfyller Maxwells ekvationer?

Jag _tror_ att man kan jämföra ungefär med newtons lagars överensstämmelse med verklighetens mekanik, dvs det kan säkert finnas avvikelser när kvantmekaniska eller relativistiska effekter börjar ta vid. I "vanliga fall" tycks det fungera precis som Maxwells ekvationer förutspår.

Vad gäller vågdelen: så om vi har ett elektromagnetiskt fält, alltså ett par av ett magnetiskt- och elektriskt fält, B, E, och de alltså uppfyller vågekvationen,

∂2B∂t2=c2∇2B

∂2E∂t2=c2∇2E

Säger man att det elektromagnetiska fältet är en våg då?

Jag vet inte om det finns någon strikt matematisk definition, men jag tänker mig att en företeelse som följer vågekvationen måste få betraktas som en våg iallafall.

Jag vet inte om det finns någon strikt matematisk definition, men jag tänker mig att en företeelse som följer vågekvationen måste få betraktas som en våg iallafall.

Men är det konventionellt att säga att fältet i sig är en våg då, eller hur skulle man uttrycka det?

Jag _tror_ att man kan jämföra ungefär med newtons lagars överensstämmelse med verklighetens mekanik, dvs det kan säkert finnas avvikelser när kvantmekaniska eller relativistiska effekter börjar ta vid. I "vanliga fall" tycks det fungera precis som Maxwells ekvationer förutspår.

Jag tror vi talar förbi varandra här. Strikt matematiskt kan man ju sätta ihop vilka magnetfält och elektriska fält som helst till en tupel, även om de absolut inte uppfyller Maxwells ekvationer (det vill säga, de kommer inte "av varandra").

Däremot är det säkert så att om man har ett fysikaliskt möjligt par av ett elektriskt- och ett magnetiskt fält, då måste de uppfylla Maxwells, som då kanske har samma axiomstatus som Newtons lagar i mekaniken?

Däremot är det säkert så att om man har ett fysikaliskt möjligt par av ett elektriskt- och ett magnetiskt fält, då måste de uppfylla Maxwells, som då kanske har samma axiomstatus som Newtons lagar i mekaniken?

Ja det är så jag menar. Vad menar du med tupel?

Jag kan som verklighetsnära exempel nämna att jag har en kollega som inte gör annat om dagarna än att bygga och köra komplicerade 3D-simuleringar av strömmar, spänningar, elektriska- och magnetiska fält. Det enda simuleringsverktyget gör är att lösa maxwells ekvationer, och de enda gångerna simulerat resultat inte stämmer med verkligheten är när man inte lyckas med indata, tex modellen eller randvillkor.

Många gånger är det ju dessutom jättesvårt att mäta hur verkligheten ser ut, utan man kanske bara kan observera följdfenomen av fälten.

Men är det konventionellt att säga att fältet i sig är en våg då, eller hur skulle man uttrycka det?

Ja, det är konventionellt.

Men är det konventionellt att säga att fältet i sig är en våg då, eller hur skulle man uttrycka det?

Ja, det är konventionellt.

Nä, nu pratar jag i nattmössan känner jag, jag läste din fråga fel. Det normala är nog att prata om fält och fältstyrkor och frekvenser när man mäter elektriska och magnetiska fält i luften (man ställer ju in frekvenser på radion tex). Ordet våg använder man nog mest ifall man vill beskriva något som kräver vågegenskaper för att kunna förklara, tex resonansfenomen. Tex i samband med den fysiska längden hos antenner eller andra ledande strukturer.

Högst applikationsberoende alltså.   

Det elektromagnetiska fältet är definierat i varje punkt i rumtiden och är den grundläggande byggstenen. Det existerar oberoende av om något rör sig eller inte.

En elektromagnetisk våg är en lösning till fältets ekvationer. I kvantfältteori kan man lite löst säga att en elektromagnetisk våg motsvarar ett koherent tillstånd av många excitationer (fotoner) som propagerar. Det är alltså tillståndet som propagerar.

Det jag själv minns tyckte var förvirrande då jag läste elmaggen var vad det egentligen fanns för samband mellan alla dessa spatiella fördelningar av elektriska och magnetiska fält ifrån källor av olika geometrier av laddning- och strömfördelningar som man räknade på (som såklart också uppfyllde vågekvationen), och den applikation som vi alla i vardagligt tal kallar för "kommunikation med hjälp av elektromagnetiska vågor". Jag minns att jag inte alls tyckte att det var självklart (och kanske är det egentligen det du frågar om?).

Jag tycker att grundkurselmag-litteratur är dålig på att förklara sådant. Förståeligt kanske då det inte ryms i bokens scope, men samtidigt är det ju en av de viktigaste elektromagnetism-applikationen av dem alla och borde iallafall finnas med som orientering, eftersom det ju är en viktig del av förståelsen (använder ni kanske Cheng i eran kurs?). Det beskrivs istället kanske i någon fortsättningskurs som kanske handlar om antennteori eller nåt.

Nedan klippte jag in en bild som visar en dipolantenn med elektrisktfält-fördelning, och hur fältlinjerna sluts när vågorna "släpper" ifrån antennen, för att sedan fortsätta att färdas i fria rymden utan att längre "matas" från källan av laddningar.

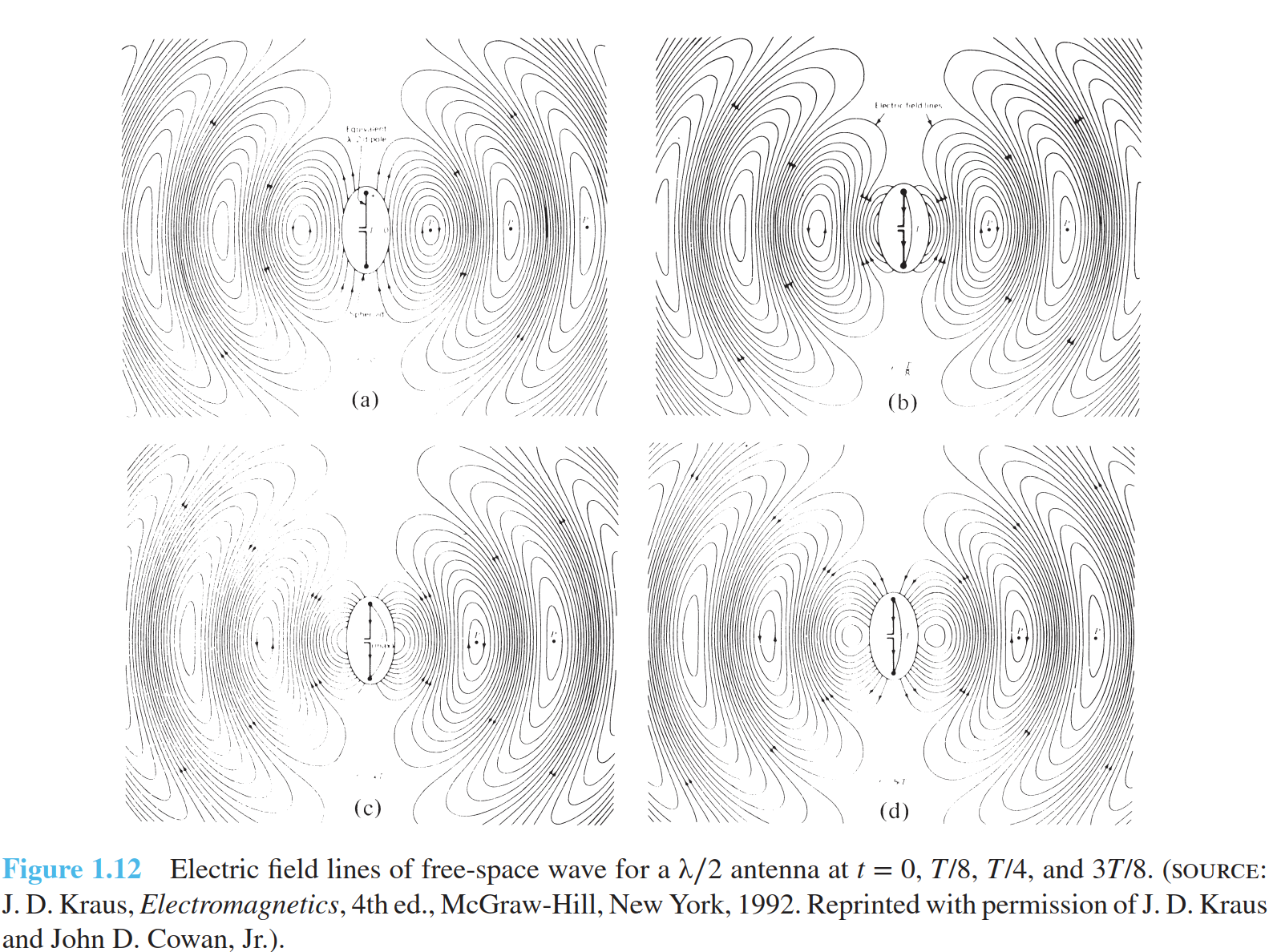
Hej, jag är tillbaka här igen och jag är fortfarande lite lost kring vad en elektromagnetisk våg är till skillnad från det elektromagnetiska fältet.

Om jag har förstått det rätt i resten av vågfysiken är en våg helt enkelt något som satisifierar vågekvationen. Är det inte det elektromagnetiska fältet i sig som uppfyller vågekvationen?

Är det mitt svar i #7 som gör att du tvekar om att  ett em-fältet inte kan vara en våg (med definitionen att em-fältet uppfyller vågekvationen)?

Det jag menade var bara att vilken _terminologi_ man använder beror på vad som är viktigt i sammanhanget. Pratar man om till exempel hälsorisker, eller ur störningssynpunkt, så använder man termer som beskriver fältstyrkor, tex amplituder  och frekvenser. Då är man ju intresserad av fältets egenskaper i en viss punkt i rummet.

Men pratar man om en radarfunktion så är ju fältets vågegenskaper nödvändiga för att kunna förstå utbredningshastighet, time-of-flight, reflektion etc.

Eller är det jag som inte riktigt förstår vad du frågar efter?

Du kan kanske få någon slags intuitiv känsla för detta genom att jämföra med vattenvågor. Vattenvågor är ju per definition "vågor" som man kan visa uppfyller en vågekvation, och visuellt kan observeras hur de breder ut sig i rummet över en vattenyta. Men om du står i en position i vattenbassängen och betraktar vattenytan i just din position så ser det ju bara ut som att vattennivån höjs och sänks med någon slags periodicitet och amplitud. Du kan i din position mäta vågornas "styrka" med till exempel en mätsticka.

Ungefär samma sak med em-vågor som du kan mäta elektrisk eller magnetiskt fältstyrka i en specifik position genom att placera ut någon form av antenn i positionen, och mäta inducerad ström/spänning i antennen. Samtidigt som de också breder ut sig i rummet ungefär som vattenvågor i bassängen.

Om det som förvirrar dig är hur två olika saker $B$ och $E$ kan sättas ihop till ett fält så går det till så att man utgår från en sorts tupel som du är inne på i inlägg #1. Man definierar potentialen $A_\mu = (\mathbf{A}, -\Phi)$ och strömvektorn $J^{\mu}=(\mathbf{J}, \rho)$, där vi använt konventionen $(+,+,+,-)$ med indexordning 1,2,3,0 $(x,y,z,t)$. I litteraturen används flera olika teckenkonventioner och det påverkar såväl strömvektor som hur vi ställer upp potentialen.

Sedan är det elektromagnetiska fältet $\mathbf{F}$ definierat som den antisymmetriska tensorn $F_{\alpha \beta}=\partial_\alpha A_\beta-\partial_\beta A_\alpha$ som uppfyller två fältekvationer (med dualbeteckningen $\bar{F}^{\alpha \beta}=\frac{1}{2}\varepsilon^{\alpha \beta\mu\nu}F_{\mu\nu}$):

$\partial_\alpha F^{\alpha \beta}=-J^{\beta}$ (Från Euler-Lagrange, ger Maxwell I och II)

$\partial_{\alpha}\bar{F}^{\alpha \beta}=0$ (Från Bianchi eller antisymmetrisk differentialform, ger Maxwell III och IV)

I grundkurser brukar man dock inte arbeta med det elektromagnetiska fältet som ett enda "fält", utan som en sorts växelverkan mellan $E$-fältet och $B$-fältet. Hur de växelverkar regleras genom Maxwells ekvationer. På samma sätt som Newtons ekvationer är en sorts approximation gäller Maxwells ekvationer under vissa begränsningar.

Det är viktigt att förstå att fältekvationerna är uppfyllda och att fältet existerar även för statiska elektriska och magnetiska "fält". Vidare "finns" det elektromagnetiskta fältet även i vakuum, utan att någon våg propagerar.