Hur går vi från vår formella definition av koordinater till "koordinatsystem"?

För att veta att man kan åskådliggöra koordinaterna på detta vis kanske man måste ha ett begrepp om vad "vinkel" betyder först. Det är ett tal men mer än så vet jag inte.

Precis! Genom att införa en skalärprodukt kan vi definiera ett längdbegrepp och ett vinkelbegrepp. Vi definierar längden av ett element (x,y) som roten ur skalärprodukten (x,y)*(x,y).

Sedan kan vi definiera vinkeln genom att säga att skalärprodukten mellan två element av längd 1 är cosinus av vinkeln mellan dem.

Okej, det är ett rimligt sätt att definiera vinkelbegreppet på (vi får givetvis normera våra vektorer innan vi tar fram vinkeln). Men hur vet vi att talet vi får ut motsvarar två vinkelräta vektorer i den geometriska tolkningen?

Jag hoppas jag förstår din fråga rätt.

Om vi definierar skalärprodukten geometriskt som

$v\cdot w := \|v\|\|w\|\cos\theta$,

och låter $e_1,\dots e_n$ vara en ortonormal bas, så gäller att

$v\cdot e_i = a_i$, där 

$v = \sum a_i e_i$.

Vi kan se detta genom att rita en bild. När vi tar skalärprodukten med en basvektor så projicerar vi på den basvektorn, och det vi får ut är exakt koefficienten framför den i:te termen i $v$.

Om

$w=\sum b_ie_i$, så är nu

$v\cdot w = v\cdot \left(\sum b_ie_i\right)  = \sum b_i(v\cdot e_i) = \sum b_ia_i,$

där vi känner igen den algebraiska definitionen av skalärprodukt i sista likheten (om vi skriver om det till $a_ib_i$).

Tillägg: 29 aug 2025 20:59

Jag utnyttjar här att $v\cdot aw = a(v\cdot w)$, där $v,w\in\mathbb{R}^n$ och $a\in\mathbb{R}$.

Jag har svårt att förklara vad jag menar och alla formuleringar jag kommer på låter bara dumma, så jag testar att bara ställa en fråga istället så får vi se vart det leder. Finns det något, rent principiellt, som hindrar oss från att rita vårt koordinatsystem så här, då vi jobbar i $\mathbb{R}^2$ med standardbasen:

Jag har väldigt svårt att förstå hur vi kan gå från våra abstrakta vektorbegrepp till en konkret geometrisk tolkning där vi kan uttrycka punkter i en bild. 

Jag vet inte om detta hjälper att besvara din fråga, men:

Det rent matematiska (ett vektorrum utrustat med en skalärprodukt) är bara en modell för verkligheten. Det är så att säga motiverat av verkligheten, men i sig självt är det ett abstrakt objekt som inte har någon visuell innebörd. Det är en mental konstruktion. Anledningen till att vi med fördel kan representera dessa abstrakta vektorer geometriskt (som verkliga objekt) är just eftersom den matematiska modellen (ett vektorrum med skalärprodukt) på ett tillfredsställande sätt beskriver en den verkliga, geometriska situationen.

Som vi kan se i mitt förra inlägg så stämmer den geometriska, "verkliga" versionen (där vi tänker oss att vi har pilar vars längder och vinklar vi kan mäta) överrens med den matematiska modellen. När vi sedan arbetar abstrakt med den matematiska modellen kan vi istället representera den med hjälp av geometriska figurer. Det är inget som är nödvändigt, men så klart väldigt användbart. Ju närmare vår matematiska modell beskriver något motsvarande verkligt fenomen, desto mer användbart blir det.

Det som inte skulle stämma överrens längre om vi ritade vårt koordinatsystem som på din bild är att vektorer som ritas vinkelräta inte längre skulle ha skalärprodukt lika med noll i vår matematiska modell. Omvänt så skulle vi kunna mäta upp en vinkel på mindre än 90 grader mellan två vektorer (säg, (1,0) och (0,1)) i bilden, men vars skalärprodukt är noll.

Man kan dock tänka sig en linjär transformation som förvränger talplanet till det du har ritat (som att vi tittar på talplanet från en vinkel istället för rakt ovanifrån). Det skulle motsvara ett basbyte. Så faktum är att din bild fortfarande fungerar hyfsat som hjälpmedel, men korrelationen till den matematiska modellen är nu försvagad.

Det hjälper definitivt!

En vidare fråga jag har är hur man definierar vinkelbegreppet. Om vi börjar med en skalärprodukt och definierar vinkeln $\theta$ mellan två normerade vektorer $\mathbf{x}_1,\mathbf{x}_2\in\mathbb{R}^2$ genom:

$\displaystyle \mathbf{x}_1\cdot \mathbf{x}_2 = \cos\theta$

så har vi inget sätt att veta hur denna vinkel ser ut i verkligheten, för då är det endast ett tal.

Om vi istället antar att vi kan mäta vinkeln, då måste vi alltså redan från början ha en geometrisk tolkning ($(1,0)$ pekar rakt åt höger, t.ex.). Men hur kan vi ha en geometrisk tolkning av vektorerna utan att redan veta vad en vinkel är? 

så har vi väl inget sätt att veta hur denna vinkel ser ut i verkligheten, för nu är det endast ett tal.

Precis, det är ett abstrakt begrepp som så att säga är inspirerat av verkligheten.

Men hur kan vi ha en geometrisk tolkning av vektorerna utan att redan veta vad en vinkel är?

Innan vi gör något formellt i matematiken, så vet vi vad vinklar och längder är, och vi kan definiera skalärprodukten som $\|a\|\|b\|\cos\theta$. Vi kan t.ex. mäta saker med gradskivor och måttband.

Separat kan vi nu definiera vektorrum och en särskild funktion som vi väljer att kalla skalärprodukt. I den här världen är "vinkel" bara ett namn på ett visst tal vi får ut av en viss funktion. Men begreppet vinkel betyder något även utanför matematiken. Vi använder alltså begreppet på två olika sätt här: det ena som ett resultat av en viss matematisk process, och det andra som det mer vardagliga, geometriska begreppet.

Det visar sig att på grund av hur vi valt att skapa denna matematiska modell, så stämmer den väl överrens med om vi ritar upp ett talplan med koordinater och börjar rita pilar i det och mäta saker med linjal och gradskiva.

Därför kan vi med fördel använda uppritade talplan med koordinater för att beskriva fenomen och processer i vår matematiska tankevärld.

Jag tror att det är $\cos$ (tillsammans med projektion) som kan ses som länken mellan det abstrakta och det geometriska här. Funktionen $\cos x$ är väldefinierad matematiskt, tror jag att vi tycker. Men den har samtidigt en enkel geometrisk tolkning - en roterande enhetslängd. Tänk enhetscirkel. Om vi tycker att den geometriska tolkningen är OK, så får vi samtidigt en geometrisk tolkning av begreppet projektion och då blir bilden av ortonormerade baser rätvinkliga (eftersom projektionen av dem på varandra blir 0).

Innan vi gör något formellt i matematiken, så vet vi vad vinklar och längder är, och vi kan definiera skalärprodukten som $∥a∥∥b∥\cos\theta$. Vi kan t.ex. mäta saker med gradskivor och måttband.

Men hur vet vi vad en vinkel är (mellan två "vektorer") innan vi ens har ett vektorbegrepp? Och hur kan vi veta vad en vinkel är innan vi gör något formellt?

Om vi börjar i den formella änden kan vi väl göra så här? Vi börjar med $\mathbb{R}^2$ utrustad alla trevliga operationer vi är vana vid. Vi kan även definiera vinkeln mellan vektorer genom skalärprodukten, men vi saknar då direkt geometrisk tolkning. När vi väl vill representera våra punkter hade vi väl lika gärna kunnat göra så här:

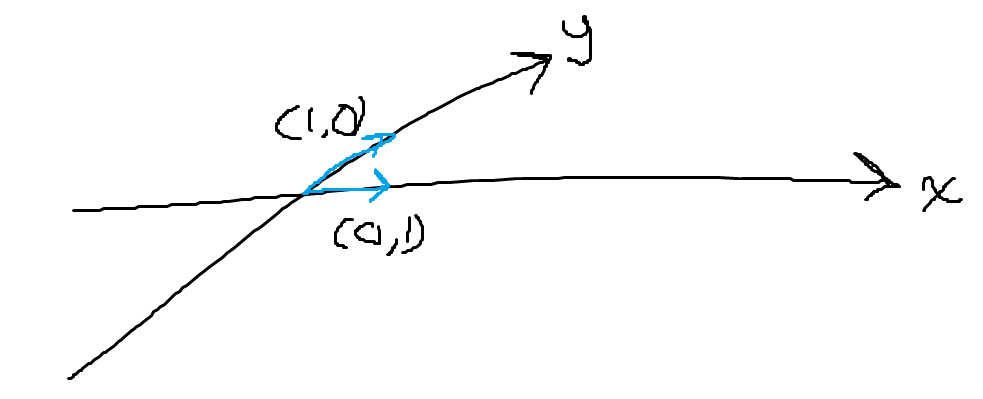
Rent principiellt kommer vi väl i detta koordinatsystemet kunna uttrycka exakt samma koordinater som i det vanliga koordinatsystemet, även om det kanske är mer otympligt. Vi behöver inte veta något om vinkelbegreppet. Kan vi alltså se det som att man har vinkelräta axlar av ren konvention (för att allting blir lättare), utan att ens behöva veta något om "vinklar"?

Vad gäller vinklar kanske man kan göra så här. Vi definierar enhetscirkeln som alla par av koordinater $(x,y)$ sådana att $x^2+y^2=1$. Kalla denna punktmängd $C$. Vi väljer sedan två normerade vektorer $\mathbf{x}_1,\mathbf{x}_2$. Dessa kommer sammanfalla med punktmängden $C$. Sedan kan vi definiera vinkeln $\theta$ som den minsta "båglängden" mellan dessa. Mer konkret kan vi (fungerar detta generellt?) beskriva $C$ med $\mathbf{r}(t)=(\cos t, \sin t)$. Antag att $\mathbf{x}_1$ har $x$-koordinat $a$ och $\mathbf{x}_2$ $x$-koordinat $b$. Då säger vi att vinkeln $\theta$ mellan $\mathbf{x}_1$ och $\mathbf{x}_2$ definieras som:

$\displaystyle \theta\left(\mathbf{x_1},\mathbf{x_2}\right):=\min\left\{ \int_{a}^{b}\left|\mathbf{r^\prime}\left(t\right)\right|dt,\int_{b}^{a}\left|\mathbf{r^\prime}\left(t\right)\right|dt \right\}$

Denna definition av vinkel blir väl oberoende av hur vi väljer att vinkla axlarna (vi får väl samma vinkel oavsett om axlarna är vinkelräta eller inte?). Skillnaden blir väl att vilken vinkel som "anses" vara t.ex. 90 grader ser olika ut i olika koordinatsystem. Så i ett koordinatsystem med en "vinklad" $y$-axel med basvektorerna skulle vi ha:

Vinkeln är oberoende av hur vi väljer att representera vårt koordinatsystem men hur vinkeln i sin tur ser ut beror på hur vi representerar koordinataxlarna.

Men hur vet vi vad en vinkel är (mellan två "vektorer") innan vi ens har ett vektorbegrepp? Och hur kan vi veta vad en vinkel är innan vi gör något formellt?

 Jag vet inte om jag förstår ditt rätt här, men:

Det finns väl rätt många sätt att tänka kring vinklar. Och vi har väl ett vektorbegrepp i geometrisk mening, dvs. som riktade pilar i rummet. Vi kan tänka på dem som riktade linjesegment till exempel. En vinkel är öppningen mellan två linjer som möts vid någon punkt. 

Den mesta matematiken har inte börjat i den formella ändan, utan tvärtom. Vi har sysslat med analys i årtusenden och det var väl inte förrän runt mitten av 1800-talet som de reella talen, vars existens man bara hade förutsatt, formellt konstruerades.

Man använde ju också fortfarande en slags naiv mängdlära som inte formellt axiomatiserats.

Rent principiellt kommer vi väl i detta koordinatsystemet kunna uttrycka exakt samma koordinater som i det vanliga koordinatsystemet, även om det kanske är mer otympligt. Vi behöver inte veta något om vinkelbegreppet. Kan vi alltså se det som att man har vinkelräta axlar av ren konvention (för att allting blir lättare), utan att ens behöva veta något om "vinklar"?

Jag svarade ju ungefär på detta tidigare. Det går utmärkt, men den geometriska skalärprodukten (längden av x gånger längden av y gånger cosinus av vinkeln mellan dem) i den grafiska representationen, som existerar långt innan en abstrakt definition, inte längre kommer stämma överens med den abstrakta definitionen (vektorerna (1,0) och (0,1) har en spetsig vinkel mellan sig rent visuellt, men deras "abstrakta" skalärprodukt är noll). Det går emot den motivation vi hade när vi definierade den formella skalärprodukten (som ett mått på hur mycket två vektorer har "samma" riktning).

Denna definition av vinkel blir väl oberoende av hur vi väljer att vinkla axlarna (vi får väl samma vinkel oavsett om axlarna är vinkelräta eller inte?)

Det är den abstrakta definitionen också. Om vi definierar

$\theta := \arccos\left(\frac{v\cdot w}{\|v\|\|w\|}\right)$

så påverkas inte det talet av hur vi väljer att rita en bild.

Men i övrigt kan du absolut fortfarande använda en sådan grafisk representation med en "skev" y-axel. Du kan väl dock bara definiera måttet på vinkeln genom den abstrakta skalärprodukten på precis samma sätt (så vinkeln mellan (1,0) och (0,1) fortfarande är pi/2). Det kommer bara inte vara samma som på din gradskiva.

Tillägg: 30 aug 2025 11:25

Det kanske inte riktigt är korrekt att säga att den geometriska skalärprodukten funnits långt innan. Det jag menar är att vektorer historiskt börjat som geometriska objekt för att representera kvantiteter som har en storlek och en riktning (t.ex. en kraft eller hastighet inom mekanik). Matematiska vektorrum har uppstått som en abstraktion av hur dessa fysiska objekt beter sig. Likaså har konceptet om vinklar funnits länge och i många olika former, och att definiera det via skalärprodukten är en modern definition. 

Tillägg: 30 aug 2025 11:32

Jag tror också att Peter har en poäng. De trigonometriska funktionerna har varit använda i över tusen år om jag inte minns fel.

Om vi vill kan vi dock definiera cos helt utan att referera till någon geometri (som realdelen av exp(ix), där exp(x) = 1 + x + x^2/2! + ...).

Det är den abstrakta definitionen också. Om vi definierar

$\displaystyle θ:=\arccos(\frac{v\cdot w}{∥v∥∥w∥})$

så påverkas inte det talet av hur vi väljer att rita en bild.

Så är det givetvis, och detta håller jag med om fullständigt. Jag försöker komma från perspektivet att vi inte redan har en geometrisk intuition, utan att vi går från något fullständigt abstrakt till något konkret, geometriskt. 

Det jag menade var att om vi vill ge vinkeln en mening utöver att det bara är ett tal och vi inte i förväg vet att den till synes godtyckliga definitionen $θ:=\arccos(\frac{v\cdot w}{∥v∥∥w∥})$ faktiskt råkar ge "vinkeln mellan vektorerna" (hur vi än väljer att rita axlarna finns det inget som säger att detta tal ligger "mellan" vektorerna, t.ex.), kanske vi måste definiera vinkelbegreppet på något annat sätt.

Men i övrigt kan du absolut fortfarande använda en sådan grafisk representation med en "skev" y-axel. Du kan väl dock bara definiera måttet på vinkeln genom den abstrakta skalärprodukten på precis samma sätt (så vinkeln mellan (1,0) och (0,1) fortfarande är pi/2). Det kommer bara inte vara samma som på din gradskiva.

Så för att vara tydlig: det är helt legitimt att rita axlarna hur man vill, och då kommer de vinklar som abstrakt är entydiga få nya grafiska representationer som inte nödvändigtvis stämmer överens med vår geometriska intuition ur vardagen?

naytte skrev:

Jag har svårt att förklara vad jag menar och alla formuleringar jag kommer på låter bara dumma, så jag testar att bara ställa en fråga istället så får vi se vart det leder. Finns det något, rent principiellt, som hindrar oss från att rita vårt koordinatsystem så här, då vi jobbar i $\mathbb{R}^2$ med standardbasen:

Jag har väldigt svårt att förstå hur vi kan gå från våra abstrakta vektorbegrepp till en konkret geometrisk tolkning där vi kan uttrycka punkter i en bild. 

Det kan man göra om man vill eller behöver ha ett sådant koordinatsystem. Det enda kravet är att basvektorerna är linjärt oberoende. Tänker man på polära, cylindriska och sfäriska koordinatsystem så behöver man inte ha räta linjer heller.

Det jag menade var att om vi vill ge vinkeln en mening utöver att det bara är ett tal

Hmm. Jag är inte säker på att jag förstår. Vad tänker du är något geometriskt? Om vi tänker oss något slags axiomatiskt system a la Euklides (syntetisk geometri), så räcker det väl att vi inför ett koordinatsystem och visar att den abstrakta strukturen vi definierat stämmer överens med den geometriska. Talet som vi kallar för vinkel verkar förändras på precis samma sätt som den geometriska vinkel som befinner sig där två vektorer möts, när vi flyttar runt vektorerna, antecknar deras koordinater och beräknar deras skalärprodukt och så vidare. Men i grunden är det ju bara ett tal. Det är som skillnaden mellan talet 0,5 och mitt halva äpple. Jag kan tillskriva talet till att representera äppelhalvor.

Kanske går det även att tänka lite mer intuitivt som Peter var inte på att när vi projicerar en vektor $v$ på någon vektor $w$ så får vi en vektor i riktningen $w$ men med längden skalad med $\cos\theta$?

Så för att vara tydlig: det är helt legitimt att rita axlarna hur man vill, och då kommer de vinklar som abstrakt är entydiga få nya grafiska representationer som inte nödvändigtvis stämmer överens med vår geometriska intuition ur vardagen?

Ja, alltså givet ditt vektorrum med skalärprodukt, som är ett abstrakt matematiskt objekt i grunden (men ofta avsett att modellera ett talplan med vektorer, avstånd och vinklar), så kan du ju rita vad som helst för att representera det. Du kan rita ett äpple om du vill. Det är bara att din representation inte är en så bra tolkning av det matematiska objektet (eller så är den så bra att den överskrider mitt förstånd). Som MaKe och jag nämner kan det ibland vara vettigt att använda skeva koordinataxlar (t.ex. om du vill illustrera effekten av en transformation).

Sidenote: Faktum är att transformationen från ett vanligt, kartesiskt koordinatplan med rätvinkliga axlar till ditt något skeva plan kan beskrivas med en linjär transformation. Abstrakt betyder det att transformationen bevarar addition och skalärmultiplikation av vektorer. Linjära funktioner är precis de funktioner som bevarar strukturer i vektorrum. Det betyder att vi t.ex. får samma resultat om vi först adderar två vektorer och transformerar deras resultat som om vi transformerar vektorerna separat och adderar deras resultat i det nya vektorrummet.

Geometriskt betyder linearitet av en funktion att origo lämnas oförändrad och att linjerna i rutnätet efter transformationen fortfarande är parallella och med jämnt avstånd mellan varandra.

Att transformationen är linjär betyder rent praktiskt att vi kan utföra vilka vektoroperationer vi vill i vilket av de två systemen som helst, och omvandla fritt mellan dem utan att förlora eller förvränga något (vi behöver så klart också att transformationen är bijektiv så att vi kan gå tillbaka).

Annan sidenote: En bra resurs som tangerar (i alldaglig bemärkelse) mycket av detta är Grant Sandersons material på linjär algebra (det är väldigt grundläggande, men ändå):

https://www.3blue1brown.com/lessons/vectors

https://www.3blue1brown.com/lessons/abstract-vector-spaces

EDIT: se #17 istället.

Hmm. Jag är inte säker på att jag förstår. Vad tänker du är något geometriskt?

Det jag menade var att om det enda vi har till en början är den formella definitionen av vektorrum så säger definitionen av "vinkel" ingenting om att det skulle vara någon typ av storhet "mellan vektorer", utan då är det endast ett tal. Man kanske vill ha en definition som bär med sig intuitionen om att det är något "mellan" två vektorer rent grafiskt. Helst ska denna definition också vara oberoende av hur vi väljer att representera koordinaterna. Problemet med enhetscirkeln som jag föreslog är väl att det blir beroende av val av koordinatsystem eftersom båglängden på cirkeln ändras i allmänhet då vi vrider koordinataxlarna runt origo.

Ja, alltså givet ditt vektorrum med skalärprodukt, som är ett abstrakt matematiskt objekt i grunden (men ofta avsett att modellera ett talplan med vektorer, avstånd och vinklar), så kan du ju rita vad som helst för att representera det. Du kan rita ett äpple om du vill. Det är bara att din representation inte är en så bra tolkning av det matematiska objektet (eller så är den så bra att den överskrider mitt förstånd)

Det är en mindre bra tolkning i bemärkelsen att den är jobbigare att jobba med, inte nödvändigtvis att den är mindre "rätt", eller hur? Det vill säga, sett ur perspektivet av ren matematik, har vi av "bekvämlighetsskäl" bestämt att vi ska rita axlarna vinkelräta mot varandra?

En sak jag däremot finner märklig är följande: låt säga att vi jobbar med mängden av alla koordinatpar (punkter) $(x,y)$ sådana att $x^2+y^2=1$. Vanligtvis skulle vi tolka denna punktmängd som en cirkel av radie 1, men är detta en tolkning som är bunden till våra typiska, kartesiska koordinater med vinkelräta axlar?

naytte skrev:

Det är en mindre bra tolkning i bemärkelsen att den är jobbigare att jobba med, inte nödvändigtvis att den är mindre "rätt", eller hur? Det vill säga, sett ur perspektivet av ren matematik, har vi av "bekvämlighetsskäl" bestämt att vi ska rita axlarna vinkelräta mot varandra?

Precis så, tycker jag. I kristallografi arbetar man med sneda koordinatsystem just eftersom det är bekvämre.

Jag tror jag har ett bra sätt att formulera min ursprungliga och övergripande fråga i ett tankeexperiment.

Antag att vi möter en alien som kan förstå ren matematik (i vårt symbolspråk) men som saknar fysikalisk och geometrisk uppfattning om vad begrepp som "vinkelrät" och "ortogonal" innebär. Vi förklarar för henne vad ett vektorrum är, vad en inre produkt är, vad addition är och så vidare. Vi beskriver för henne också vektorrummet $\mathbb{R}^2$ med den typiska basen, additionen, skalärprodukten och metriken. 

Vi ger henne nu en uppgift. Hon ska på ett papper nu skapa en strukturbevarande, visuell representation av vårt vektorrum genom att skissera två tallinjer som korsar varandra i en punkt vi kallar för origo, sådana att $\displaystyle \left(a,b\right)\in\mathbb{R}^2$ hamnar på koordinaterna $a$ längs den ena axeln och $b$ längs den andra.

Kommer det koordinatsystem hon skisserar nödvändigtvis ha, uttryckt i mänskligt språk, vinkelräta axlar, eller skulle axlarna kunna korsa varandra på ett sätt som vi inte hade kallat vinkelrätt?

Jag funderade vidare lite i dessa termer och jag kom fram till något intressant som jag inte riktigt förstår hur man ska tolka. Vi kan rent mängdteoretiskt definiera en cirkel $C$ med centrum i $(a,b)$ och radie $r$ som mängden av alla punkter $(x,y)$ som har avstånd $r$ till $(a,b)$ med avseende på den euklidiska metriken. Med andra ord:

$\displaystyle C:=\{ \left(x,y\right)\in\mathbb{R}^2: \left(x-a\right)^2+\left(y-b\right)^2=r^2 \}$

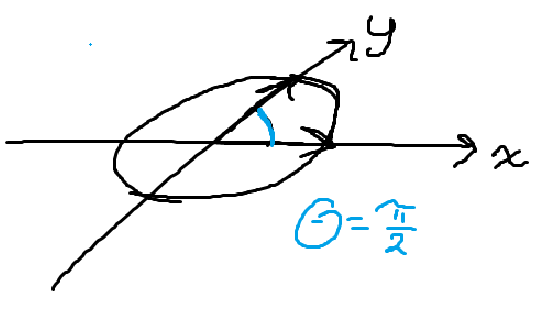
Denna definition är helt abstrakt och beror inte på någon visuell representation. Vi studerar nu två fall: i fall (a) ritar vi koordinatsystemet med axlar vi enligt intuition vet är ortogonala, och i fall (b) ritar vi koordinatsystemet med en liten lutning på $y$-axeln. Jag har framställt en grafik nedan:

Detta är samma punktmängd illustrerad i två olika val av koordinatsystem. Det finns ett enormt problem med (b): tydligen respekterar den framställningen inte den euklidiska metriken, för trots att mängden vi har avbildat är densamma så är avståndet inte $r$ mellan varje punkt på kurvan och $(a,b)$ i (b). Åtminstone är det så att pilarna mellan varje punkt i punktmängden och $(a,b)$ inte ser lika långa ut. Detta är en egenskap vi väldigt gärna vill ha, eftersom vi intuitivt tänker att två objekt som är lika långa också måste se lika långa ut. Så ett stort problem med att rita sneda axlar, och ett starkt argument för att axlarna ska vara ortogonala enligt vår vardagliga, geometriska intuition (vi vet intuitivt hur ortogonalitet ser ut), är att man med sneda axlar inte kan jämföra längder ordentligt; en vektor som ser längre ut än en annan kan egentligen vara kortare sett till vår metrik.

Vad tycker ni om detta? Är det rimligt? I så fall behöver man inte heller något begrepp om "vinkel" för att komma fram till att axlarna ska vara vad vi kallar vinkelräta. Allt vi behöver specificera är väl att längd i vektorrummet ska mappas "bijektivt" på längd på pappret?

Okej, här kommer ett till inlägg. Jag har tänkt vidare på detta och jag tror man kan tänka så här. Vi kan se den visuella framställningen som bilden av $\mathbb{R}^2$ under en funktion $F:\mathbb{R}^2\to \mathbb{R}^2_\text{papper}$. Vi:

(a) definierar "papprets metrik" $||u||_{\text{papper}}$ som mätetalet som erhålls vid mätning med linjal i en viss enhet

(b) definierar genom metriken en inre produkt på pappret, $\displaystyle\langle u,v \rangle_{\text{papper}}:=\frac{1}{2}\left(||u+v||_{\text{papper}}^2-||u||_{\text{papper}}^2-||v||_{\text{papper}}^2\right)$

Vidare kräver vi att $F$ ska vara sådan att:

$\exists c \in \mathbb{R}:\forall u \in \mathbb{R}^2: ||u||_{\mathbb{R}^2}=c||F(u)||_{\text{papper}}$

Det följer att:

$\displaystyle \forall u,v\in\mathbb{R}^2: u\cdot v = 0 \implies \langle u,v \rangle_{\text{papper}} = 0$

Med dessa två krav känns det som att det följer automatiskt att axlarna måste vara vinkelräta enligt vår vanliga, geometriska tolkning av "vinkelrät". Har inte tänkt vidare mycket mer än så här dock. Nu är det dags att slagga!

Ja, det ser bra ut. Ditt uttryck för papprets uppfattning om den euklidiska skalärprodukten (det linjära rummets inre produkt) kallas ibland polarisationsidentiteten.

Ditt krav "cirkeln får inte bli en ellips" motsvarar egentligen två krav. Dels isotropi (rotationsinvarians, det inte ska spela någon roll i vilken riktning vi mäter en längd), dels additivitet (summan (längden) av två "rätvinkliga" vektorer ska vara en rät linje enligt Pythagoras). Tillsammans med de vanliga reglerna för normen landar du i det euklidiska koordinatsystemet med vinkelräta basvektorer. Man kan också säga något viktigt om $g$ (kallas ibland Grammen eller M) och att vi inte behöver kräva ett ortogonalt system på papperssidan av $F$.

Alla inre produktrum $V$ av samma ändliga dimension $n$ med positivt definit inre produkt är isometriska. Upp till isometri finns det en unik bilinjär form $g: V\times V \to \mathbb{R} ,\, (u,v)\mapsto g(u,v)=\langle u,v\rangle$ som beskriver den inre produkten. I en bas $b_i$ ges matrisrepresentationen av $(g)_{ij}=\langle b_i, b_j \rangle$ och $g$ uppträder i sin absolut enklaste form ($\delta_{ij}$) precis då basen $b_i$ är ortonormal. Och det är just denna form som du visat är det vi människor föredrar för pappret.

Ditt uttryck för skalärprodukten kan också hjälpa oss konstruera perfekta cirklar, även med en skev bas / olika långa basvektorer som utgångspunkt. Den geometriska instruktionen "Skissa mängden av punkter $x$ som uppfyller $g(x,x)=1"$ ger alltid en perfekt cirkel med radie 1 och centrum i origo, oavsett basval. För att skissa cirkeln på ett platt papper i valfri bas behöver man bara kunna rita två linjärt oberoende basvektorer, mäta deras längder och använda matriselementen för $g$, dvs $\langle b_1,b_2\rangle$ som du visade för pappret ovan.

Detta löser väl för övrigt också problemet om vad "vinkel" betyder visuellt? Vi definierar vinkelbegreppet abstrakt genom skalärprodukten och sedan inser vi helt enkelt att vinkelfunktionen $\theta$ mellan $v$ och $u$ som definieras av:

$\displaystyle \theta \left(v,u\right):=\arccos\left(\frac{v\cdot u}{|v||u|}\right)$

hänger ihop med ett "unikt" utseende i vår visuella framställning. Vi behöver ingen "visuell variant" av vinkelbegreppet eftersom ett unikt vektorpar (1) ser ut på ett unikt sätt i framställningen samt (2) har en unik vinkel (upp till tecken på vektorerna).

Är det rimligt?

Ja, varje vektorpar definierar en bestämd vinkel $\theta$  (upp till valet av riktning på vektorerna). Sen får man komma ihåg att det finns andra vinkelbegrepp som du var inne på ovan, man kan till exempel se vinkeln som en koordinat. Då spelar det roll om vinkeln "växer" moturs eller medurs, alltså åt vilket håll vinkeln "som koordinat betraktat" växer eller minskar. Något sådant kan man inte få ut av just den här definitionen. 

För att bekanta sig lite med denna vinkeldefinition kan man ställa sig några frågor. Får $u,v$ vara noll? Vad är värdemängden för funktionen? Har vi något krav på definitionsmängden? Kan vi visa att kravet är uppfyllt?