Vad är skillnaden mellan nollmängder och udda/jämna funktioner?
Som fortsättning på den här tråden https://www.pluggakuten.se/trad/kvadrerbar-mangd/
så frågade jag vad de menar med : " 20200803204626-2.248.57.168.jpeg vad menas med den här satsen? Är det så att man kan "ta bort dom, de kan läggas till, eller ta bort utan att integrerandes värde påverkas" Sant? "
Som jag har fått förspörja så kan man tänka såhär med udda och jämna funktioner.
Förhåller de sig till varandra på något sätt?
Du frågar efter skillnaden, jag undrar lite försiktigt vad likheten är. Nollmängder är väl ett helt annat koncept än udda/jämna funktioner?
En jämn funktion är en funktion som är spegelsymmetrisk i y-axeln, så att y-värdet är oberoende av tecknet på x-värdet (). Ett par exempel är (både 3 och -3 ger y=9) eller . En udda funktion är "tvärtom" () så att x och -x ger samma y-värde fast med omvänt tecken. T.ex. (x=2 ger y=8, x=-2 ger y=-8), eller .
En nollmängd är väl en mängd med "oändligt liten" area (eller volym)?
"Förspörja" var f.ö. ett spännande ord. Inte hört förut!
Skaft skrev:Du frågar efter skillnaden, jag undrar lite försiktigt vad likheten är. Nollmängder är väl ett helt annat koncept än udda/jämna funktioner?
En jämn funktion är en funktion som är spegelsymmetrisk i y-axeln, så att y-värdet är oberoende av tecknet på x-värdet (). Ett par exempel är (både 3 och -3 ger y=9) eller . En udda funktion är "tvärtom" () så att x och -x ger samma y-värde fast med omvänt tecken. T.ex. (x=2 ger y=8, x=-2 ger y=-8), eller .
En nollmängd är väl en mängd med "oändligt liten" area (eller volym)?
"Förspörja" var f.ö. ett spännande ord. Inte hört förut!
Men tänkte, för i den url-länken jag skickade, så står det att om en rand är (säger man är, eller har?) en nollmängd, så kan man tänka att den inte ger något i integrationen, och det är därför jag fick en idé - om att de är lika man tänker med udda och jämna funktioner?
hehe förspörja, var med i något högskoleprov förut, kunde det inte, och har lagt det på minnet för livet nu ^^^
Nej, det är inte så det hänger ihop. I en udda funktion är funktionsvärdena för de positiva x-värdena samma som för de negativa x-värdena, men med ombytt tecken. Om man integrerar en udda funktion över ett intervall som är symmetriskt m a p y-axeln blir integralen 0, eftersom den "positiva ytan" på ena sidan om axeln är lika stor som den "negativa ytan" på den andra sidan. För en jämn funktion är funktionsvärdena för de positiva x-värdena samma som för de negativa x-värdena. Om man integrerar en jämn funktion över ett intervall som är symmetriskt m a p y-axeln blir integralen dubbelt så stor som integralen från 0 till ena sidan.
Om du integrerar något som är 0 blir integralen 0 för att den är 0 (något förenklat).
Däremot skulle man kunna säga att randen är så tunn att arean för området innanför blir lika stor oberoende av om man inkluderar själva randen eller inte.
Antar att du då tänker på när man integrerar en udda funktion och får noll? Det är av symmetriskäl. Se t.ex. sin(x) från x=-2 till x=2:
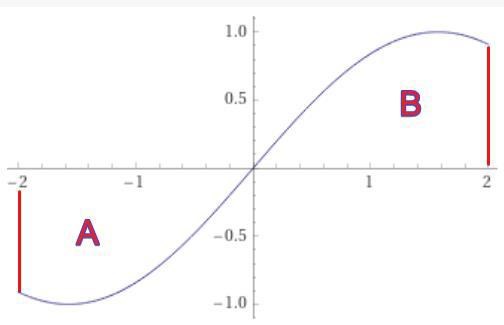
Område A ligger under x-axeln och kommer därför bidra negativt till integralens värde, medan område B ligger ovanför och bidrar positivt. Områdena är lika stora, så integralens värde blir 0. De tar helt enkelt ut varann.
Att randen inte bidrar till integralen innebär t.ex. att en integral blir samma oavsett om man tar med ändpunkterna eller inte, dvs. det spelar ingen roll för integralens värde om man betraktar definitionsmängden som eller .
Skaft skrev:Antar att du då tänker på när man integrerar en udda funktion och får noll? Det är av symmetriskäl. Se t.ex. sin(x) från x=-2 till x=2:
Område A ligger under x-axeln och kommer därför bidra negativt till integralens värde, medan område B ligger ovanför och bidrar positivt. Områdena är lika stora, så integralens värde blir 0. De tar helt enkelt ut varann.
Att randen inte bidrar till integralen innebär t.ex. att en integral blir samma oavsett om man tar med ändpunkterna eller inte, dvs. det spelar ingen roll för integralens värde om man betraktar definitionsmängden som eller .

Men så symmetrier.. då tar blir det 0.. och dessa då.. förstår inte vad som med att "lägga til och ta bort"
Varför tror du att den sidan du har lagt in skulle ha något med udda/jämna funktioner att göra?
Det felresonemanget jag vill diagnostisera sannakarlsson1337 med är helt enkelt att båda begreppen har vagt att göra med att något med integralens värde försvinner/är noll.
Det stämmer, men begreppen har inget med varandra att göra. Meningen med nollmängden är att övertyga dig om att integralens värde inte påverkas av "strimlan"/"skivan" (alltså randen), det spelar alltså ingen roll om du integrerar på en öpppen eller sluten mängd.
Om du symmetriskt integrerar en udda funktion får nu noll (gäller både i en och flera dimensioner (förutsatt att integrationsområdet också är symmetriskt)), men det är inte pga nån egenskap hos randen!
En bottenarea med area noll är en nollmängd.
Qetsiyah skrev:Det felresonemanget jag vill diagnostisera sannakarlsson1337 med är helt enkelt att båda begreppen har vagt att göra med att något med integralens värde försvinner/är noll.
Det stämmer, men begreppen har inget med varandra att göra. Meningen med nollmängden är att övertyga dig om att integralens värde inte påverkas av "strimlan"/"skivan" (alltså randen), det spelar alltså ingen roll om du integrerar på en öpppen eller sluten mängd.
Om du symmetriskt integrerar en udda funktion får nu noll (gäller både i en och flera dimensioner (förutsatt att integrationsområdet också är symmetriskt)), men det är inte pga nån egenskap hos randen!
Jahaaa.. nu tror jag att jag förstår!
Niiiiice, återkom med fler frågor!




