Vad är skillnaden på viskösa krafter och "shear stress" och hur propagerar hastighet i en fluid?
Hej!
Jag håller på att läsa i vår kursbok om transportfenomen och är i delen som behandlar fluiddynamik. Ett begrepp jag fortfarande inte riktigt greppar, även efter att ha läst samma passager i boken om och om igen, är vad "shear stress" är i en fluid, och vad skillnaden mellan "shear stress" och viskösa krafter är. Som exempel har jag målat en enkel figur som illustrerar en fluid mellan två parallella plattor med avstånd från varandra, där den undre plattan är orörlig och den övre plattan rör sig med en hastighet till följd av att den utsätts för en kraft i samma riktning som hastigheten:
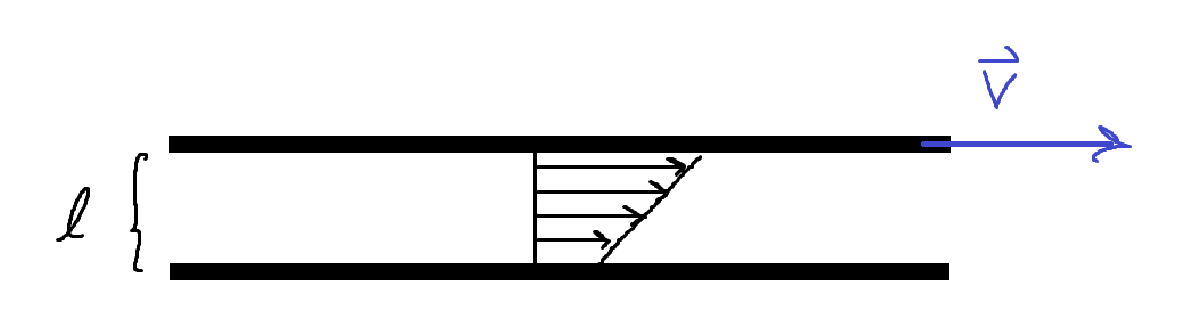
Så som jag förstår det kan man tänka ungefär så här. Det faktum att den övre plattan rör på sig gör att det lager närmst plattan kommer "dras med" tack vare intermolekylära interaktioner (t.ex. van der Vaals-växelverkan) mellan fluidens molekyler och plattan. Eftersom detta lager också växelverkar med lagret under sig kommer detta också dras med om än med något lägre hastighet, och så fortplantar sig rörelsen nedåt, lager för lager. Kan man formalisera denna heuristiska beskrivning med differentiela fluidelement eller något liknande?
Eftersom plattan dras med en kraft kommer den påverka det närmsta lagret med kraft enligt Newtons tredje lag, och då kommer det närmsta fluidlagret dra lika hårt i plattan åt andra med en kraft . Samma fenomen propagerar nedåt i fluiden eftersom alla lager växelverkar med varandra. Utgör detta fenomen det man kallar för viskösa krafter eller är det det man kallar för shear stress? Vad är skillnaden på de två?
När man googlar på viskösa krafter så verkar man mena krafter som motverkar rörelse i allmänhet, jmf friktion. Det inkluderar både "normalkrafter" (riktade längs normalen för någon yta, se bild nedan) och skjuvkrafter (riktade längs med någon yta).
Spänningar i normalriktning motsvaras av diagonalelementen i spänningstensorn (stresstensor). Skjuvspänningar (shearstress) motsvaras av de utomdiagonala elementen. Nu kan man så klart lägga sitt koordinatsystem som man vill och då byter normalkrafter och skjuvkrafter plats.
När jag bläddrar i min gamla bok så härleder man t.ex. navier-stokes genom att titta på infinitesimala volymselement. I nedanstående bild (från boken) har man ritat ut de 6 resulterande krafterna på varje sida av fluidrätblocket. Varje sådan kraft kan man dela upp I normalkraft och skjuvkraft (i förhållande till sin yta). Men som sagt, koordinatsystemet och rätblocket kan man orientera hur man vill. Ditt resonemang om den rörliga plattan tycker jag är bra. Med brasklappen att viskösa krafter är allt som motverkar en rörelse, inte bara skjuvkrafter. I ditt exempel finns bara skjuvkrafter.

Tack för svaret!
Så om jag har förstått det rätt är en skjuvkraft en kraft som ligger prallellt med ytan? Vad är då en skjuvspänning? Detta verkar vara någon slags "kraft över area" men vad är arean i det fallet? Skjuvkraften ligger ju längs ytan och angriper i en punkt så det är lite oklart vilken area man skulle använda då.
Spänning (skjuv- och normal-) är mycket riktigt kraft per area, precis som tryck (som ju är en tryckande normalspänning). Och skjuvkrafter är parallella med någon yta, verklig eller tänkt. Kraften som du behöver för att dra i din platta ovan för att bibehålla konstant hastighet motsvarar summan av alla skjuvkrafter från fluiden. Själva skjuvspänningen är då F/A, där A är plattans area. Egentligen inte konstigaste än att luften trycker med ca 100kN på varje kvadratmeter vid normalt lufttryck. Det "saknas" angreppspunkt där också.
I exemplet med ett infinitesimalt volymselement, dV, så kommer sig skjuvkrafterna av att övrig fluid påverkar dV, precis som i ditt resonemang om hur hastigheten "propagerar nedåt" i plattexemplet. Arean här är då en sida av dV, som i min bild ovan. Man kan så klart tänka sig en godtycklig form på dV.
Ett annat exempel (som nog inte tillför mer info än ditt plattexempel) skulle kunna vara ett pappersark, med arean A, i en vindtunnel orienterat så att vinden möter kanten av papperet. Då är normalspänningarna försumbara och man behöver bara motverka skjuvkrafterna för att hålla fast arket. Vi tänker oss för enkelhetens skull att flödet är laminärt. Skjuvspänningar finns på bägge sidor av arket och ytan är då 2A.
Okej, jag tror att jag är med. Jag tror att jag blev förvirrad av att min bok använde samma notation ( för både skjuvspänning och skjuvkraft i olika sammanhang.
Under vilka betingelser blir skjuvspänning, "definierad" som resultantkraften av alla skjuvkrafter över en yta genom dess area, ett användbart mått? Vad gör vi för antaganden om kraftfördelningar längs ytan et cetera? Har skjuvspänning kanske en mer allmän definition över infinitesimala areaelement, som man sedan kan integrera över en hel yta för att få ett punktvis beroende av skjuvspänningen längs ytan, som man kan med t.ex. tryck i rummet? Alltså så att man får en funktion som t.ex. .
Min bok är väldigt snål med detaljerna här eftersom det av någon anledning förutsätts att man redan ska kunna detta.
Intressanta frågor, även om jag kanske inte alltid förstår vad du menar.
Under vilka betingelser blir skjuvspänning, "definierad" som resultantkraften av alla skjuvkrafter över en yta genom dess area, ett användbart mått?
I min bild ovan använder man de resulterande krafterna (både normal och skjuv) för att härleda navier-stokes ekvationer genom att applicera newtons 2:a lag på dV. Det känns iaf användbart.
Vad gör vi för antaganden om kraftfördelningar längs ytan et cetera?
När det handlar om infinitecimala dV så är fördelningar inte så intressant, gissar jag. När det gäller din platta kan ju fördelningen ge mer eller mindre vridande moment på plattan kring "z-axeln".
Har skjuvspänning kanske en mer allmän definition över infinitesimala areaelement, som man sedan kan integrera över en hel yta för att få ett punktvis beroende av skjuvspänningen längs ytan, som man kan med t.ex. tryck i rummet? Alltså så att man får en funktion som t.ex. τ=τ(x,y,z,t)
Om vi fetstilar dina här så kommer vi ganska nära hur man modellerar detta. Jag menar att då är en tensor som alltså innehåller "all" spänningsinformation, både normal (på diagonalen) och skjuv (övriga element). Det innebär att vi har en tidsberoende spänningstensor i varje punkt i ett flöde. Ett tidsberoende tensorfält i helt enkelt.
Kanske kan det ge något att läsa under definition här?
Ekvationen för en isotrop, Newtonsk fluid som flödar laminärt verkar besvara en av frågorna jag hade,
där är hastighetsfältet (mer riktigt kanske "fartfältet i flödesriktningen"?) hos fluiden i vad jag antar är ett fullt utvecklat flöde (så att är invariant under translationer i flödesriktningen)?
Här har vi ju skjuvspänningen som en funktion av punkter i fluiden. Det var mest detta jag undrade; om skjuvspänning egentligen är något man tillskriver en punkt snarare än ett helt område av fluiden, vilket det verkar som om man implicit gör i t.ex. plattexemplet ovan där man tänker att skjuvspänningen ges av "skjuvkraftsresultanten längs ytan delat med dess area".
Nu när jag tittar i boken igen kan jag inte undvika att bli förvirrad igen. Man skriver exempelvis att betyder "skjuvspänningen som är normal mot planet i -riktningen". Mycket tal om riktning. Jag hade uppfattningen om att skjuvspänning är en skalär men tydligen verkar det vara någon slags vektorstorhet? Eller menar man att man ska använda storleken en skjuvkraft som är normal mot i -riktningen?
Hmm, ja, jag känner också av förvirringen. En kraft (vektor) delat med en skalär (area) blir ju en vektor. (Såvida man inte ser arean som en riktad area, vilken man gör ibland.) Då blir även spänningen en vektorstorhet.
Citatet
skjuvspänningen som är normal mot planet z=x i y-riktningen
Är väl goddag yxskaft? En normal till z=x har väl ingen y-komponent, om jag inte fintar bort mig själv nu?
Kanske hjälper denna. Den svenska versionen har spänningstensorn vid första bilden. De utomdiagonala elementen kan man kalla och indexsiffrorna kan du byta ut mot x, y och z. Dvs , kolla även den engelskspråkiga sidan. De brukar vara utförligare och mer korrekta.
Så här har man skrivit i boken:

Jag fattar ingenting här om jag ska vara ärlig. Skjuvspänning som jag hade tolkat det tidigare är en skalär, som i t.ex. sambandet i #7 där man får en punktvis definierad skalär i fluiden.
Tydligen är shear stress i sig en tensor (tydligen inte längre ett element ur spänningstensorn...?) och tydligen ska man också ha riktning...?! Men sedan i andra sammanhang så räknar man med skjuvspänningen som om det vore en skalär, t.ex. i exemplet på bara nästa sida

Jag fattar ingenting
Ajajaj, det låter ju inte alls bra! Jag tror att du är nära. Det är nog mest petitesser i kombination med kanske ett inte helt stringent, konsekvent språk i boken. När det gäller boken så ser jag inga direkta fel. Jag tycker att jag är med på noterna. Det gäller bara för mig att försöka förklara så att någonannan kan förstå 😀
Om vi börjar med #7 ovan. Det handlar om ett 1-dimensionellt flöde. Vi kan ha ditt plattexempel i tankarna här. Som den är skriven så är allt skalärer men det betyder inte att det saknas riktningar på storheterna. Tecknet på derivatan och tecknet på ger riktningen. Du kan se det som en vektorekvation med fetstilta och . Om plattan flyttas åt höger så byts tecknen jämfört med om den hade flyttats åt vänster. Du är nog med på att om u är en vektor så är du/dy också det.
Jag håller med om att boken inte är så noga med att tala om när det är en vektor eller inte. T.ex. är ekvation 7-2 enbart skalärer. Viskositet har ingen riktning. (Åtminstone inte i en sådan här kurs.) Det betyder att täljare och nämnare inte heller har riktning.
Tydligen är shear stress i sig en tensor
När det gäller spänningstensorn och dess komponenter så ser jag det så här: tensorn är en 3x3-matris med skalära element. Varje element är normen av en spänningsvektor utökat med minustecken ifall spänningen är motriktad koordinataxeln som den är riktad längs. Tensorn innehåller all spänningsinformation i en punkt (eller mer fysikaliskt, i ett litet volymselement).
Vi tar ett exempel. Vi väljer att titta på ytan längst till höger i bilden i #2. Det finns förmodligen en likande bild i din bok. Ytan påverkas av en resulterande kraft i arbiträr riktning. Det är den kraften som är utritad. Det är resultanten av alla "små kraftpilar" som finns utspritt över ytan. Antagandet här, gissar jag, är att dessa krafter är hyfsat homogent spridda eftersom det är en liten volym. Dela upp denna resultant i x1-, x2- och x3-komposanter. Då blir x1-komposanten en normalkraft mot ytan. Om du dividerar med ytans area, , så får du normalspänningen. De andra 2 komposanterna är skjuvkrafter (eller spänningar om du delar med arean) längs med ytan, riktade längs de andra koordinataxlarna. Med notationen i figuren i #2 kan man kalla dessa för resp. . Om t.ex. är motriktad x3-axeln så är den negativ. Gör sen likadant för de andra ytorna och summera (med tecken) spänningar som är riktade längs samma axel. Då kan man sammanfatta spänningssituationen för volymselementet i en 3x3-matris. Denna tensor representerar spänningstillståndet i en punkt (med volymselementet som omgivning). Till varje punkt i ett flöde kan man alltså ordna en (tidsberoende) spänningstensor. Med den och newtons andra lag modellerar man flödet och får ett gäng partiella diffar för hastigheten.
Tillägg: missade att påpeka att t.ex. , dvs med din boks notation, är då ett element i spänningstensorn, positivt eller negativt. Det representerar en skjuvspänning på ytan definierad av att z-axeln (första indexet på ) är normal till ytan och att skjuvspänningen är parallell med y-axeln (andra indexet på ).


