Vad betyder denna notation?
Halloj!
Jag håller på att göra gamla tentauppgifter och har stött på notation jag inte vet hur man ska tolka. Den ser ut så här:

Vad betyder notationen ?
Jag har inte sett den heller men jag gissar att det är någon sorts paremetriserad kurva? Alltså den första "inputten" i parentesen är x-värdet och den andra, y värdet. Men samtidigt verkar det då inte riktigt finnas någon poäng med att skriva den på det sättet. Blir bara en vanlig funktion..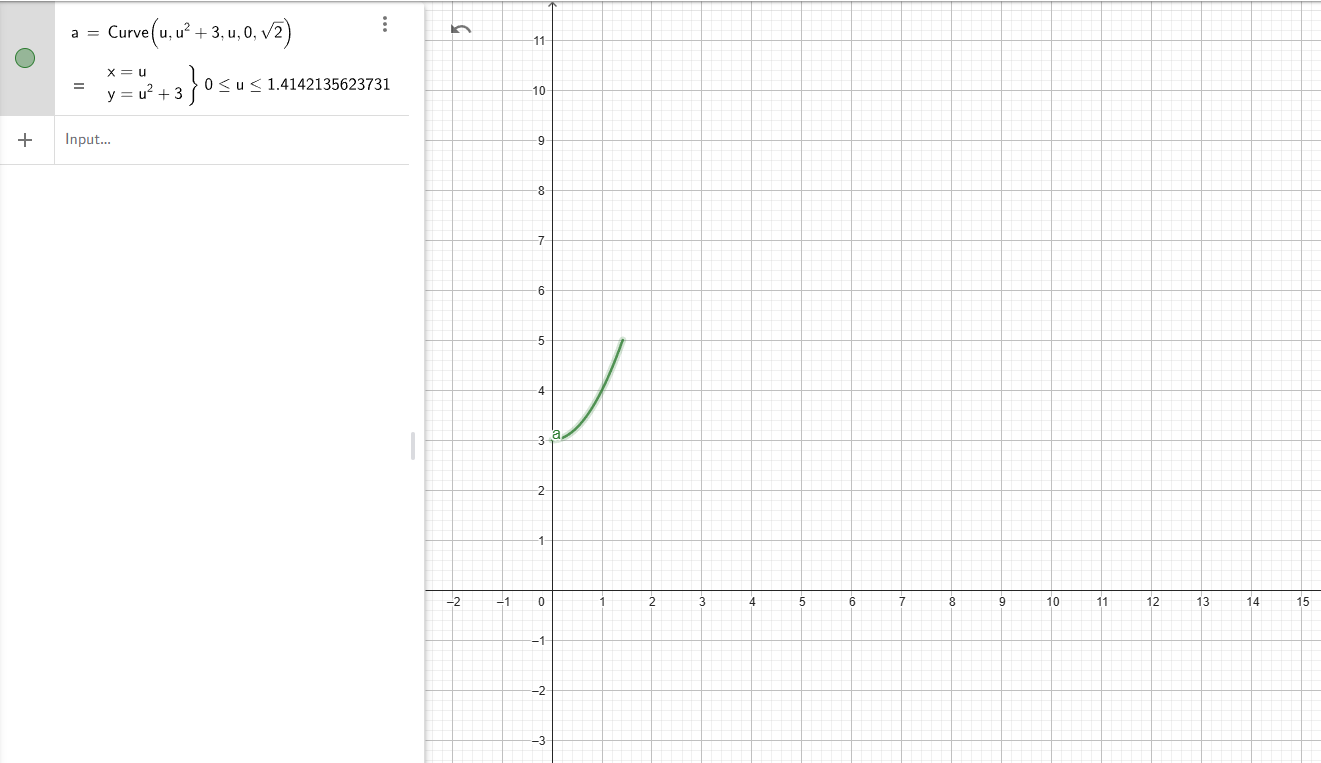
Ja, så kan det vara. Verkade bara konstigt med tanke på att det blir en helt vanlig funktion, som du säger 🤷
Det är helt enkelt en kurva i parameterform. "Generellt" kan det skrivas på intervallet . Detta kanske gör dig klokare.
Eller ja, ett sätt att skriva den på parameterform, vanligare är väl kanske
med .
Det ser ut som att författaren till frågan inte kunde bestämma sig för om den vill tänka på sin kurva som funktionen definierad av eller mängden (aka bilden av ), och därför hittade på en egen notation i ett försök att göra bådadera samtidigt!
Okej, så en funktion som spottar ut en vektor i då helt enkelt, det kan jag köpa. Men hur ska man tolka detta rent grafiskt? Är tolkningen helt enkelt en samling punkter som ligger i -planet? (alltså den helt vanliga grafen ).
Eller ska man bara tolka det som att den spottar ut en punkt i xy-planet? Eller spelar det ingen roll hur man väljer att se det?
Är det någon (praktisk) skillnad mellan en punkt (x,y) och (orts)vektorn r=(x,y) (i detta fall)? (Parenteserna är för att jag inte är säker på svaret själv, och la in några alternativ som kanske förändrar svaret…?)
Det finns en viss praktisk skillnad,
kallas en parameterframställning för kurvan . Definitionsområdet är det slutna begränsade intervallet i . Värdeförrådet blir, om är kontinuerlig, en sammanhängande begränsad punktmängd i
I allmänhet väljer man parameterframställningen så att den positiva genomloppsriktningen motsvarar växande värden på parametern. Kurvan är alltså orienterad.
Notera att i vänsterledet är ortsvektorn, men i högerledet står istället en funktion som är koordinatberoende. Ibland skriver man det som
En punktmängd i planet, liksom en i rummet orienterad kurva, är oberoende av i vilket koordinatsystem vi beskriver den. Funktionen ger däremot olika "värden" beroende på i vilket koordinatsystem vi uttryckt den. Det kan verka som lite hårklyveri, men brukar klarna när man arbetar med flera olika koordinatsystem.
Jag tror att jag förstår. Skulle detta kunna vara ett annat exempel på en orienterad kurva ?
Så om jag har förstått det rätt så genererar HL en koordinat i medan VL är ortsvektorn till den punkten. Om det här exemplet är OK så tror jag att jag förstår notationen i frågan också.
Japp, nu har du definierat en cirkel! Om vi följer växande värden på din parameter vandrar vi runt cirkelbågen moturs tills vi kommer tillbaka till startpunkten. Om ändpunkterna i intervallet sammanfaller på ett sådant sätt (dvs ) kallas kurvan sluten.
Om du deriverar din funktion med avseende på parametern, dvs får du en tangent till kurvan. Differentialen bildas genom
Differentialen kallas ibland kurvans linjeelement. Mycket användbar vid linjeintegraler!
På samma sätt kan du parametrisera ytor och volymer samt andra objekt i olika antal dimensioner. Parameterframställningar är viktiga i bland annat flervariabelanalys, vektoranalys och differentialgeometri.




