Vad blir utfallsrummet och händelserummet i detta fall?

Kanske räcker det med ett träd?

först tre grenar, en för varje maskin.  /med lika sannolikheter (1/3)/ FEL!
med sann. enl texten,  0,6 resp 0,3 resp 0,1 

sedan  två grenar från varje maskin (defekt, perfekt) med  de i texten angivna (betingade) sannoliheterna.

Räkna ihop utfallen i trädtopparna   etc

Yes, jag är med på själva beräkningen och att man kan göra ett träddiagram (personen i videon ritade snällt nog upp ett också!).

Jag undrar mer över hur man skulle kunna dränka detta i matematisk formalism (för det är mycket mer intressant än själva uppgiften).

Varför krångla till det mer än nödvändigt?
Trädet i sig är väl formellt nog.
Går att generalisera åt alla håll…

Här är diagrammet ur videon, där $D$ betecknar defekt och $\overline{D}$ betecknar motsatsen till defekt.

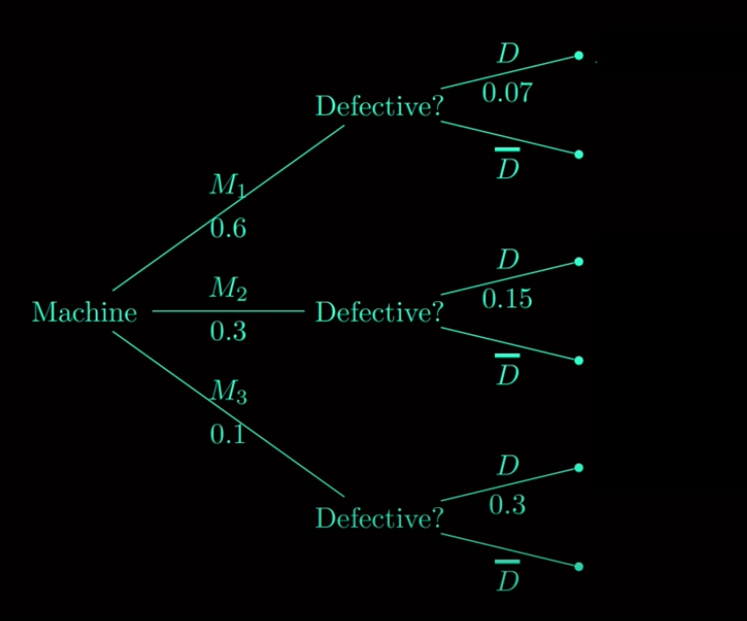
Senare i videon så skriver han t.ex. uttryck som $\displaystyle \mathbb{P}(M_1\cap D)=0.\!6\cdot0.\!07$. Det verkar då för mig som att $M_1$ och $D$ är händelser snarare än element i ett utfallsrum. Men är dessa då händelser ur samma händelserum eller kan det finnas flera olika händelserum samtidigt?

Det är detta jag inte riktigt får ihop. Att lösa uppgiften är inget konstigt utan det här är mer av en detaljfråga på petitessnivå. 

Tillägg: 15 maj 2025 12:05

Jag vet inte om händelserum är rätt begrepp på svenska men jag syftar på den svenska motsvarigheten till "event space", som är en delmängd av potensmängden av "sample space".

[Glömde sann. för maskinerna, har nu redigerat så det stämmer m ditt träd]

Utfallsrummet ser jag som punkterna i trädtopparna, var och en med sin sannolikhet. 
Trädet visar bara hur man kommer dit.

Händelserna är delmängder av utfallsrummet   (på vanligt sätt).

Skulle inte det räcka som formalisering?

Håller med om ovan: Sample space är trädtopparna med kardinalitet 6 och Event space är alla möjliga delmängder (måste nödvändigtvis inte vara alla delmängder, men överkurs...)

Kanske man istället kan se det som 2 stokastiska variabler (??), $X$  har sample space $\{M1,M2,M3\}$ och $Y$ med sample space $\{D,\bar D\}$. Totala sample space blir nu 2-dimensionell med kardinalitet 2*3=6 som innan.... Bara en fundering, vet inte om detta kan vara formellt korrekt.

Om det är någon sats du är ute efter för att göra detta ”formellt” så är det ju satsen om total sannolikhet som används. 

Om man vill ha med all information är det nog lättast att se ufallsrummet som produkten

$\Omega_1\times\Omega_2,$

precis som Calle och Arktos är inne på.

En händelse som exempelvis $\{(M_2,0),(M_2,1)\}$ utgör då händelsen att en del producerades av maskin 2.

(0: defekt, 1: felfri)

Det är kanske lite underligt att tänka på frågan på detta sätt. Jag skulle bara tänka som ni i tidigare inlägg att händelsen att en del är defekt är beroende av händelsen att delen var producerad av en viss maskin, och antingen göra ett träddiagram (egentligen onödigt) eller använda lagen om total sannolikhet (precis det du gör i din intuitiva beräkning). Formellt det är det dock ordnade par i utfallsrummet.

Tänk att du kastar ett mynt två gånger. Ufallsrummet för varje kast är $\Omega=\{\text{krona}, \text{klave} \}$, medan utfallsrummet för hela experimentet ges av alla möjliga ordnade par $(\omega_1,\omega_2) \in\Omega\times\Omega$.

Precis, det var precis detta jag var ute efter!

Ville bara säkerställa att det går att tänka på det som ett rum $\Omega_1 \times \Omega_2$. Vill inte ta för givet att saker bara ska gå, oavsett hur många smarta matematiker som har tänkt på det förr!

Tack för hjälpen allihopa!