Vad innebär påståendet?

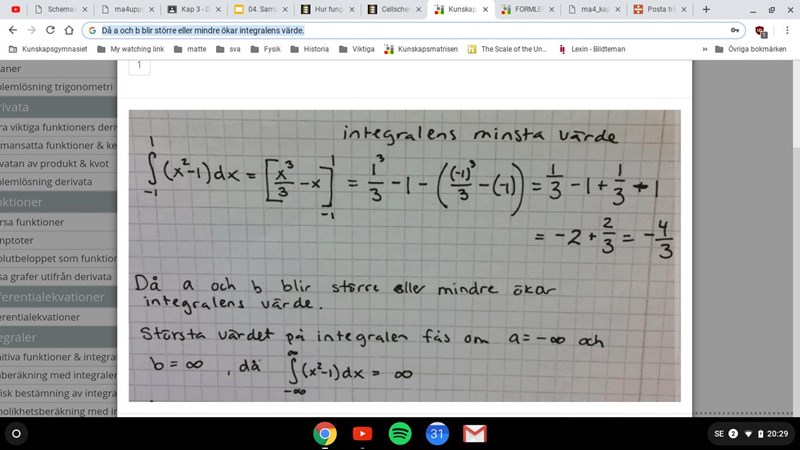
Mariam1999 skrev:

"Då a och b blir större eller mindre ökar integralens värde."

fattar inte vad de innebär, det står i facit såhär:

Hur lyder uppgiften?

(Om du skissar grafen till $x^2-1$ så ser du att minsta värdet fås vid angivna värden på a och b. Alla andra värden på a och/eller b ger ett större värde på integralen.)

Yngve skrev:

Mariam1999 skrev:

"Då a och b blir större eller mindre ökar integralens värde."

fattar inte vad de innebär, det står i facit såhär:

Hur lyder uppgiften?

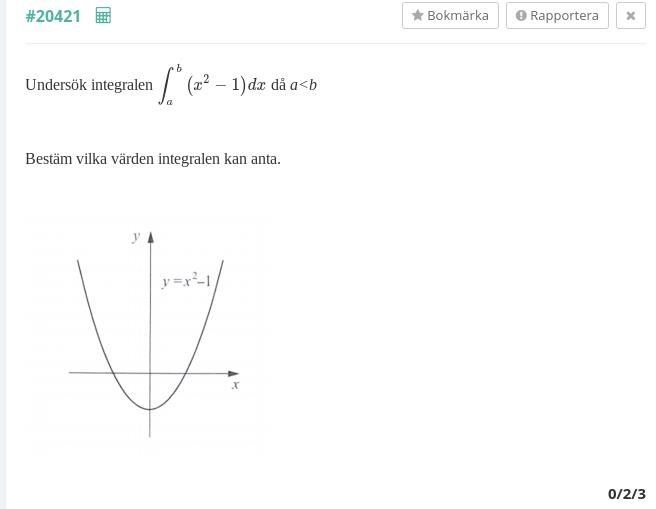
Det framgår inte vad a och b är för något, men det står att nån integral har sitt minsta värde, antagligen beroende av a och b. I så fall kan a och/eller b öka eller minska i värde (alltså, ändras) och då kommer integralens värde att öka.

Funktionen $x^2-1$är ständigt växande för större x-värden större än 1 och för x-värden mindre än 1.

Ex. $$\begin{gathered} x=1 -> f\left(x\right)=1^2-1=0 \\ x=2 -> f\left(x\right)=2^2-1=3 \\ x=10 -> f\left(x\right)={10}^2-1=99 \\ x=100 -> f\left(x\right)={100}^2-1=999 \end{gathered}$$

Eftersom integralen är arean under kurvan så kommer arean bli större och större desto längre vi väljer att integrera

${\int }_0^1{x}^2-1 dx <{\int }_0^4{x}^2-1 dx < {\int }_0^{10}{x}^2-1 dx <{\int }_0^{100}{x}^2-1 dx<{\int }_0^{1000}{x}^2-1 dx$

Funktionen växer dock också på andra sidan grafen om vi skulle välja mer och mer negativa y-värden

$$\begin{gathered} x=-1 ->f\left(x\right)=(-1{)}^2-1=0 \\ x=-2 -> f(x)= (-2{)}^2-1=3 \\ x=-10 -> f\left(x\right)= (-10{)}^2-1=99 \\ x=-100 -> f(x)= (-100{)}^2-1=999 \end{gathered}$$

Alltså desto längre vi integrerar åt vänster i negativ riktning, desto större blir arean under grafen och integralen alltså

${\int }_{-1}^0{x}^2-1 dx <{\int }_{-4}^0{x}^2-1 dx < {\int }_{-10}^0{x}^2-1 dx <{\int }_{-100}^0{x}^2-1 dx<{\int }_{-1000}^0{x}^2-1 dx$

Titta här gå grafen

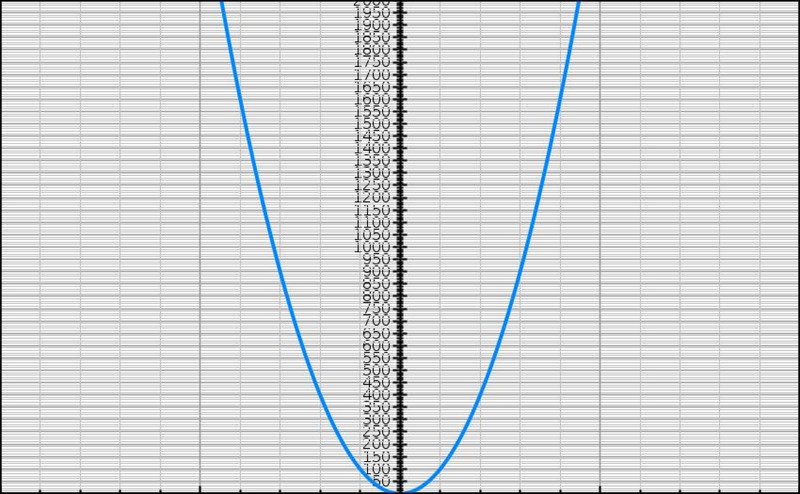
a och b är integrationsgränserna och både när vi integrerar längre och längre åt höger(låter ena gränsen bli större) och när vi integrerar längre och längre åt vänster(låter ena gränsen blir mindre och mindre/mer negativ) så ökar arean/integralen.

Låt oss säga att vi väljer att integrera både långt ut åt höger och långt ut åt vänster ex.

${\int }_{-1000}^{1000}{x}^2-1dx$ då får vi en väldigt stor integral/area eftersom vi täcker in stora delar av grafen ovan.

Den allra största arean får vi om vi går ända ut till oändligheten åt båda hållen eftersom vi då täcker in hela arean under grafen.

${\int }_{-\infty }^{\infty }{x}^2-1dx$ och arean blir då oändligt stor eftersom grafen bara fortsätter och fortsätter åt båda håll och inte har något slut, även om det kanske inte syns så bra på bilden

Jonto skrev:

Funktionen $x^2-1$är ständigt växande för större x-värden större än 1 och för x-värden mindre än 1.

Ex. $$\begin{gathered} x=1 -> f\left(x\right)=1^2-1=0 \\ x=2 -> f\left(x\right)=2^2-1=3 \\ x=10 -> f\left(x\right)={10}^2-1=99 \\ x=100 -> f\left(x\right)={100}^2-1=999 \end{gathered}$$

Eftersom integralen är arean under kurvan så kommer arean bli större och större desto längre vi väljer att integrera

${\int }_0^1{x}^2-1 dx <{\int }_0^4{x}^2-1 dx < {\int }_0^{10}{x}^2-1 dx <{\int }_0^{100}{x}^2-1 dx<{\int }_0^{1000}{x}^2-1 dx$

Funktionen växer dock också på andra sidan grafen om vi skulle välja mer och mer negativa y-värden

$$\begin{gathered} x=-1 ->f\left(x\right)=(-1{)}^2-1=0 \\ x=-2 -> f(x)= (-2{)}^2-1=3 \\ x=-10 -> f\left(x\right)= (-10{)}^2-1=99 \\ x=-100 -> f(x)= (-100{)}^2-1=999 \end{gathered}$$

Alltså desto längre vi integrerar åt vänster i negativ riktning, desto större blir arean under grafen och integralen alltså

${\int }_{-1}^0{x}^2-1 dx <{\int }_{-4}^0{x}^2-1 dx < {\int }_{-10}^0{x}^2-1 dx <{\int }_{-100}^0{x}^2-1 dx<{\int }_{-1000}^0{x}^2-1 dx$

Titta här gå grafen

a och b är integrationsgränserna och både när vi integrerar längre och längre åt höger(låter ena gränsen bli större) och när vi integrerar längre och längre åt vänster(låter ena gränsen blir mindre och mindre/mer negativ) så ökar arean/integralen.

Låt oss säga att vi väljer att integrera både långt ut åt höger och långt ut åt vänster ex.

${\int }_{-1000}^{1000}{x}^2-1dx$ då får vi en väldigt stor integral/area eftersom vi täcker in stora delar av grafen ovan.

Den allra största arean får vi om vi går ända ut till oändligheten åt båda hållen eftersom vi då täcker in hela arean under grafen.

${\int }_{-\infty }^{\infty }{x}^2-1dx$ och arean blir då oändligt stor eftersom grafen bara fortsätter och fortsätter åt båda håll och inte har något slut, även om det kanske inte syns så bra på bilden

Jaha! Tack sååå mycket! Det var en riktig bra förklaring. Jag fattar nu varför det finns ett oändlighets tecken :) Tsm