Välja gränser för att lösa dubbelintegral (eller tips på bättre lösningsstrategi)
Halloj!
Jag försöker bestämma:
där
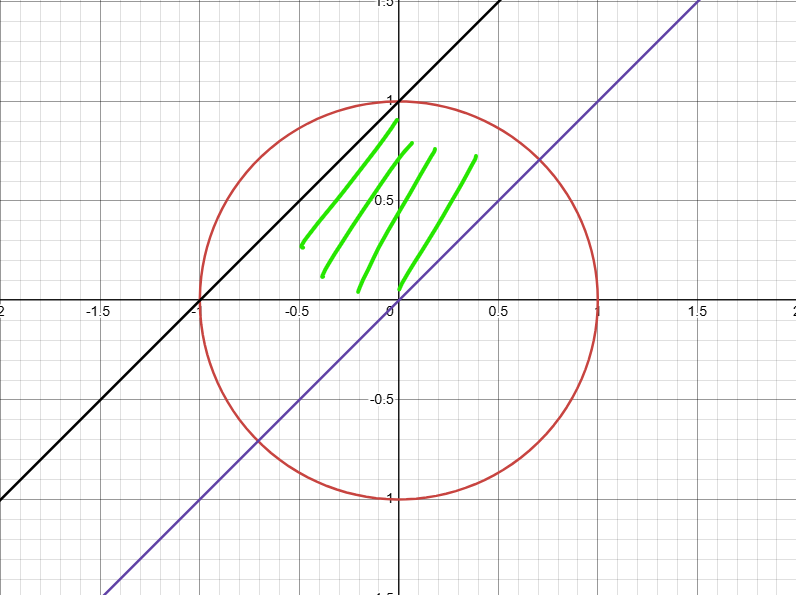
Jag har gjort en skiss i mitt block av området men laddar för enkelhetens skull upp en bild gjord i Desmos här:

Min plan är att göra ett variabelbyte till polära koordinater och dela upp området i två delar, en region där löper över till , och sedan försöka hitta på något annat klyftigt för resten av området. Jag har hittills kommit fram till:
Men det andra området blir betydligt krångligare att beskriva i polära koordinater. Jag vet inte ens om min idé är bra överhuvudtaget. Har någon förslag på hur man kan fortsätta så här eller kanske förslag på en bättre lösning?
Kan du anv en annan teknik än polära?
mellan vilka värden varierar x och hur ser y ut för varje x?
Ah, det är ju bara en linje!
Jag kan ju naturligtvis låta löpa från till och då löper från till . Så blir min "beroende variabel" och får stå i den inre integralen?
naytte skrev:Ah, det är ju bara en linje!
Jag kan ju naturligtvis låta löpa från till och då löper från till . Så blir min "beroende variabel" och får stå i den inre integralen?
Just så!
fast… x från -1 till 0
annars får du negativa sökt värde
Ska testa detta. Vet inte varför jag var så inställd på att använda pol. koordinater. Ibland fastnar man i tankespår...
Och yes, insåg det också nyss ang. ordningen för gränserna för .
Återkommer efter försök.
Jag får (om jag har räknat rätt på båda integralerna):
Kan inte riktigt avgöra om det är rimligt men det känns väldigt litet. Samtidigt ligger grafen mycket nära origo hela tiden så det kanske är rimligt ändå...

naytte skrev:Jag får (om jag har räknat rätt på båda integralerna):
Kan inte riktigt avgöra om det är rimligt men det känns väldigt litet. Samtidigt ligger grafen mycket nära origo hela tiden så det kanske är rimligt ändå...
Det är rätt svar
Okej, då var det trots allt inte så krångligt som jag rörde till det till i min hjärna!
Tack för hjälpen! :D
naytte skrev:Halloj!
Jag försöker bestämma:
där
Jag har gjort en skiss i mitt block av området men laddar för enkelhetens skull upp en bild gjord i Desmos här:
Min plan är att göra ett variabelbyte till polära koordinater och dela upp området i två delar, en region där löper över till , och sedan försöka hitta på något annat klyftigt för resten av området. Jag har hittills kommit fram till:
Men det andra området blir betydligt krångligare att beskriva i polära koordinater. Jag vet inte ens om min idé är bra överhuvudtaget. Har någon förslag på hur man kan fortsätta så här eller kanske förslag på en bättre lösning?
Jag förstår inte hur du vet att övre gränsen går till pi/2? Jag fick också att den börjar från pi/4. I min bild inkluderar jag även tredje kvadranten men du har bara skissat med grön färg området mellan första och andra kvadranten, varför är inte tredje kvadranten med?
Tillägg: 11 maj 2025 08:32
Elr nvm ska ju vara mellan 0 och 1 och y>=0 då är det första och andra kvandraten vi ska vara. Nu tror jag att jag även att jag förstår varför övre gränsen ska vara pi/2