Var gör jag fel? (Bestämning av tangent ekvation för f(x) = e^x)
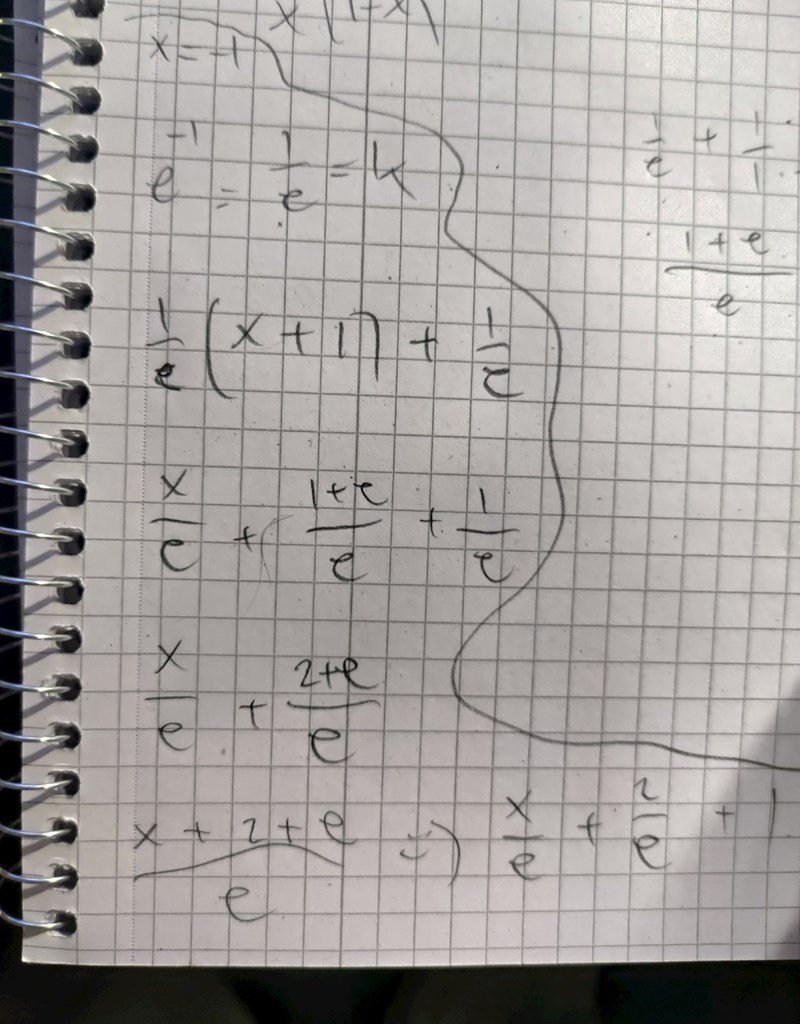
3085c) Jag får + 1 på slutet av ekvationen vilket det inte ska vara, så jag förstår inte i vilket steg jag gör fel? Kan någon hjälpa mig? 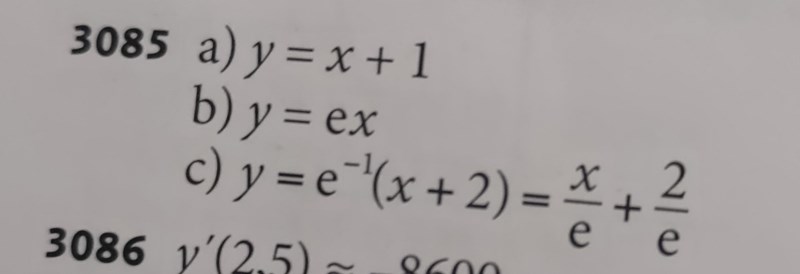
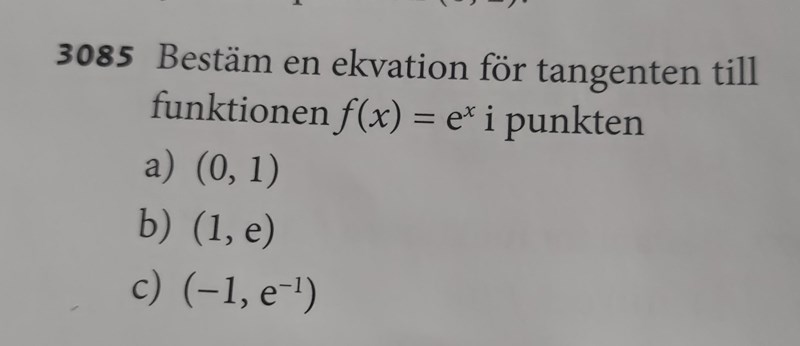
Nej, jag fattar inte vad du gör. Vilken är derivatan av x/e? Vilken är derivatan av 2/e? Vilken är derivatan av x/e + 2/e?
Smaragdalena skrev:Nej, jag fattar inte vad du gör. Vilken är derivatan av x/e? Vilken är derivatan av 2/e? Vilken är derivatan av x/e + 2/e?
Varför behöver jag göra derivata av de? Jag har gjort d/dx på e^x för att få e^x, matar in -1 som blir 1/e som är k, sen tangentens ekvation som är f'(a)(x-a)+f(a), matar in värderna i den ekvationen som blir 1/e(x+1)+1/e....
Ahhh, är det facit i översta rutan? Jag trodde att du skulle derivera det som stod efter 3085 c)!
Då har vi alltså att i punkten (-1,e-1) så är derivatan 1/e, så om vi stoppar in allting i y = kx+m får vi 1/e = (1/e)(-1)+m så m har värdet 2/e. Alltså blir det y = x/e + 2/e.
Så på översta raden skriver du att x = -1. På nästa rad konstaterar du att riktningskoefficienten är lika med 1/e. Vad är det för uttryck du har på nästa rad? Vad gör du på raden efter det? Nej, jag begriper inte vad du sysslar med.
Zerenity skrev:... sen tangentens ekvation som är f'(a)(x-a)+f(a) ...
Använd likhetstecken! Vad är ovanstående lika med?
Den räta linjens ekvation på enpunktsform är dock den smidigaste lösningen, så du är på något sätt på rätt väg. Det blir dock fel på ungefär rad 4 när du multiplicerar ut parentesen.
Dr. G skrev:Zerenity skrev:... sen tangentens ekvation som är f'(a)(x-a)+f(a) ...Använd likhetstecken! Vad är ovanstående lika med?
Den räta linjens ekvation på enpunktsform är dock den smidigaste lösningen, så du är på något sätt på rätt väg. Det blir dock fel på ungefär rad 4 när du multiplicerar ut parentesen.
JAHAAAAAAAAAAA........ då har jag hittat felet, tack så mycket :) Och ekvationen är lika med t(x) brukar jag skriva, typ funktion t som är tangentens ekvation
Dr.G skrev:
Den räta linjens ekvation på enpunktsform är dock den smidigaste lösningen
Jag håller inte med, jag tycker det är enklare att sätta in i y = kx+m som jag visade, men det betyder bara att våra hjärnor är kopplade på lite olika vis.




