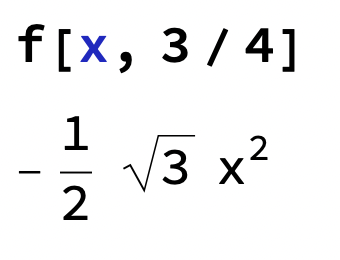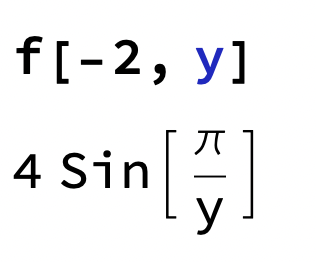Var ska jag börja med dessa?

Den första kräver i alla fall bara att man vet vad partiell derivata är. Jag tror endast att man behöver första ordningen.

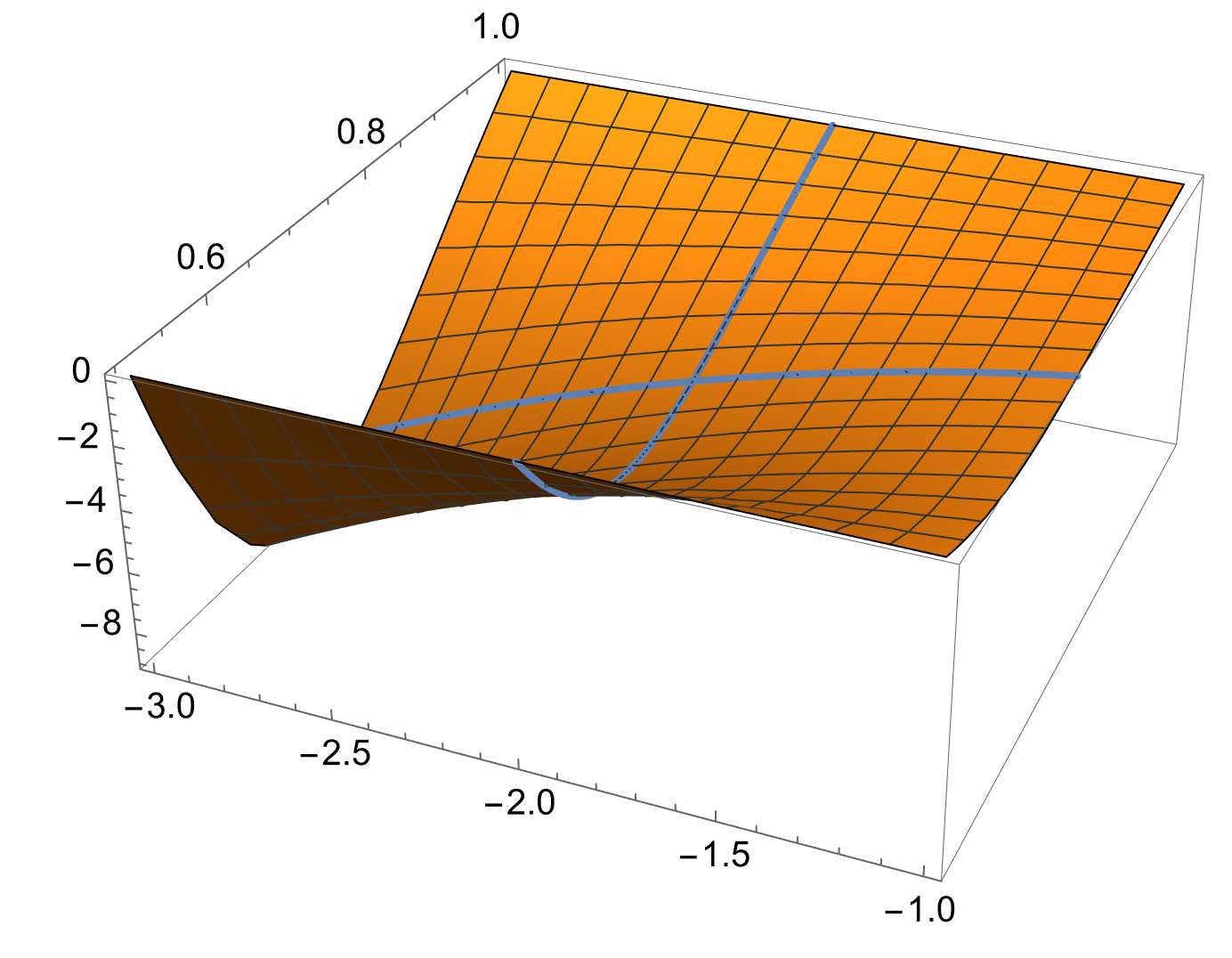
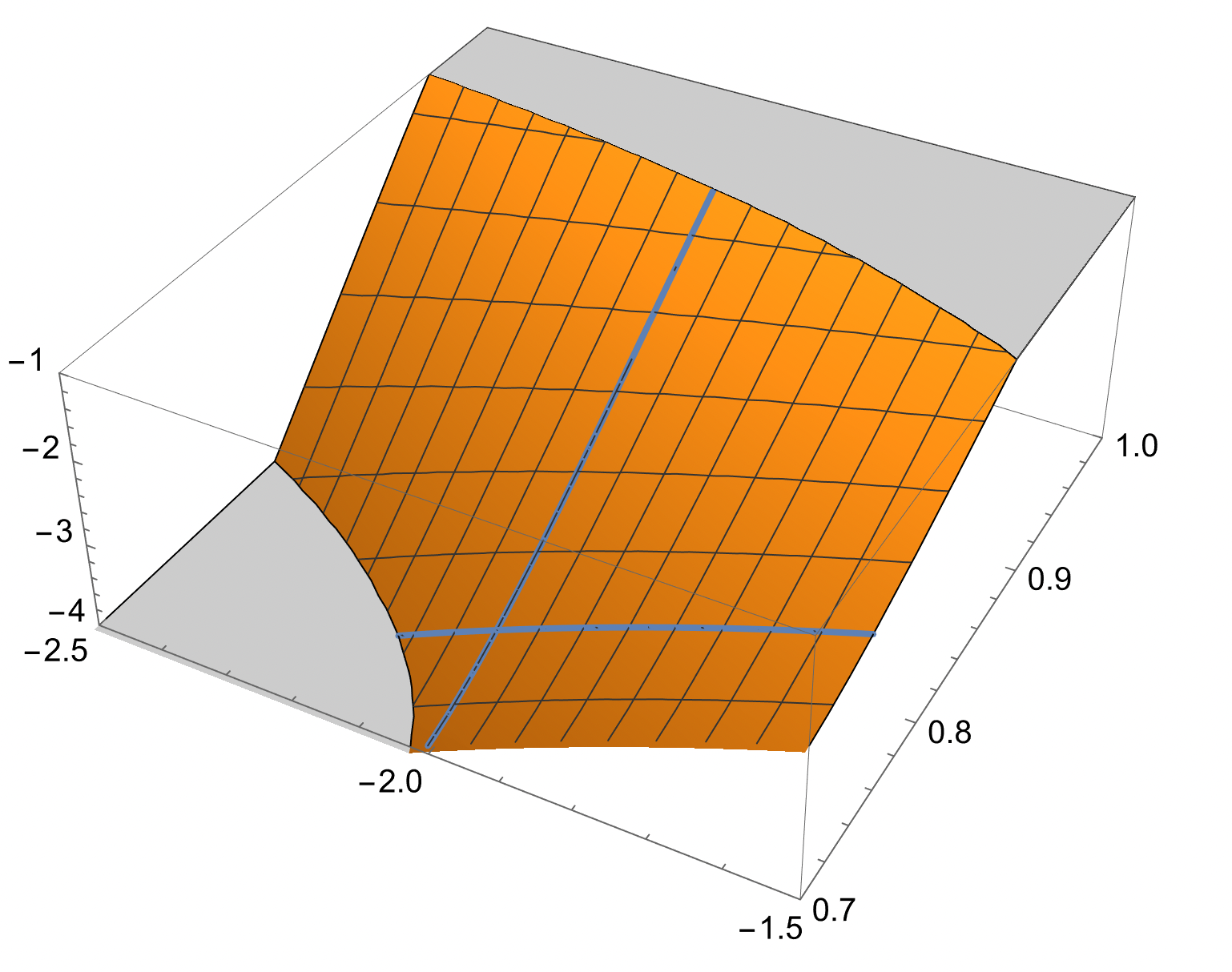
Ja, #1 är inte så svår. Här är en bild som visar på situationen

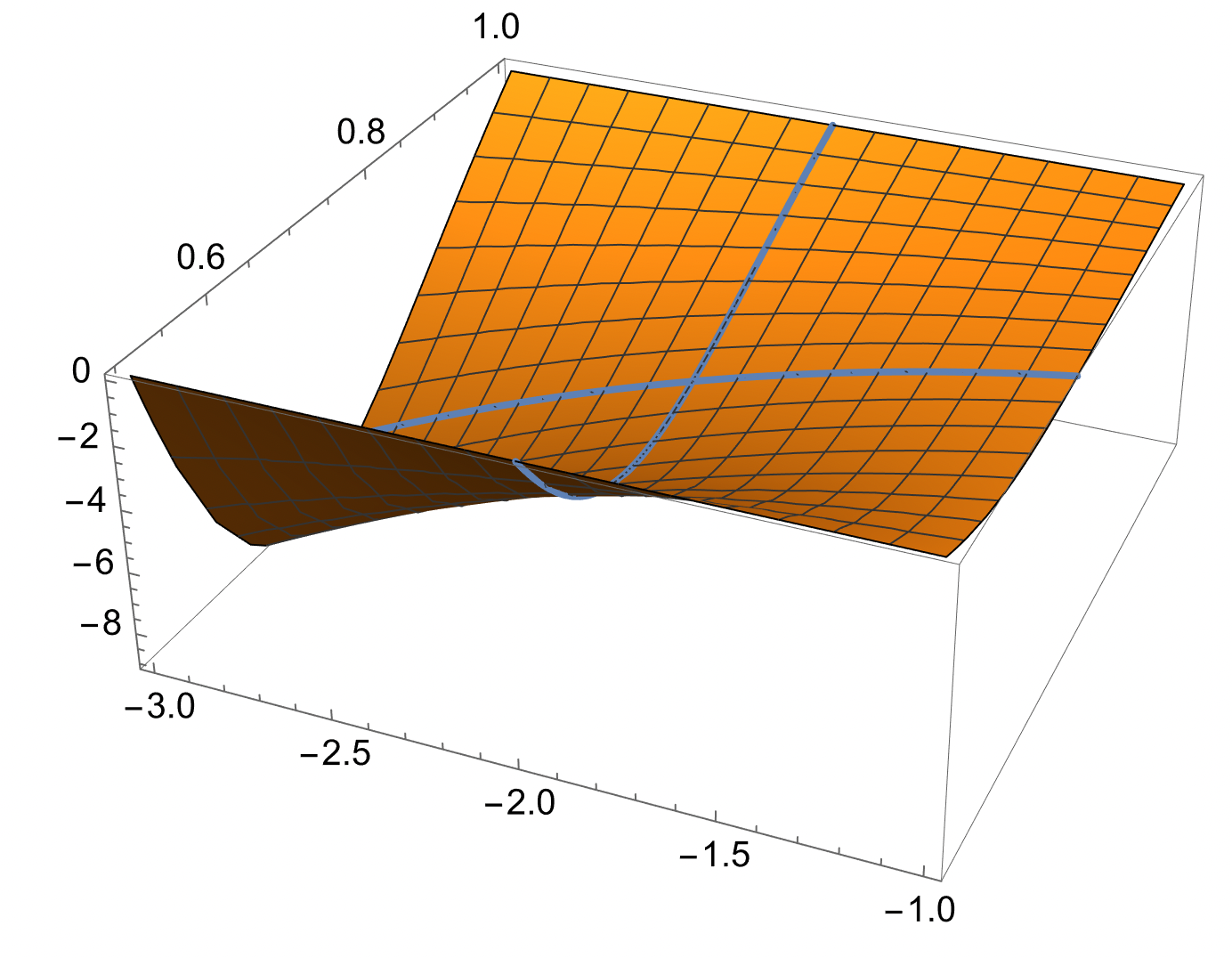
Trinity2 skrev:

Ja, #1 är inte så svår. Här är en bild som visar på situationen

dafu.... how did you do that :O

Sykey skrev:

Trinity2 skrev:

Ja, #1 är inte så svår. Här är en bild som visar på situationen

 

dafu.... how did you do that :O

Kanske finns motsv. möjlighet i Geogebra. Desmos tror jag kan detta.

Det brukar finnas lösningar till ex-tentor på nätet, kanske på utbildningens hemsida t.o.m. Kolla där.

Trinity2 skrev:

Det brukar finnas lösningar till ex-tentor på nätet, kanske på utbildningens hemsida t.o.m. Kolla där.

Ahh kanske men detta är inte tenta uppgifter tror jag. Det är en study coach som delar ut dessa uppgifter till oss (utan facit eller lösning). 

1. Derivera f map x och map y

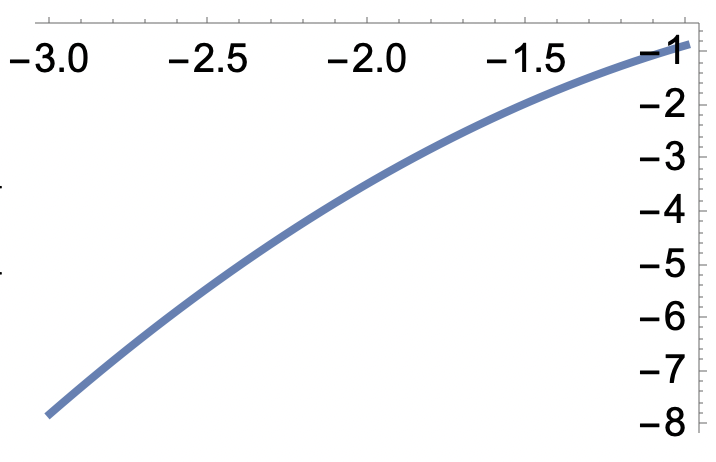
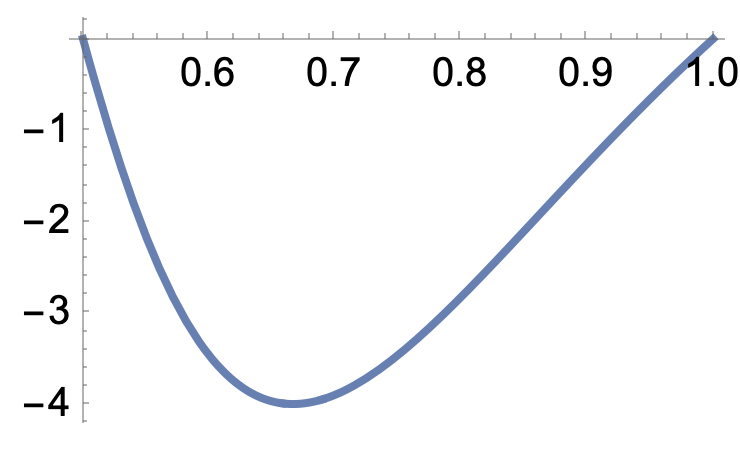
a) Fixera y=3/4 och studera när x varierar, t.ex. på (-3,-1)

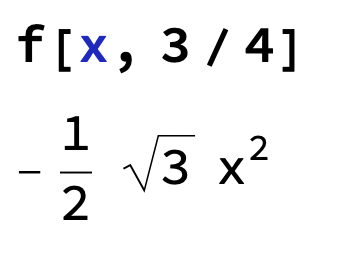
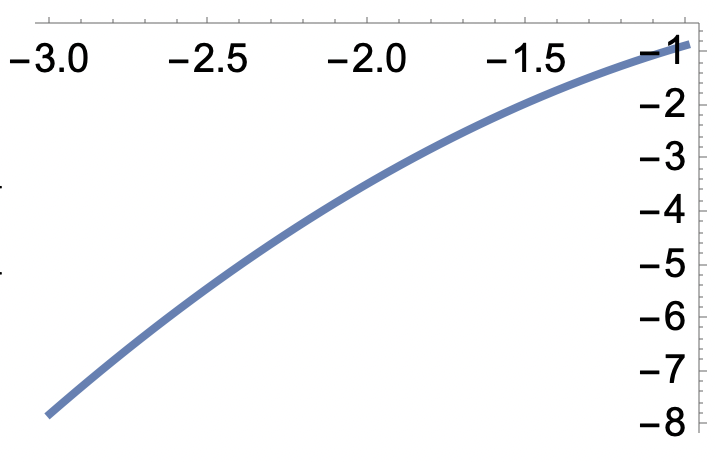
b) Gör samma sak fast med fixt x

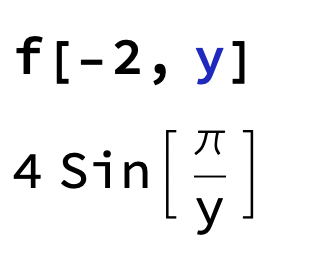
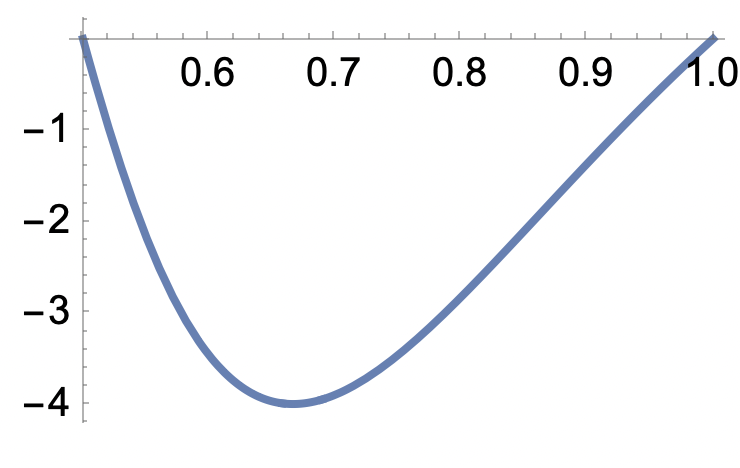
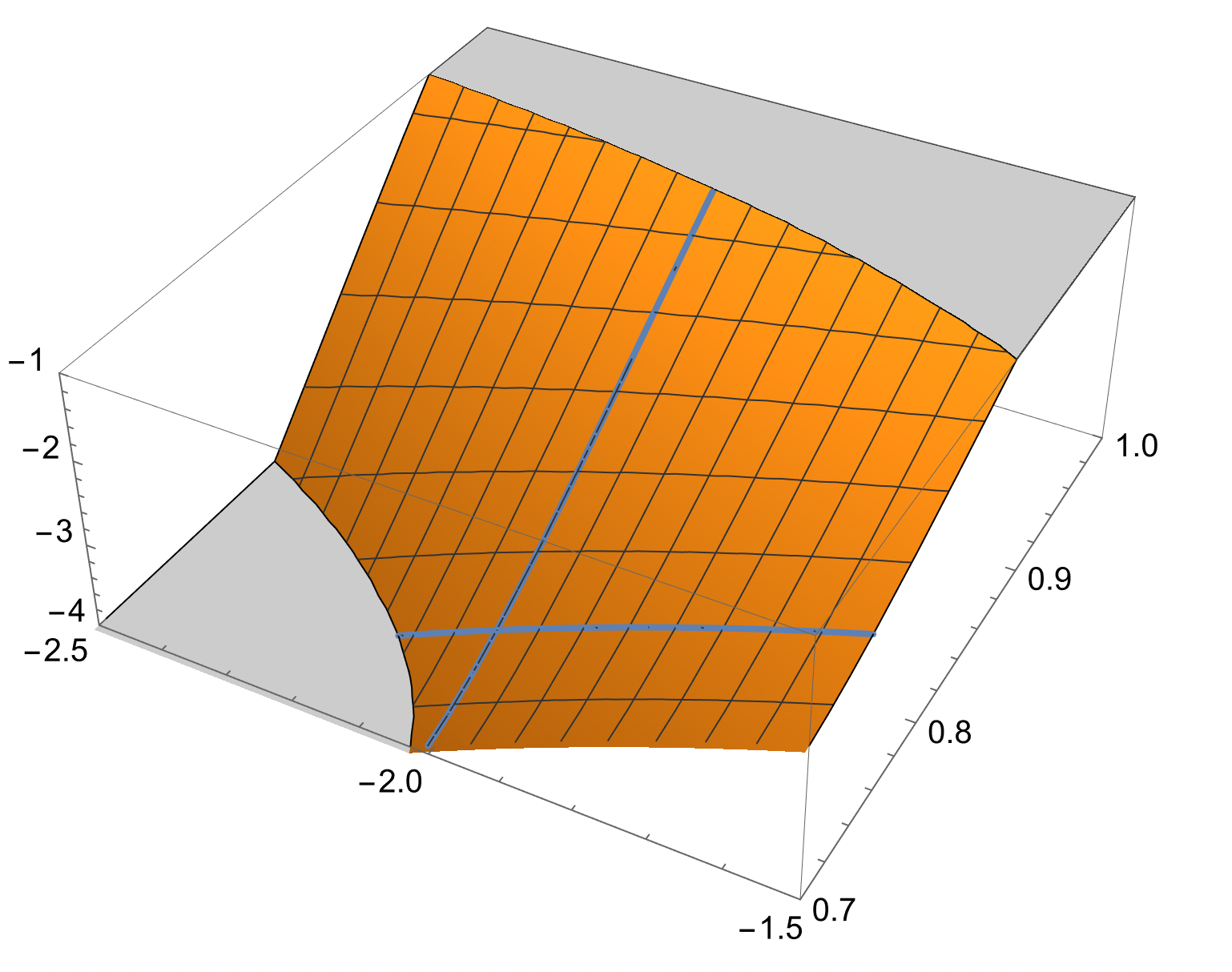
Vi ser att den växer i båda "kors-riktningar" i punkten (-2,3/4)

Trinity2 skrev:

1. Derivera f map x och map y

a) Fixera y=3/4 och studera när x varierar, t.ex. på (-3,-1)

b) Gör samma sak fast med fixt x

Vi ser att den växer i båda "kors-riktningar" i punkten (-2,3/4)

Sorry men hur fick du fram det värdet på a)? Deriverade du? Sin försvann helt

Edit: Lite osäker på om derivering ens skedde.

Fixerade y=3/4 

Fick (på funktion f) sin($\frac{\mathrm{\pi }}{3}+\mathrm{\pi }$)= sin($\mathrm{\pi }$/3)*cos(π) + 0 = -$\frac{\sqrt{3}}{2}$

-->   -$\frac{\sqrt{3}}{2}{x}^2$... okej alltså precis som du gjorde men

jag fattar inte varför vi bytte till en annan punkt (-3,-1), de frågar ju om punkten (2, 3/4)... om x varierar så är vi inte längre i samma punkt? Liksom en punkt på denna bestämda grafen har en viss karaktär oavsett? Jag fattar inte varför vi ska variera x och vad det innebär.