Varför är rörelsemängdsmomentet för klossen mvR?

Rörelsemängd mv, momentarm R.

Men hur kan momentarmen vara $R$?

Jag har svårt att förstå hur klossen ens kan ha rörelsemängdsmoment runt $O$ eftersom den inte roterar överhuvudtaget, den faller väl bara rakt ned?

Det är rörelsemängdsmomentet runt O vi söker.

Om vi tänker oss systemet utan vikten, så kan vi bromsa skivan genom att applicera ett vridmoment i O.

Har du spänt hjulmuttrar med en momentnyckel någon gång? Hur man än tar i, får man bara ett visst vridmoment.

Lägg till vikten och tänk dig att du applicerar samma moment. Ju längre hävarm R, desto svårare att bromsa hela systemet.

Jag förstår att om vi skulle tillämpa en kraft med mot $R$ vinkelrät komponent:

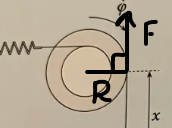
Skulle vi kunna få hjulet att stanna.

Men jag ser tyvärr fortfarande inte riktigt hur vikten kan ha ett vridmoment (eller rörelsemängdsmoment). Den tillämpar väl ingen kraft direkt på hjulet?

Hjulet börjar ju uppenbarligen att snurra men jag får inte ihop varför. Vilket vridmoment får det att börja snurra?

Om man ersätter den där vikten med samma massa m fördelad på en tunn ring längs hjulets kant får vi ett ekvivalent system där massan m fortfarande har samma tangentialhastighet och samma hävarm R.

Är du med på den ekvivalensen? Om du räknar fram rotationströghetsmomentet för ringen (ganska lätt) kommer du att få samma slutresultat eftersom systemen är ekvivalenta.

Menar du att vi skulle skapa ett ekvivalent system på formen:

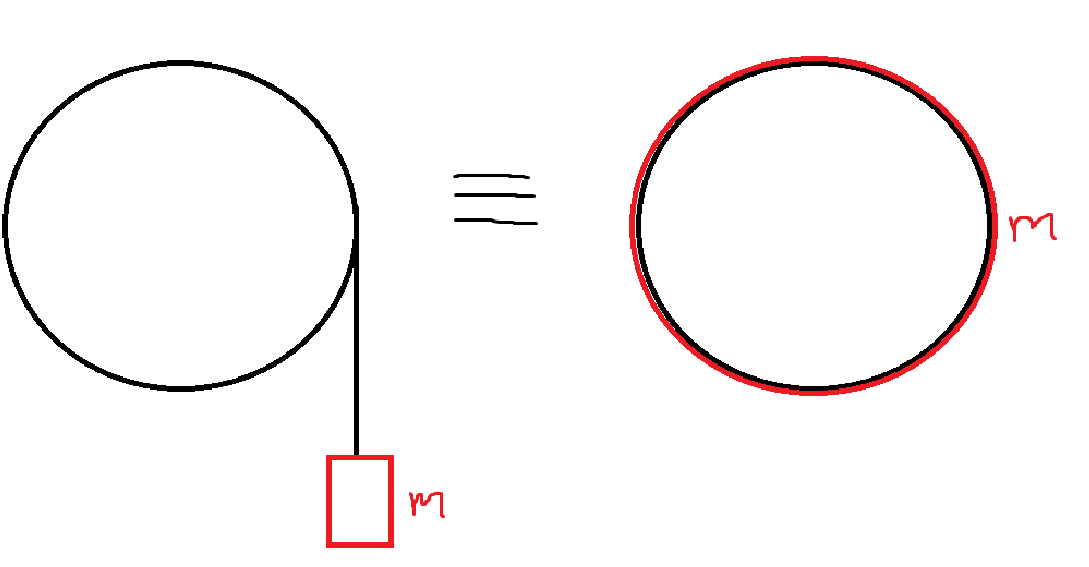
Ja. Man ser direkt att de är ekvivalenta enligt definitionen

https://sv.wikipedia.org/wiki/R%C3%B6relsem%C3%A4ngdsmoment

Ekvivalenta just för den fråga du ställde, naturligtvis inte för hela uppgift 10.1.4

Jag förstår inte hur vi kan ha en ekvivalens här. Vi har ju fundamentalt ändrat systemuppställningen, även med avseende på endast min fråga.

I uttrycket $\mathbf{L} = \mathbf{R} \times m\mathbf{v}$

ska väl $\mathbf{R}$ vara lägesvektorn från rotationsaxeln $O$ till partikeln (massan i vårt fall)?

naytte skrev:

I uttrycket $\mathbf{L} = \mathbf{R} \times m\mathbf{v}$

ska väl $\mathbf{R}$ vara lägesvektorn från rotationsaxeln $O$ till partikeln (massan i vårt fall)?

Jo, men det är en kryssprodukt. Lodräta komponenten av lägesvektorn ger bidraget noll.

Jaha, så sant!

Så den enda komponenten som är vinkelrät är den vågräta komponenten och den sträckan är $R$?

Javisst.

Ah, då är jag med!

Börjar bli trött nu... Det känns så uppenbart nu.

Tack för hjälpen och tålamodet!